SVM用于线性回归
SVM用于线性回归
方法分析
在样本数据集()中,不是简单的离散值,而是连续值。如在线性回归中,预测房价。与线性回归类型,目标函数是正则平方误差函数:
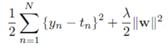
在SVM回归算法中,目的是训练出超平面,采用作为预测值。为了获得稀疏解,即计算超平面参数w,b不依靠所有样本数据,而是部分数据(如在SVM分类算法中,支持向量的定义),采用误差函数
误差函数定义为,如果预测值与真实值的差值小于阈值将不对此样本做惩罚,若超出阈值,惩罚量为。
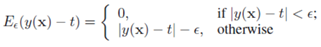
下图为误差函数与平方误差函数的图形
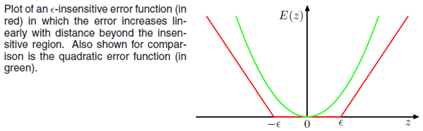
目标函数
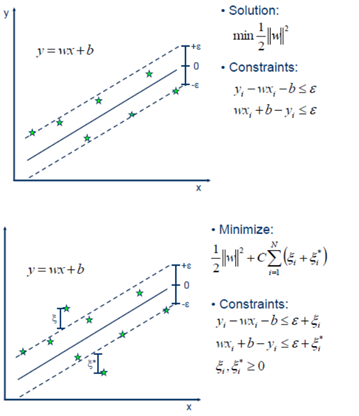
观察上述的误差函数的形式,可以看到,实际形成了一个类似管道的样子,在管道中样本点,不做惩罚,所以被称为,如下图阴影红色部分
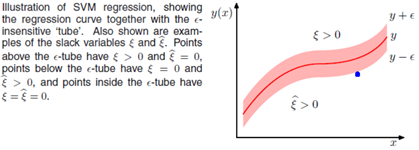
用替代平方误差项,因此可以定义最小化误差函数作为优化目标:
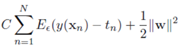
由于上述目标函数含有绝对值项不可微。我们可以转化成一个约束优化问题,常用的方法是为每一个样本数据定义两个松弛变量,表示度量与的距离。
如上图所示:
当样本点真实值位于管道上方时,写成表达式:时,
当样本点真实值位于管道下方时,写成表达式:时,
因此使得每个样本点位于管道内部的条件为:
当位于管道上方时,,有
当位于管道下方时,,有
误差函数可以写成为一个凸二次优化问题:
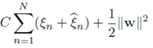
约束条件为:

写成拉格朗日函数:

对偶问题
上述问题为极小极大问题
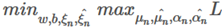
与SVM分类分析方法一样,改写成对偶问题
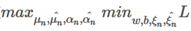
首先求偏导数




超平面计算

Support Vector Machine - Regression (SVR)
Support Vector Machine can also be used as a regression method, maintaining all the main features that characterize the algorithm (maximal margin). The Support Vector Regression (SVR) uses the same principles as the SVM for classification, with only a few minor differences. First of all, because output is a real number it becomes very difficult to predict the information at hand, which has infinite possibilities. In the case of regression, a margin of tolerance (epsilon) is set in approximation to the SVM which would have already requested from the problem. But besides this fact, there is also a more complicated reason, the algorithm is more complicated therefore to be taken in consideration. However, the main idea is always the same: to minimize error, individualizing the hyperplane which maximizes the margin, keeping in mind that part of the error is tolerated.
Linear SVR
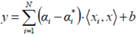
Non-linear SVR
The kernel functions transform the data into a higher dimensional feature space to make it possible to perfom the linear separation

Kernel functions





