最小生成树

最小生成树

通用最小生成树

    假定有一个连通无向图G=(V,E)和权重函数,我们希望找出图G的一颗最小生成树，Kruskal和Prim算法都是使用贪心策略来解决这个问题，但它们使用贪心策略的方式却有所不同。

    这个贪心策略可以由下面的通用方法来表述。该通用方法在每个时刻生长最小生成树的一条边，并在整个策略的实施过程中，管理一个遵守下述循环不变式的边集合A：

    在每遍循环之前，A是某棵树最小生成树的一个子集。

    在每一步，我们要做的事情是选择一条边（u,v），将其加入到集合A中，使得A不违反循环不变式，即也是某棵最小生成树的子集。由于我们可以安全地将这种边加入到集合A而不破坏A的循环不变式，因此称这样的边为集合A的安全边。

使用循环不变式的方式如下：

初始化：在算法第1行之后，集合A直接满足循环不变式。

保持：算法2-4行的循环通过只加入安全边来维持循环不变式。

终止：所有加入到集合A中的边都属于某颗最小生成树，因此，算法第5行返回的集合A必然是一颗最小生成树。

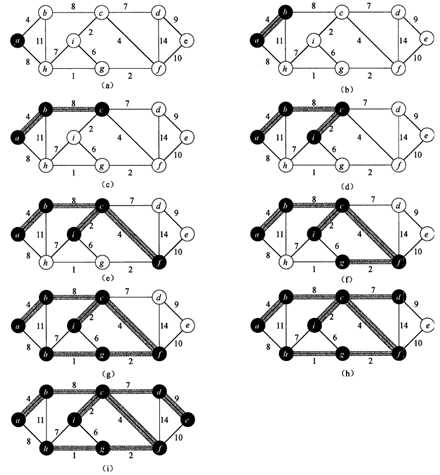
Kruskal算法

kruaskal算法找到安全边的方法是，在所有连接森林中两颗不同树的边里面，找到权重最小的边（u,v）。

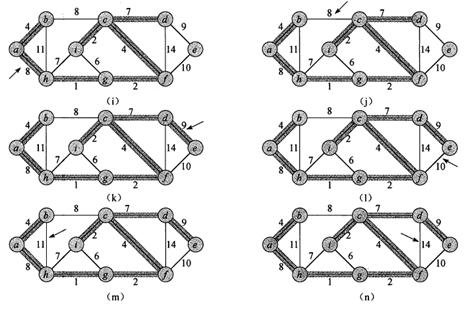
Prim算法

与Kruskal算法类似，Prim算法也是通用最小生成树的一个特例。Prim算法的工作原理与Dijkstra的最短路径算法相似。Prim算法所具有的一个性质是集合A中边总是构成一棵树。这颗树从一个任意的根节点r开始，一直长大到覆盖V中的所有结点时为止。算法每一步在连接集合A和A之外的节点所有边中，选择一条轻量级边加入到A中。这条规则所加入的边都是对A安全的边。因此，当算法终止时，A中的边形成一棵最小生成树。本策略也属于贪心策略，因为每一步加入的边都必须是使树的总权重增加量最小的边。

    为了有效实现Prim算法，需要一种快速的方法来选择一条新的边，以便加入到由集合A中边所构成的树里。上面的伪代码中，连通图G和最小生成树的根节点r将作为算法的输入。在算法的执行过程中，所有不在树A中的结点都存放在一个基于key属性的最小优先队列Q中。对于每个节点v，属性v.key保存的是连接v和树中节点的所有边中最小边的权重。我们规定如果不存在这样的边，则。属性给出的是节点v在树中的父节点Prim算法将GENERIC-MST中的结合A维持在的状态下。

    当Prim算法终止时，最小优先队列Q将为空，而G的最小生成树A则是：