Leetcode 684.冗余连接

冗余连接

在本问题中, 树指的是一个连通且无环的无向图。

输入一个图，该图由一个有着N个节点 (节点值不重复1, 2, ..., N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ，满足 u < v，表示连接顶点u 和v的无向图的边。

返回一条可以删去的边，使得结果图是一个有着N个节点的树。如果有多个答案，则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。

示例 1：

输入: [[1,2], [1,3], [2,3]]

输出: [2,3]

解释: 给定的无向图为:

 

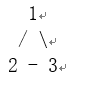
示例 2：

输入: [[1,2], [2,3], [3,4], [1,4], [1,5]]

输出: [1,4]

解释: 给定的无向图为:

 

注意:

• 输入的二维数组大小在 3 到 1000。
• 二维数组中的整数在1到N之间，其中N是输入数组的大小。

更新(2017-09-26):
我们已经重新检查了问题描述及测试用例，明确图是无向 图。对于有向图详见冗余连接II。对于造成任何不便，我们深感歉意。

 

思路

并查集，new一个数组，用来保存各个节点的根节点（这里（1,2）是说2是1的根节点），遍历edges数组时，查找两个数组的根节点是否相等，相等则证明有环，则返回当前数组。

 

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int[] nums = new int[2000];

        for(int[] i : edges){
            int root1 = find(i[0],nums);
            int root2 = find(i[1],nums);
            if (root1 == root2)
                return i;
            else {
                nums[root1] = root2;
            }
        }
        return null;

    }

    public static int find(int x, int[] nums){
        while (nums[x] != 0){
            x = nums[x];
        }
        return x;
    }
}