Leetcode 391.完美矩形
完美矩形
我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。
每个矩形用左下角的点和右上角的点的坐标来表示。例如, 一个单位正方形可以表示为 [1,1,2,2]。 ( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为 (2, 2) )。

示例 1:
rectangles = [
[1,1,3,3],
[3,1,4,2],
[3,2,4,4],
[1,3,2,4],
[2,3,3,4]
]
返回 true。5个矩形一起可以精确地覆盖一个矩形区域。
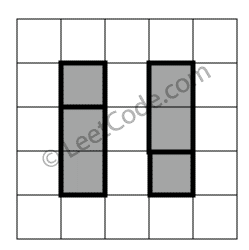
示例 2:
rectangles = [
[1,1,2,3],
[1,3,2,4],
[3,1,4,2],
[3,2,4,4]
]
返回 false。两个矩形之间有间隔,无法覆盖成一个矩形。
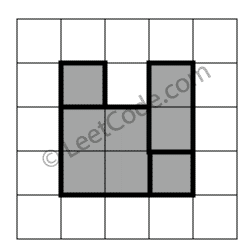
示例 3:
rectangles = [
[1,1,3,3],
[3,1,4,2],
[1,3,2,4],
[3,2,4,4]
]
返回 false。图形顶端留有间隔,无法覆盖成一个矩形。
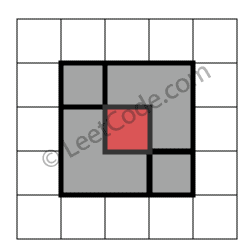
示例 4:
rectangles = [
[1,1,3,3],
[3,1,4,2],
[1,3,2,4],
[2,2,4,4]
]
返回 false。因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
核心思想就是:能够正好围成一个矩形的情况就是:
有且只有:
- 最左下 最左上 最右下 最右上 的四个点只出现过一次,其他肯定是成对出现的(保证完全覆盖)
- 上面四个点围成的面积,正好等于所有子矩形的面积之和(保证不重复)
1 import java.util.HashSet; 2 3 /** * 核心思想就是:能够正好围成一个矩形的情况就是: 4 * 有且只有: 5 * - 最左下 最左上 最右下 最右上 的四个点只出现过一次,其他肯定是成对出现的(保证完全覆盖) 6 * - 上面四个点围成的面积,正好等于所有子矩形的面积之和(保证不重复) 7 * Created by MebiuW on 16/8/29. */ 8 9 public class Solution{ 10 public boolean isRectangleCover(int[][] rectangles){ 11 int left=Integer.MAX_VALUE; 12 int right=Integer.MIN_VALUE; 13 int top=Integer.MIN_VALUE; 14 int bottom=Integer.MAX_VALUE; 15 int n=rectangles.length; 16 HashSet<String> flags=new HashSet<String>(); 17 int totalArea=0; 18 for(int i=0;i<n;i++){ 19 left=Math.min(left,rectangles[i][0]); 20 bottom=Math.min(bottom,rectangles[i][1]); 21 right=Math.max(right,rectangles[i][2]); 22 top=Math.max(top,rectangles[i][3]); 23 totalArea+=(rectangles[i][3]-rectangles[i][1])*(rectangles[i][2]-rectangles[i][0]); 24 String pointLT=rectangles[i][0]+" "+rectangles[i][3]; 25 String pointLB=rectangles[i][0]+" "+rectangles[i][1]; 26 String pointRT=rectangles[i][2]+" "+rectangles[i][3]; 27 String pointRB=rectangles[i][2]+" "+rectangles[i][1]; 28 if(!flags.contains(pointLT)) flags.add(pointLT); 29 else flags.remove(pointLT); 30 if(!flags.contains(pointLB)) flags.add(pointLB); 31 else flags.remove(pointLB); 32 if(!flags.remove(pointRT)) flags.add(pointRT); 33 else flags.remove(pointRT); 34 if(!flags.contains(pointRB)) flags.add(pointRB); 35 else flags.remove(pointRB); 36 } 37 if(flags.size()==4&&flags.contains(left+" "+top) 38 &&flags.contains(left+" "+bottom) 39 &&flags.contains(right+" "+bottom) 40 &&flags.contains(right+" "+top)){ 41 return totalArea==(right-left)*(top-bottom); 42 } 43 return false; 44 } 45 }


