Leetcode 218.天际线问题

天际线问题

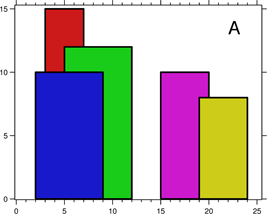
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在，假设您获得了城市风光照片（图A）上显示的所有建筑物的位置和高度，请编写一个程序以输出由这些建筑物形成的天际线（图B）。

每个建筑物的几何信息用三元组 [Li，Ri，Hi] 表示，其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标，Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。

例如，图A中所有建筑物的尺寸记录为：[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。

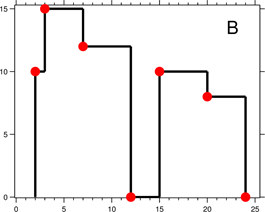
输出是以 [ [x1,y1], [x2, y2], [x3, y3], ... ] 格式的"关键点"（图B中的红点）的列表，它们唯一地定义了天际线。关键点是水平线段的左端点。请注意，最右侧建筑物的最后一个关键点仅用于标记天际线的终点，并始终为零高度。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

例如，图B中的天际线应该表示为：[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。

说明:

• 任何输入列表中的建筑物数量保证在 [0, 10000] 范围内。
• 输入列表已经按升序排列在左边的 x 位置 Li 。
• 输出列表必须按 x 位排序。
• 输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]

思路

如果按照一个矩形一个矩形来处理将会非常麻烦，我们可以把这些矩形拆成两个点，一个左上顶点，一个右上顶点。将所有顶点按照横坐标排序后，我们开始遍历这些点。遍历时，通过一个堆来得知当前图形的最高位置。堆顶是所有顶点中最高的点，只要这个点没被移出堆，说明这个最高的矩形还没结束。对于左顶点，我们将其加入堆中。对于右顶点，我们找出堆中其相应的左顶点，然后移出这个左顶点，同时也意味这这个矩形的结束。具体代码中，为了在排序后的顶点列表中区分左右顶点，左顶点的值是正数，而右顶点值则存的是负数。

注意

• 堆中先加入一个零点高度，帮助我们在只有最矮的建筑物时选择最低值

复杂度

时间 O(NlogN) 空间 O(N)

 

public class Solution {
    public List<int[]> getSkyline(int[][] buildings) {
        List<int[]> result = new ArrayList<>();
        List<int[]> height = new ArrayList<>();
        // 拆解矩形，构建顶点的列表
        for(int[] b:buildings) {
            // 左顶点存为负数
            height.add(new int[]{b[0], -b[2]});
            // 右顶点存为正数
            height.add(new int[]{b[1], b[2]});
        }
        // 根据横坐标对列表排序，相同横坐标的点纵坐标小的排在前面
        Collections.sort(height, new Comparator<int[]>(){
            public int compare(int[] a, int[] b){
                if(a[0] != b[0]){
                    return a[0] - b[0];
                } else {
                    return a[1] - b[1];
                }
            }
        });
        // 构建堆，按照纵坐标来判断大小
        Queue<Integer> pq = new PriorityQueue<Integer>(11, new Comparator<Integer>(){
            public int compare(Integer i1, Integer i2){
                return i2 - i1;
            }
        });
        // 将地平线值9先加入堆中
        pq.offer(0);
        // prev用于记录上次keypoint的高度
        int prev = 0;
        for(int[] h:height) {
            // 将左顶点加入堆中
            if(h[1] < 0) {
                pq.offer(-h[1]);
            } else {
                // 将右顶点对应的左顶点移去
                pq.remove(h[1]);
            }
            int cur = pq.peek();
            // 如果堆的新顶部和上个keypoint高度不一样，则加入一个新的keypoint
            if(prev != cur) {
                result.add(new int[]{h[0], cur});
                prev = cur;
            }
        }
        return result;
    }
}