数据流

数据流

引子

编译器后端会对前端生成的中间代码做很多优化，也就是在保证程序语义不变的前提下，提高程序执行的效率或减少代码size等优化目目标。优化需要依靠代码分析给出的"指导信息"来相应地改进代码，而代码分析中最重要的就是数据流分析。另外数据流分析是程序静态分析的基础。所以掌握数据流分析对编译后端极为重要。

何为数据流分析

数据流分析指的是一组用来获取有关数据如何沿着程序执行路径流动的相关信息的技术

数据分析的目的是提供一个过程（或一大段程序）如何操作其数据的全局信息。

从上面的表述中，我们可以看到数据流分析通过静态代码来"推断"程序执行的相关信息，数据流分析并不真正执行程序。虽然数据流分析和符号执行在某些方面比较相似，但还是两种不同的概念，更确切的说数据流分析是符号执行的基础。

数据流分析和符号执行从某些方面都很相似，例如符号执行有程序点（ProgramPoint）的概念，并且在当前程序存储着程序运行到此刻的所有状态和值信息（一般情况下不会维护历史程序点的信息，开销太大）。数据流分析中也有程序点的概念，程序点存储着数据流信息。两者都是在CFG（Control Flow Graph）图的基础上，进行的分析。Clang的静态分析示意图如下所示，Clang会时刻维护符号执行当前的状态和内存信息。从这一点上看，符号执行和虚拟机更为相似。

但数据流分析和符号执行还是不同的，虽然都有程序点，但程序点存储的信息却是两个不同的概念。数据流分析中程序点存储的是数据流值，这些数据流值是和具体的数据流问题相关的，有可能是当前程序点的定值信息，也可能是可用表达式信息，这些信息标识这该程序内含的一些属性。符号执行中程序点存储的是程序符号执行到此处的所有状态和值信息，这些信息和程序运行更为相关。

而且两者的分析方法也不同，符号执行是单次执行，而数据流分析大多采用迭代分析的框架，然后在迭代分析的过程中不断更新程序点的数据流信息，最终得到比精确解更小（更保守）的解。但为了进行更为激进的优化，要求数据流分析在保证保守的同时又尽可能是激进的。

数据流抽象

在前面的文章中我们也提到过，程序的执行可以看作是程序状态的一系列转换。程序状态是由程序中所有的变量的值以及运行时栈帧上的相关值组成。程序语句对应着转换函数，将前一个程序点的输入程序转换到下一个程序点的新的输出状态。

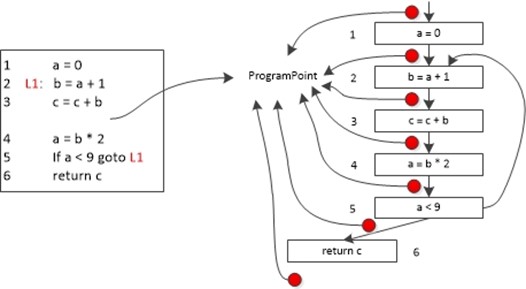
上图所示中的红点表示的就是程序点，数据流转换函数就是作用在程序点上的状态，并沿着程序路劲一步步进行的。其实这个过程就是一个自动机，抽象出的自动机如下所示。程序点代表自动机中的一个节点，程序语句或者说是转换函数代表自动机中的一条边。一般来说，一个程序有无穷多条可能的执行路径，执行路径的长度并没有上届（例如死循环）。程序分析可以推断出各个程序点的程序状态（有穷的特性集合），当然很少有哪种数据流分析会用到所有的数据流信息，一般只是提取出感兴趣的特性集合进行分析。

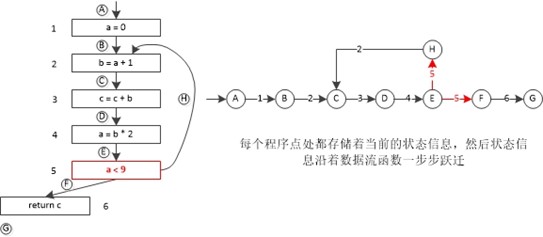
我们考虑的多数数据流分析问题关注的是各种程序对象（常数，变量，定值，表达式等）的集合，以及在过程内任意一点这些对对象的什么集合是合法的有关判断。另外在数据流分析中，一般是会忽略掉路径条件判断的，也就是说默认所有路径都是可达（这种近似是正确且有效，现在我还没有找到忽略条件也能保证数据流分析正确性的证明！），在程序分析中忽略掉程序控制条件，所以核心部分就是状态数据如何变化了，也就是数据流分析。

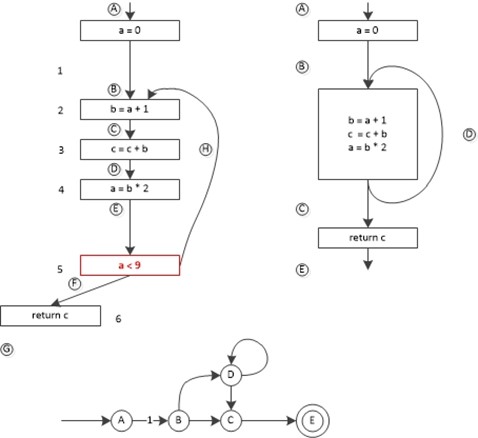
我们虽然可以对过程的控制流图进行数据流分析，但通常更为有效的做法是将它分解为局部数据流分析和全局数据流分析，局部数据流分析针对每一个基本块进行，全局数据流分析针对控制流图进行分析，其实就是一个粒度问题。我们可以将同一个基本块内的各个语句的作用综合起来和合成整一个基本快的作用。例如我们可以将上面的自动机改造为基于基本块的形式，如下图所示：

数据流分析模式

在数据流分析中，程序点一般和数据流值（data-flow value）关联起来，注意这个数据流值不是程序中变量的值。"这个值是在该点可能观察到的所有程序状态的集合的抽象表示"，这句话说起来有点绕口，每个数据流分析问题都有其对应的值域，每个程点的数据流值都是该值域的子集。比如，到达定值的数据流值的域是程序的定值集合的所有子集的集合。某个数据流值是一个定值的集合，数据流分析的目的就是推导出所有程序点与其对应的到达定值的集合。

一个定值是对某个变量的复制。可能沿着某条路径到达某个程序点的定值称为到达定值（reaching definition）

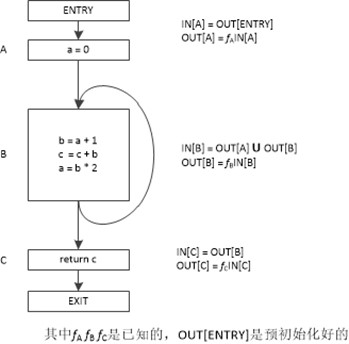
我们把每个语句s之前和之后的数据流值分别记为IN[s]和OUT[s]。数据流问题就是对一组约束求解，得到所有IN[s]和OUT[s]的结果。

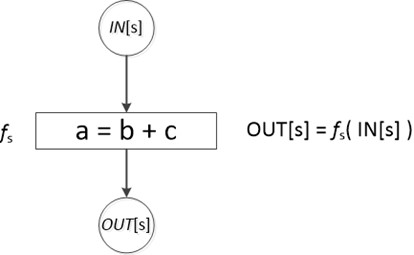
每个语句都约束了该语句之前程序状态和之后程序状态的关系，也就是说语句s限定了IN[s]和OUT[s]之间的关系。整个程序就是由无穷个这样的约束构成的。数据流问题(data-flow problem)就是对这一组约束求解，另外约束不仅有语义（传递函数）上的约束，更有基于控制流的约束。

传递函数

在一个语句之前和之后的数据流值受该语句语义道德约束，也就是程序语句前后程序点的数据流值受该语句语义的约束，这种约束关系称为传递函数（transfer function）。

传递函数有两种风格：数据流信息可能沿着执行路径前向传播，或者沿着程序路径逆向流动，相应就有前向（forward）数据流问题和后项（backward）数据流问题。

大部分人刚接触到后向数据流问题时会比较困惑，数据流值怎么会依赖于后面的数据流值信息呢。其实这是由于有些人还是对于数据流值的概念不是很理解去，将数据流值简单的归结于变量的值，如果这么对比的话，就会出现矛盾。

对于前向数据流问题，一个程序语句S的传递函数以语句前程序点的数据流值作为输入，并产生出语句之后程序点对应的新数据流值。例如到达定值就是前向数据流问题。

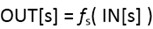
对于后向数据流问题，一个程序语句s的传递函数以及语句后的程序点的数据流值作为输入，变换为成语句之前程序点的新数据流值。例如活变量分析就是后向数据流问题。

控制流约束

第二组关于数据流值的约束是从控制流中得到的，基本块内都是顺序执行，没有控制流的约束。但是基本块之间有相应的控制流约束，例如一个基本块的最后一个语句和后继基本块的第一个语句之间地约束，这些约束比较复杂。

基本块上的数据流模式

前面我们已经提到过程序语句的约束分为两种，基于程序语句语义的约束和基于控制流的约束。基本块之间的约束都是基于控制流的约束，由于基本块内没有分支，所以我们可以基于整个基本块来描述基于块对于数据流值的约束，而不是基于程序语句（前面也提到过，我们可以使用局部数据流和全局数据流分析结合更加高效）。我们以基本块为最小单位来研究基本块上的数据流模式。

基本块的传递函数和基本块内程序语句所表示的传递函数之间的关系如上图所示。那么基本块之间的约束是如何的呢？如下图所示。

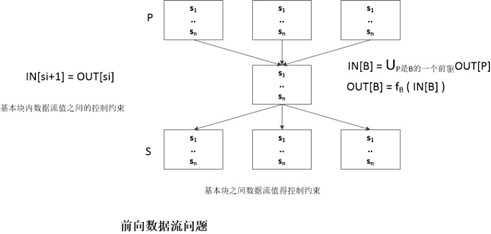
图中展示出来的是基本块之间的前向数据流问题的约束方程。后向束流问题的方程如下图所示。

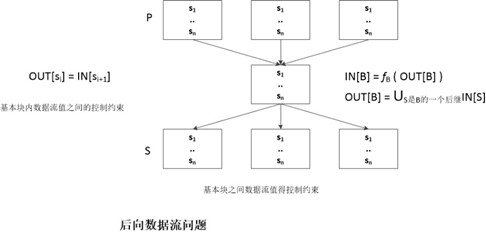
数据流分析就是根据这一组约束，得到一个满足这些约束的解。和线性算法方程不同，数据流方程通常没有唯一解。数据流分析的目标是寻找一个最"精确的"满足这两组约束（即控制流和传递函数）的解，当然这个解必须是保守的，能够保证我们根据这个解进行代码优化不会导致不安全的转换。

当然数据流分析，不是直接联立方程求解，一般是通过一种迭代分析的方法求解的。

到达定值

什么是到达值

"到达值"是最常见的和有用的数据流模式之一。编译器能够根据到达定值信息知道x在点p上的值是否为常量，而如果x在点p上被使用，则调试器可以指出x是否未经定值就被使用。

如果存在一条从紧随在定值d后面的程序点到达某一个程序点p的路径，并且在这条路径行d没有被"杀死"，我们就说定值d到达程序点p。如果在这条路径上有对变量x的其他定值，我们就说变量x的这个定值（定值d）被"杀死"了。

到达值的示意图如下所示。

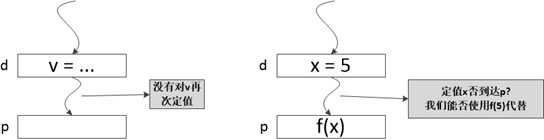
注：上面这个图不严谨，p是程序点，应该紧挨着下面的矩形而不是表示矩形。图中的矩形表示的是一条语句。

到达值有以下用法：

创建use/def链

常量传播

循环不变量外提

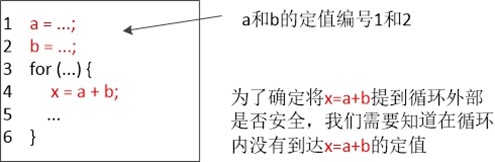
变量x的一个定值是（可能）将一个赋值给x的语句。过程参数，数组访问和间接引用都可以有别名，因此指出一个语句是否向特定程序变量x赋值并不是件很容易地事情。

存在别名的情况下需要作别名分析，如果为了提高分析效率而不介意损失一些分析精度的话，可以做保守估计，例如我们不知道当前语句对哪个变量赋值，我们就在此处针对每个变量产生一个定值。这是一种无奈的折中。此处我们不考虑别名情况。

到达定值的传递函数

首先我们做一些假设：

一个语句节点至多能够对一个变量定值

我们可以通过节点编号索引到该赋值语句

当然，在实际情况中一个语句节点可能会对不止一个变量定值。下面我们定义一下gen[n]函数和kill[n]函数。

gen[n]:节点n产生的定值（假设一个语句节点至多一个定值）

kill[n]:节点n"杀死"的定值

程序语句	gen[s]	kill[s]
s: t = b op c	{s}	def[t] - {s}
s: t = M[b]	{s}	def[t] - {s}
s: M[a] = b	{s}	{*} - {s}
s: if a op b goto L	{}	{}
s:goto L	{}	{}
s: L:	{}	{}
s: f(a, …)	{}	{}
s: t = f(a, …)	{s}	def[t] - {s}

 

上面的表格列举了一些程序语句的gen和kill传递函数形式。第一行的列举的"s:t=b op c",产生了定值s并"杀死"了除定值s以外所有对变量t的定值。

注意：定值是一个程序，对同一个变量可以存在多个不同的定值

我们也可以先计算出各个程序语句的gen和kill结果，然后综合基本块中的各个语句生成整个基本块的gen和kill集合。如下图所示，其中我们先默认各个基本块的起始和结束处所有定值都可以到达，下图程序中总共有7个定值，分别为d1,d2,d3,d4,d5,d6,d7.

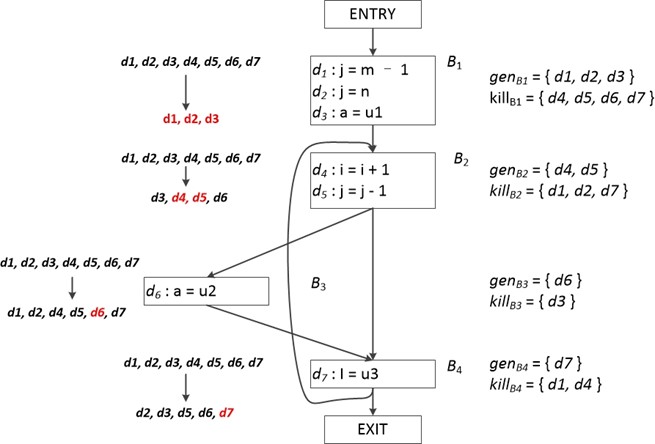
经过第一次的传递函数作用，各个基本块到达定值集合的变化情况如图左所示。

到达值的保守性

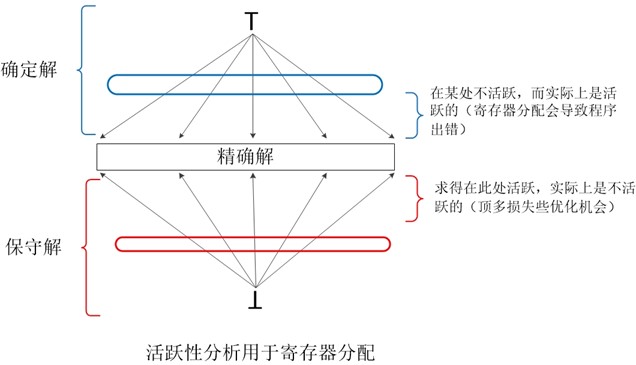
在前面介绍数据流分析时，曾经提到过数据流分析允许一定的不精确性。但是它们都是在"安全"或者说"保守"的方向上不精确。如下图所示：

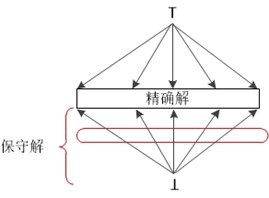
只要我们得到的解偏于保守的一方即可，然后再尽力的向精确的方向靠近，不同的应用"保守"的定义也不同。在大部分到达定值的应用中，在一个定值不可能到达某点的情况下假设其能够到达是保守的。如下图所示：

因此在设计一个数据流模型的时候，我们必须知道这些信息将如何被使用，并保证我们做出的任何估算都是在"保守"或者说"安全"的方向上。每个模式合区应用都要单独考虑。

也就是说，不能套用同一个模式来判断"保守"或者"安全"的方向，在可用表达式中，"安全"的定义就和到达定值不同。如果可用表达式没有到达某个程序点，而得出的解表明到达了，则这是不安全的。

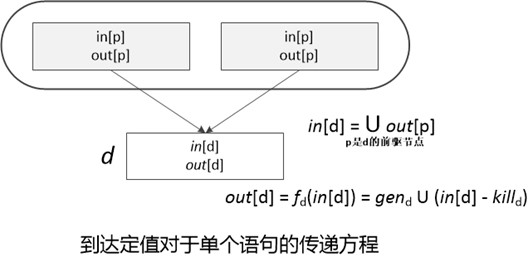
到达定值的传递方程以及控制流方程

到达定值对于单个语句的传递方程如下图所示，一个基本块内的依据就是按照这组方程建立起联系的。和单个语句一样，一个基本块也会生成一个定值集合，并杀死一个定值集合。

根据基本块之间的控制流得到的约束集合，我们可以生成一个控制流方程。其实控制流方程的含义就是在路劲交叉点进行数据流值的交汇，在到达定值中，交汇运算就是并集运算（）。

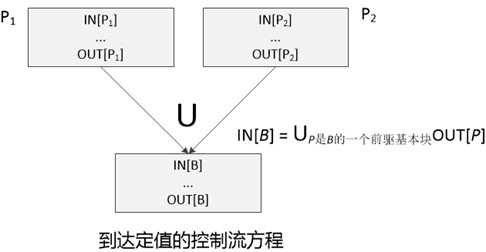
对于到达定值来说，只要一个定值能够沿着至少一个路径到达某个程序点，就说这个定值到达该程序点。所以控制流方程的交汇运算时并集，但是对于其他一些数据流问题交汇运算时交集，例如可用表达式。

到达定值的迭代分析算法

假设每个控制流图都有两个空的基本块，代表了控制流图的ENTRY节点和EXIT节点。由于没有定值到达这个图的开始，所以基本块ENTRY的传递函数是一个简单的返回空集的常函数，即OUT[ENTRY]=空集。

到达定值问题使用下面方程的定义：

OUT[ENTRY]=空集

且对于所有的不等于ENTRY的基本块B，有

OUT[B]=gen(B)(IN[B]-kill(B))

IN[B]= OUT[P],其中P是B的一个前驱基本块

我们可以使用下面的算法来求这个方程组的解。

到达定值算法：

输入：一个流图，其中每个基本块B的kill(B)集合gen(B)集都已经计算出来了。

输出：到达流图中各个基本块B的入口点和出口点的定值的集合，即IN[B]和OUT[B]。

方法：我们使用迭代的方法来求解。一开始，我们"估计"对于所有基本块B都有OUT[B]=空集，并逐步逼近想要的IN和OUT值。因为我们必须不停地迭代直到各个IN值（因此各个OUT值也）收敛，所以我们使用一个bool变量change来记录每次扫描各基本块时是否有OUT值发生变化。

从算法中我们可以明确看到，数据流值是从前驱P到IN[B]然后在流向OUT[B]这样一个从前向后不断传播的。然后从空集不断扩大直到越过精确解到达"保守解"。

迭代算法不断从空向到达定值结果越来越多的方向靠近，最终会跨越精确解到达保守解的部分，主要因为两个原因导致一定会越过精确解：

不考虑路径条件，假设所有路径都可达；这样某些定值最终会到达他们本来到达不了的地方

存在别名时，给无法确认的"别名"赋值时，给所有变量添加一个定值（注意此处并没有kill掉所有的定值，因为添加所有可能的定值，删除肯定被kill掉定值，这样才能保证"保守"）

这个算法还有可以改进的地方，其中一个就是精心安排迭代分析时基本块的顺序，基本按照CFG从入口ENTRY到EXIT顺序。如果当前基本块的到达定值结果发生了改变，那么就把其所有后继基本块加入待迭代的工作列表workList。

另外到达定值使用了一种位向量的结构，来表示到达定值集合。即每个程序点的到达定值使用一个为向量表示，例如该程序有7个定值，那么位向量为7，初始向量"0000000"表示此时定值为空，如果第3号定值到达了当前程序点，那么位向量为"0010000"

活跃变量的数据流方程

我们给出两个定义：

• def(or definition)
• use

def[v] = 定义变量v的所有CFG节点集合
def[n] = 节点n定义的变量集合

use[v] = 使用变量v的CFG节点集合
use[n] = 在节点n使用的变量集合

计算活跃性的规则：

（1）产生活跃性

（2）活跃性如何越过程序语句节点之间的边

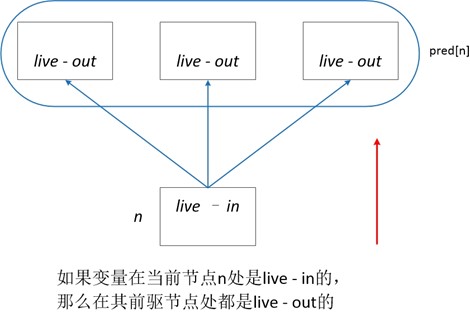
（3）活跃性如何越过程序语句节点

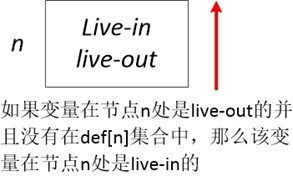
我们列出活跃变量的数据流方程如下所示，注意此处我们将语义约束和控制约束同时写出来了（因为我们现在是以单个程序语句为图节点，而不是单个基本块）

• in [n] = use [n] U ( out [n] - def [n] )
• out [n] = U in [s] , 其中s是节点n的后继节点

从这两个方程我们可以看出，对于活跃变量分析来说数据流是从后向前传播的。我们这里解释一下为什么要从out[n]中删除def[n]，

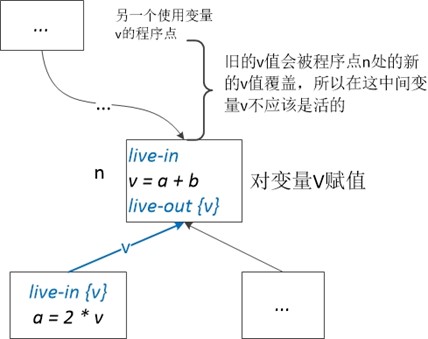
下面给出活跃变量分析的算法：

注：此处CFG是以程序语句为单个节点构建的

当然这个算法没有考虑到CFG图中节点的顺序，效率比较低，我们将CFG图中的节点反序，用来求解。改进算法如下：

我们也可以基本块为单位来就行活跃变量的分析，但是我们得首先根据基本块中程序语句的传递函数合并成为基本块的传递函数。定义如下：

• def [B] 是指如下变量的集合，这个变量在B中的定值（即被明确地）先于任何对它们的使用
• use [B]是指如下变量的集合，它们的值可能在B中先于任何对它们的定值被使用

注意：上述我们标注的黑色部分，在def[B]中需要被明确定值，而在use中条件弱化，只需要可能就行了。类似于到达定值，这样做是为了保守性。在活跃变量中，假设变量活跃到程序结束是没有问题的，只是会损失些可以优化的点（例如寄存器分配时两个变量的活跃区间相互重叠的概率就会变得很大），但是如果将变量的活跃期缩短的话，有可能就将该寄存器挪做他用，这样就会导致程序错误。所以在活跃变量分析中，将活跃变量尽可能的向前传播是有利于偏向保守的。但是不能一味的偏于保守，否则得到的信息就没有任何价值，在保证保守的同时，尽可能的向精确解靠拢（所以杀死被明确赋值的变量）

所以我们在杀死变量时（即在基本块内明确定义，在 def[B] 中）必须明确规定，但是尽可能地向前传播（也就是如果可能在use[B] 中，直接加入就好）。如下图所示，我们所求得的结果必须能够保证在保守解部分，并尽力向精确解靠近。为了保证保守性，需要做到如下两点：

• 忽略路径分支条件，保证所有路径都可达
• 只要有可能是活的，就向其中加入该变量。只有在该活跃变量被明确杀死时（例如被明确赋值），才删除

如果以基本块为单位，那么得到的数据流方程如下图所示：

第一个方程描述了边界条件，即在程序出口处没有变量是活跃的。
第二个方程说明一个变量要在进入一个基本块时活跃，必须满足两个条件中的一个：要么它在基本块内被重新定值之前就被使用；要么它在基本块的出口处活跃且在基本块内没有对它进行重新定值。
第三个方程说明一个变量在一个基本块的出口处活跃当前仅当它在该基本块的某个后继入口处活跃。

和到达定值相同，活跃变量不需要在后继基本块入口都活跃，只要在其中一个基本块入口活跃即可。但是活跃变量是后向数据流模式。在各个数据流模式中，我们都沿着路径传播信息，有的数据流问题，要求对应性质需要在所有路径上都成立，而有的数据流只需要存在一个满足该性质的路径即可。

基于基本块的活跃变量分析算法：
输入：一个流图，其中每个基本块的use和def已经计算出来了。
输出：该流图中的各个基本块B的入口和出口处的活跃变量集合，即 IN[ B ] 和 OUT[ B ]。

该算法得到的具有最小活跃变量（亦即尽量向精确解靠近）的集合。

可用表达式

如果从流图入口结点到达程序点 p 的每条路径都对表达式 x + y 求值，且从最后一个这样的求值之后到p点的路径上没有再次对x或y赋值，那么 x + y 在 p 点上可用(available)。

注意在可用表达式的定义中，我特意加黑了每条路径，这是和到达定值不同的，对于到达定值来说至少存在一条这样的路径即可。

对于可用表达式数据流模式而言，如果一个基本块对 x 或 y 赋值（或可能对它们赋值），并且之后没有再重新计算 x + y，我们就说该基本块"杀死"了表达式 x + y。

如果一个基本块一定对 x + y 求值，并且之后没有再对 x 或 y 定值，那么这个基本块生成表达式 x + y 。

可用表达式信息的主要用途就是寻找全局公共子表达式。每个程序都有有限个表达式，这有限个表达式就是可用表达式数据流分析的值域，也就是每个程序点的可用表达式就是这个值域的子集。

int z = x * y;

print s + t;

int w = u / v;

// ...

// program contains expressions { x * y, s + t, u / v, ...}

• 1
  

• 2
  

• 3
  

• 4
  

• 5
  

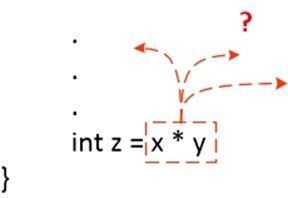
可用性是表达式在数据流中的一个属性，"这个表达式是否计算过？"。在一条指令之前，每个表达式只能是可用或者不可用，所以通常都是从指令的角度来考虑表达式的可用性，每条指令（或者流图中的一个结点）都关联着一组可用表达式。

int z = x * y;

print s + t;

int w = u / v; // 3: avail(3) = { x * y, s + t}

• 1
  

• 2
  

• 3
  

例如在结点3处，有两条可用表达式"x * y" 和 "s + t"。从很多方面来看，可用表达式和活变量都有相似之处，都是数据流的一种属性，并且在每个程序点都关联着一组值的集合。在活跃变量分析中，数据流从后向前传播，一个对 x 的赋值语句，会"杀死"变量x的活跃性，在可用表达式的分析中，数据流从前向后传播，一个对 x 的赋值语句会"杀死"所有包含 x 运算子的表达式。

除了数据流方向这一个区别之外，还有一个很重要的区别，就是在可用表达式分析中，我们必须能够保证该表达式在当前程序点绝对可用，也就是说我们必须保证该表达式被计算过（即使有丢失可用表达式的可能），而不是该表达式在此处可能可用。也就是说可用表达式分析是一种must分析，而活跃变量分析是一种may分析。

如果一个表达式被认为是可用的，我们有可能会做一些比较危险的事情（例如删除重复计算该表达式的指令）。在活变量分析中，更多的活变量就更能够保证安全性，但是在可用表达式中，越少的可用表达式才更能保证安全性。

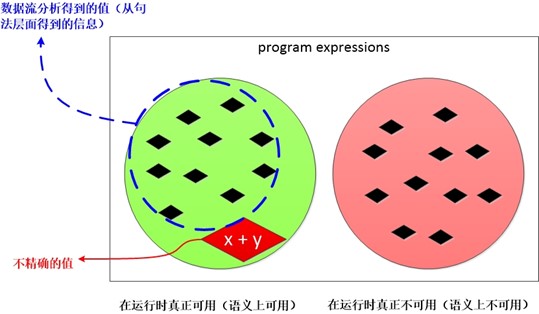
当程序运行时可用表达式和不可用表达式如下图所示，这个图表示的动态执行时的精确解（也就是如果某个基本块不可能执行到，那么这个基本块对可用表达式分析的影响为0）。

假设有以下代码，在数据流分析中不可能真正确切的知道哪些路径可达，所以假设所有路径可达是安全的，虽然会损失些可以优化的机会。

在安全的前提下，数据流分析还是会尽量向精确靠近，这样才能把优化发挥的更彻底。上述代码对应的可用表达式的图示如下。其中 x + y 是我们在数据流分析的过程中将其杀死的，其实在真正代码的执行过程中，B3块可能不会被真正执行，也就是说 x + y 可能是可用的。但是数据流分析的第一准则是安全性，然后才会在安全的前提下做更为激进的分析。和活变量分析类似，我们尽量会在安全的前提下，向精确解靠近。

我们可以用类似于计算到达定值的方式计算可用表达式。假设 U 是所有出现在程序中一个或多个语句的右部的表达式的全集。对于每个基本块B，令IN[ B ]表示在B的开始处可用的的U中的表达式的集合。令OUT[ B ]表示在B的结尾处可用的表达式集合。定义e_gen[B]为B生成的表达式的集合，而e_kill[B]为被B杀死的U中的表达式的集合。所以我们可以相关的数据流方程和控制流方程。

上面的方程和到达定值的方程组看起来几乎一样，但是一点很重要的区别是这个方程组的交汇运算是交集运算，而不是并集运算。因为只有当一个表达式在一个基本块的多有前驱的结尾处都可用，它才会在该基本块的开头可用。

在到达定值方程的过程中，我们首先假设任何地方都没有定值到达，然后逐渐增大到到达定值的集合，最终构建得到该解。我们最终会求解到达定值方程组，得到符号"到达"定义的最小集合。

而在求解可用表达式的过程中，我们首先假设除了入口块之外的所有基本块的出口处，所有可用表达式都是可用的，然后不断的将这个解缩小，直到得到一个最大的可用表达式集合的解。

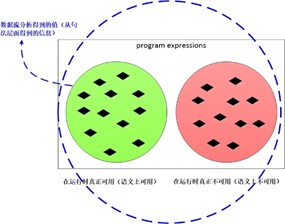
例如我们开始假设所有表达式可用，然后不断的缩减得到的解，直到越过了精确解范畴。

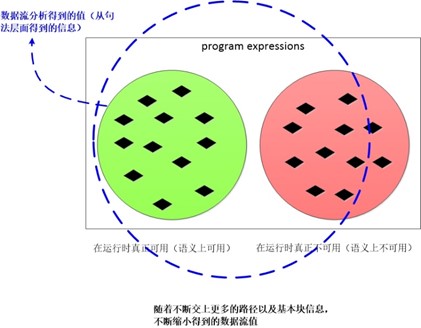
由于数据流分析会忽略所有的路径条件，假设所有的路径可达，所以数据流解的集合会不断的缩小直到一个最大的精确的安全解。

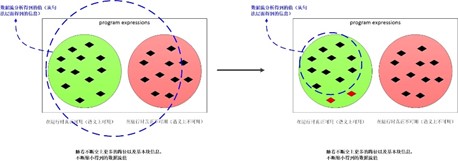
这里我们证明一下为什么考虑全路径的情况下，一定会越过精确解。考虑下面的代码：

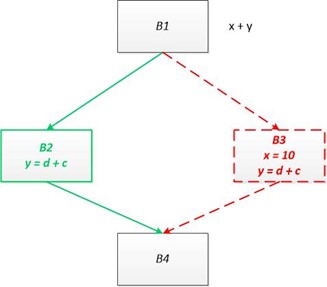
（1）多考虑一个路径，肯定会杀死一个原有的可用的表达式
（2）即使多考虑的路径中会生成新的可用表达式，但是由于数据流方程是交集运算，所以单单多考虑的路径的生成还不行，还需要其他的路径都生成该表达式，该表达式才会生成出来。也就是说，多考虑的路径中生成的表达式其实没有任何意义。

例如上图中的代码，假设 B1 -> B3 -> B4 这条路径不可达，B3块会杀死表达式x + y，虽然会生成表达式 d + c 但是由于可用表达式的交汇运算时交集，所以必须B2块生成表达式 d + c 才算真正生成表达式 d + c ，也就是无效路径生成的表达式其实没有意思的。也就是多考虑一条路径只会杀死更多的表达式。

不知道一个表达式是可用的只会使我们失去改进代码的机会，而把一个不可用的表达式则会使我们改变程序的计算结果。可用表达式的迭代算法如下所示：

下面我们总结一下前面所提到过的MUST和MAY分析。

特点	May	Must
safe	更大的集合	更小的集合
desired information	small set	large set
Gen	添加可能为真的值	只添加保证为真的值
Kill	只删除保证为假的值	删除所有可能为假的值
merge	union	intersection

通过上面的表格，我们可以看出May分析是尽可能向集合增大的方向前进，而Must分析是尽可能的向集合减小的方向前进。那么有没有一个统一的数据流分析框架来表示呢，不用去关注最终得到的解释最大不动点还是最小不动点，是用交集还是用并集等等。答案是有，后面我们介绍数据流分析中格的概念，格这种数据结构是一个非常直观的表示数据流分析的框架。

Sound And Complete

前面我通过可用表达式的例子说明精确解与保守解的概念，其实这种提法并不标准。下面我摘抄《A Brief Introduction to Static Analysis - Sam Blackshear》讲义中的内容。

当我们编写一个程序的时候，我们希望知道程序是否满足某个属性，例如程序P是否没有空指针解引用（NPD），或者程序中的所有的类型转换是否是安全的。如果对程序P进行手工验证，在程序P比较复杂的时候，过程会很繁琐。所以可以通过一个程序（或者静态分析工具）去验证程序P的某些属性是否满足。

但是验证某个程序的属性是不可判定的，见如何理解莱斯定理对程序静态分析的限制。

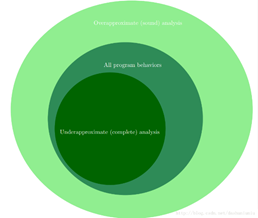
虽然我们无法得到程序的精确解，但是我们可以使用overapproximation或者underapproximation来尝试得到一个较为精确的解。

• A sound static analysis overapproximates the behaviors of the program. A sound static analyzer is guaranteed to identify all violations of our property φ, but may also report some "false alarms", or violations of φ that cannot actully occur.
• A complete static analysis underapproximates the behaviors of the program. Any violation of our property φ reported by a complete static analyzer corresponds to an actual violation of φ, but there is no guarantee that all actual violations of φ will be reported.

上面的的sound static analysis其实就对应我们上面说的保守解，是一种overapproximation，就是考虑程序中实际并不可行的路径，所以能够覆盖完所有的违反属性φ的场景，但是有误报。

而上面的complete static analysis是一种就对应上面我们所描述的超过精确解的值，这些值保证都违反了φ，但是并不能覆盖完所有的值，有漏报。

Note that when a sound static analyzer reports no errors, our program is guaranteed not to violate φ! This is a powerful guarantee. As a result, most static analysis tools choose to be sound rather than complete.

但是在某些静态分析工具中在某些场景中是不可能做到sound的，例如clang static analyzer，在指针场景中，指针ptr有可能指向任意的变量，如果要对指针ptr指向的内存区域进行赋值，"sound static analysis"会将程序中所有变量进行赋值，那么继续向下就会变得非常不精确，这是不可能接受的，整个分析过程会得不到任何有价值的信息。