OpenGL基础

20' 抛物面，法向量

10' 抛物面

#define DELTA 0.1

#define PI2 2*3.14159

double parabolicSurf[36][10][3];

void MakeParabolicSurface()

{

    for (int a = 0; a < 36; a++)

    {

        for (int r = 0; r < 10; r++)

        {

            parabolicSurf[a][r][0] = (DELTA*r)*cos(a*PI2 / 36.0);

            parabolicSurf[a][r][1] = (DELTA*r)*sin(a*PI2 / 36.0);

            parabolicSurf[a][r][2] = (DELTA*r)*(DELTA*r);

        }

    }

}

 

10' 法向量

void Normal(double a[3], double b[3], double c[3], double n[3])

{

    int i;

    double p[3], q[3];

 

    for (i = 0; i < 3; i++)

    {

        p[i] = b[i] - a[i];

        q[i] = c[i] - a[i];

    }

 

    n[0] = p[1] * q[2] - p[2] * q[1];

    n[1] = p[2] * q[0] - p[0] * q[2];

    n[2] = p[0] * q[1] - p[1] * q[0];

 

    double t = n[0] * n[0] + n[1] * n[1] + n[2] * n[2];

 

    t = sqrt(t);

 

    for (i = 0; i < 3; i++)

        n[i] /= t;

}

20'切平面方程，曲率

切平面方程：高等数学(下)p123—p128

曲率：高等数学(上)p208-p211

20'几何变换，齐次坐标

 

 

例题：

20'名词解释

参数样条曲线

样条是一根富有弹性的细木条或类似物，其两端连接着起固定作用的压铁。通过调整样条两端的压铁可以改变样条的形态，它是手工绘制自由曲线的一种工具。沿着样条绘制的曲线称为样条曲线。

贝塞尔曲线的凸包性

贝塞尔基函数

自由曲线

形状比较复杂、不能用二次方程来表示的曲线（曲面）称为自由曲线（曲面），也称为复杂曲线(曲面)，通常以三次参数方程来表示。

曲线拟合

给定一个点列，用该点列来构造曲线的方法称为曲线拟合。

曲线插值

已知曲线上的一个点列，求曲线上的其他点的方法称为曲线插值。

参数多项式曲线

样条曲线可以表示为参数多项式曲线或分段参数多项式曲线。

齐次坐标表示法

所谓齐次坐标表示法就是用n＋１维向量表示一个n维向量，即n维空间中的点的位置向量(P1，P2，…Pn)被表示为具有n＋１个坐标分量的向量(hP1,hP2,…，hPn，h)。

规范化过程

从平面上点的齐次坐标，经齐次坐标变换，最后转换为平面上点的坐标，这一变换过程称为规范化过程。

直线反走样

通常，我们把由离散量表示连续量引起的失真称为走样；把减少或克服走样效果的技术称为反走样技术，简称反走样。

直线如何反走样

把像素作为一个有限区域，对区域采样来调整像素的亮度，以光顺边界来减小锯齿现象

20' Hermite样条曲线

例题：已知平面上三点P1(0,0)，P2(1,1)和P2(2,0)，用自由端约束条件计算三次Hermite样条曲线Q(t)使得它拟合点列{P1，P2，P3}，并将Q(t)表示为参数序列{0，1，2}上的分段参数多项式函数。

解：由Hermite样条曲线二阶导数的连续性及自由端约束条件得到

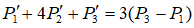
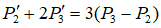
解方程组得到

由控制点的坐标得到

由Hermite曲线方程

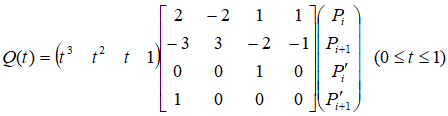
得到

 

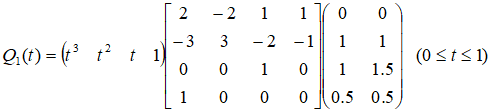
所求曲线方程为：