Description

Lele now is thinking about a simple function f(x).

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.
 

Input

The problem contains mutiple test cases.Please process to the end of file.
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9.
 

Output

For each case, output f(k) % m in one line.
 

Sample Input

10 9999
1 1 1 1 1 1 1 1 1 1
20 500
1 0 1 0 1 0 1 0 1 0
 

Sample Output

45
104
 
   盗用一下图。。。。
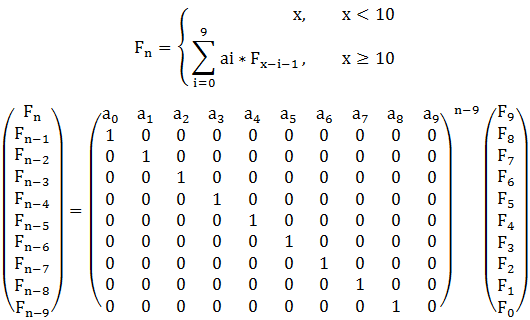
   也怪我学艺不精，理解力也比较差，第一次做这类题目就花了这么长时间，不过幸好本人脾气好，坚持下去了，其诸多“辛酸”的经验，特地和大家分享。。。
    那就直接上代码啦。。。
 
 
#include <stdio.h>
#include <string.h>
using namespace std;
int i,j,m;
long long k;
 
//.......这是矩阵相乘
void MatrixMul(int x[][10],int y[][10])
{
    long long tmp[10][10];
    memset(tmp,0,sizeof(tmp));
    for (i=0;i<10;i++)
        for (j=0;j<10;j++)
            for (k=0;k<10;k++)
                tmp[i][j]=(tmp[i][j]+x[i][k]*y[k][j])%m;  //.......如果因为偷懒而写成tmp[i][j]+=x[i][k]*y[k][j]%m ，那就错了哦
    for (i=0;i<10;i++)
        for (j=0;j<10;j++)
            x[i][j]=tmp[i][j]%m; //.......再取一次余，减少运算时间
}
 
//.......这是快速幂求模了
int FastPow(int a[][10],int b)
{
    int res[10][10];
    long long f;
      for (i=0;i<10;i++)
        for (j=0;j<10;j++)
            {
                if (i==j)
                   res[i][j]=1;
                else
                   res[i][j]=0;
            }
            while (b)
            {
                if (b & 1) //.......这样写能把b转化成二进制哦，然后判断转化而来的二进制数的末位是否为1而进行快速幂的计算
                   MatrixMul(res,a);
                MatrixMul(a,a);
                b=b>>1; //.......记得左移哦，貌似有点抽象呢
            }
            f=0;
            for (i=0;i<10;i++)
                f=(f+(9-i)*res[0][i])%m;
    return f;
}
 

int main ()
{
    int ans;
    int map[10][10];
    while (~scanf ("%lld%d",&k,&m))
    {
        for (i=0;i<10;i++)
            scanf ("%d",&map[0][i]);
        for (i=1;i<10;i++)
            for (j=0;j<10;j++)
            {
                   if (i==(j+1))
                      map[i][j]=1;
                   else
                      map[i][j]=0;
            }
        if (k<10)
       {
           printf ("%d\n",k%m);
           continue;
       }
       ans=FastPow(map,k-9);
       printf ("%d\n",ans);
    }
    return 0;
}
(。。。。。。。没必要为了防止溢出而把所有的量都定义为long long)
（呃。。。关于取余什么的看不太懂的，可以详查快速幂的原理）