ZJOI2015-2016 做题笔记
ZJOI2015-2016 做题笔记
题目:https://www.luogu.com.cn/problem/list?tag=32,33%7C88&page=1
[ZJOI2015] 幻想乡战略游戏
首先考虑最优选点是在哪里,不难发现是这棵树的点权重心,且与边权无关。
而求重心的一个方法就是满足 中最深的点。
假设现在确定了重心 ,然后需要求 ,直接拆公式:
前面两个式子直接算,对于后面的式子是经典问题,每次对 的链经行覆盖,然后每次查询 的链。
上述的东西可以树剖做。同时对于找重心,不难发现满足 是一根从上到下的链,dfn 序递增,所以直接在线段树上二分即可。
时间复杂度 。
ケロシの代码
const int N = 1e5 + 5;
int n, m;
int fi[N], ne[N << 1], to[N << 1], ew[N << 1], ecnt;
int d[N], sz[N], fa[N], son[N];
int dfn[N], rnk[N], top[N], cnt;
void add(int u, int v, int w) {
ne[++ ecnt] = fi[u];
to[ecnt] = v;
ew[ecnt] = w;
fi[u] = ecnt;
}
void dfs1(int u) {
sz[u] = 1;
son[u] = - 1;
for(int i = fi[u]; i; i = ne[i]) {
int v = to[i], w = ew[i];
if(v == fa[u]) continue;
fa[v] = u;
d[v] = d[u] + w;
dfs1(v);
sz[u] += sz[v];
if(son[u] == - 1 || sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int tp) {
dfn[u] = ++ cnt;
rnk[cnt] = u;
top[u] = tp;
if(son[u] != - 1) dfs2(son[u], tp);
for(int i = fi[u]; i; i = ne[i]) {
int v = to[i];
if(v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
struct SgT {
int le[N << 2], ri[N << 2], len[N << 2];
ll F[N << 2]; int S[N << 2], T[N << 2];
void pushup(int u) {
F[u] = F[u << 1] + F[u << 1 | 1];
S[u] = max(S[u << 1], S[u << 1 | 1]);
}
void push(int u, int x) {
T[u] += x;
S[u] += x;
F[u] += 1ll * x * len[u];
}
void pushdown(int u) {
if(T[u]) {
push(u << 1, T[u]);
push(u << 1 | 1, T[u]);
T[u] = 0;
}
}
void build(int u, int l, int r) {
le[u] = l, ri[u] = r;
if(l == r) {
len[u] = d[rnk[l]] - d[fa[rnk[l]]];
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
len[u] = len[u << 1] + len[u << 1 | 1];
}
void modify(int u, int l, int r, int x) {
if(l <= le[u] && ri[u] <= r) {
push(u, x);
return;
}
pushdown(u);
int mid = le[u] + ri[u] >> 1;
if(l <= mid) modify(u << 1, l, r, x);
if(mid < r) modify(u << 1 | 1, l, r, x);
pushup(u);
}
ll query(int u, int l, int r) {
if(l <= le[u] && ri[u] <= r) {
return F[u];
}
pushdown(u);
int mid = le[u] + ri[u] >> 1;
if(r <= mid) return query(u << 1, l, r);
if(mid < l) return query(u << 1 | 1, l, r);
return query(u << 1, l, r) + query(u << 1 | 1, l, r);
}
int get(int u) {
if(S[u] * 2 < S[1]) return - 1;
if(le[u] == ri[u]) return rnk[le[u]];
pushdown(u);
int val = get(u << 1 | 1);
if(val == - 1) val = get(u << 1);
return val;
}
} t;
void modify(int u, int x) {
while(u) {
t.modify(1, dfn[top[u]], dfn[u], x);
u = fa[top[u]];
}
}
ll query(int u) {
ll res = 0;
while(u) {
res += t.query(1, dfn[top[u]], dfn[u]);
u = fa[top[u]];
}
return res;
}
void solve() {
cin >> n >> m;
REP(_, n - 1) {
int u, v, w;
cin >> u >> v >> w;
add(u, v, w);
add(v, u, w);
}
dfs1(1); dfs2(1, 1);
t.build(1, 1, n);
ll sum = 0, res = 0;
REP(_, m) {
int u, x;
cin >> u >> x;
modify(u, x);
sum += x;
res += 1ll * x * d[u];
int mid = t.get(1);
cout << res + 1ll * sum * d[mid] - query(mid) * 2 << endl;
}
}
[ZJOI2015] 诸神眷顾的幻想乡
对于多个串中的本质不同字符串个数,想到广义 SAM,但是有些链会在树上拐弯,难以统计。
不难发现题目保证叶子很少,而对于每一个叶子都作为根搜一边,所有的链都会被搜到。
这样就合并出了一个比较巨大的字典树,在这个上面跑广义 SAM 即可。
设叶子数为 ,则时间复杂度为 。
ケロシの代码
const int N = 1e5 + 5;
const int M = 2e6 + 5;
int n, m, a[N], ru[N];
int fi[N], ne[N << 1], to[N << 1], ecnt;
int tr[M][10]; int pre[M], p[M], idx;
struct Node {
int len, link;
int nxt[10];
} st[M << 1]; int sz;
void add(int u, int v) {
ne[++ ecnt] = fi[u];
to[ecnt] = v;
fi[u] = ecnt;
}
void dfs(int u, int fa, int pos) {
if(! tr[pos][a[u]]) {
tr[pos][a[u]] = ++ idx;
pre[idx] = pos;
}
pos = tr[pos][a[u]];
for(int i = fi[u]; i; i = ne[i]) {
int v = to[i];
if(v == fa) continue;
dfs(v, u, pos);
}
}
int insert(int x, int lst) {
int cur = ++ sz;
st[cur].len = st[lst].len + 1;
int p = lst;
while(p != - 1 && ! st[p].nxt[x]) {
st[p].nxt[x] = cur;
p = st[p].link;
}
if(p == - 1) {
st[cur].link = 1;
}
else {
int q = st[p].nxt[x];
if(st[p].len + 1 == st[q].len) {
st[cur].link = q;
}
else {
int cln = ++ sz;
st[cln].len = st[p].len + 1;
st[cln].link = st[q].link;
REP(i, 10) st[cln].nxt[i] = st[q].nxt[i];
while(p != - 1 && st[p].nxt[x] == q) {
st[p].nxt[x] = cln;
p = st[p].link;
}
st[cur].link = st[q].link = cln;
}
}
return cur;
}
void build() {
st[1].link = - 1;
sz = 1;
p[0] = 1;
queue<PII> q;
REP(i, m) if(tr[0][i]) q.push({tr[0][i], i});
while(! q.empty()) {
auto h = q.front();
q.pop();
int u, c; tie(u, c) = h;
p[u] = insert(c, p[pre[u]]);
REP(i, m) if(tr[u][i]) q.push({tr[u][i], i});
}
}
void solve() {
cin >> n >> m;
FOR(i, 1, n) cin >> a[i];
REP(_, n - 1) {
int u, v;
cin >> u >> v;
add(u, v);
add(v, u);
ru[u] ++; ru[v] ++;
}
FOR(i, 1, n) if(ru[i] == 1) dfs(i, 0, 0);
build();
ll ans = 0;
FOR(i, 2, sz) ans += st[i].len - st[st[i].link].len;
cout << ans << endl;
}
[ZJOI2015] 幻想乡 Wi-Fi 搭建计划
先对所有的点排序,然后不难发现结论,就是对于单独的一边,路由器点都是贡献了一段区间的 WiFi 点。
有了这个结论,就不难发现可以 dp,设 表示枚举到第 个 WiFi 点,上边最后一个匹配点是点 ,下边最后一个匹配点是点 ,让然后进行转移,每次是用 或 就不用额外代价,新开点就需要算新代价,像这样进行 DP 即可。
时间复杂度 。
ケロシの代码
const int N = 1e2 + 5;
const int INF = 1e9 + 7;
int n, m, R;
struct Point {
int x, y, w;
bool operator < (const Point & A) const {
return x < A.x;
}
} a[N], p[N], b1[N], b2[N];
int cnt, t1, t2;
int dp[N][N][N];
ll sq(ll x) {
return x * x;
}
bool C(Point A, Point B) {
return sq(A.x - B.x) + sq(A.y - B.y) <= sq(R);
}
void solve() {
cin >> n >> m >> R;
FOR(i, 1, n) cin >> a[i].x >> a[i].y;
REP(_, m) {
int x, y, w;
cin >> x >> y >> w;
if(y < 0) b1[++ t1] = {x, y, w};
else b2[++ t2] = {x, y, w};
}
FOR(i, 1, n) {
bool ok = 0;
FOR(j, 1, t1) if(C(a[i], b1[j])) ok = 1;
FOR(j, 1, t2) if(C(a[i], b2[j])) ok = 1;
if(ok) p[++ cnt] = a[i];
}
sort(p + 1, p + cnt + 1);
sort(b1 + 1, b1 + t1 + 1);
sort(b2 + 1, b2 + t2 + 1);
b1[0] = b2[0] = {INF, INF, 0};
memset(dp, 0x3f, sizeof dp);
dp[0][0][0] = 0;
FOR(i, 1, cnt) FOR(l, 0, t1) FOR(r, 0, t2) {
FOR(k, 1, t1) if(C(p[i], b1[k]))
chmin(dp[i][k][r], dp[i - 1][l][r] + (k != l ? b1[k].w : 0));
FOR(k, 1, t2) if(C(p[i], b2[k]))
chmin(dp[i][l][k], dp[i - 1][l][r] + (k != r ? b2[k].w : 0));
}
int ans = INF;
FOR(i, 0, t1) FOR(j, 0, t2) chmin(ans, dp[cnt][i][j]);
cout << cnt << endl;
cout << ans << endl;
}
[ZJOI2015] 地震后的幻想乡
首先证一下 个在 之间的随机数中第 小的期望,考虑一个圆,上面随机撒 个点,相邻点的距离期望为 ,然后从一个点处把这个圆剪断,剩下的就是随机的 个点,第 小的明显期望就是 。
接下来题意就是求最小生成树最大边的期望,设最大边为第 小的概率为 ,那么 ,然后推式子:
然后考虑这个 ,也就是最小生成树最大边大于第 小的边的概率是个什么,不难发现这就就等价于最大边小于第 小的边,也就是只用前 小的边,且无法构建生成树的概率。
这个就好做了,只用前 小的边无法构建生成树的概率,就等于随机选 条边无法构建生成树的概率,就等于选 条边无法构建生成树的方案数除掉 。
接下来只要求方案数就可以了,不难想到状压 dp,设 为点集 的诱导子图的边数, 为点集 中选了 条边并不连通的方案数, 为连通的方案数,显然有 。
考虑转移,但是很容易算重。考虑一种方法,就是随便找一个 中的点 ,枚举 所在的连通块 ,然后 之外的部分随便连,不难发现这样转移不重不漏,转移方程:
时间复杂度 。
ケロシの代码
const int N = 10;
const int M = 50;
int n, m;
ll C[M][M], s[1 << N], f[1 << N][M], g[1 << N][M];
int lowbit(int x) {
return - x & x;
}
void solve() {
cin >> n >> m;
FOR(i, 0, m) {
C[i][0] = 1;
FOR(j, 1, i) C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
REP(_, m) {
int u, v;
cin >> u >> v;
u --; v --;
REP(S, 1 << n) if(S >> u & 1) if(S >> v & 1) s[S] ++;
}
REP(i, n) g[1 << i][0] = 1;
REP(S, 1 << n) if(__builtin_popcount(S) > 1) FOR(i, 0, m) {
int u = lowbit(S);
for(int T = S; T; T = (T - 1) & S) if(T & u) FOR(j, 0, i)
f[S][i] += g[T][j] * C[s[S ^ T]][i - j];
g[S][i] = C[s[S]][i] - f[S][i];
}
double ans = 0;
FOR(i, 0, m) ans += (double) f[(1 << n) - 1][i] / C[m][i];
cout << fixed << setprecision(6);
cout << ans / (m + 1) << endl;
}
[ZJOI2015] 醉熏熏的幻想乡
考虑网络流,但是费用是一个二次函数,并不好做,考虑对流量求导来降次。
设函数 为流过了 的流量时的瞬时费用,最后把 积回去即可。
这个 太难算了,但是根据费用流的算法,是每次找费用最小的路进行增广,而这个最小费用随着流量的增加而增加,所以这个 就相当于当前的最小费用是多少。
考虑 的反函数 表示此时用的瞬时最大费用为 ,经过的总流量是多少,不难发现这个比较好算:对费用 求导得 ,那么瞬时最大费用为 时,这条边的流量限制即为 ,直接在实数域跑最大流就是结果。
现在能 后,就进行观察函数,发现 由 连续线性函数组成,在 处有断点,且连续部分是凸的。
是连续线性函数组成也很好证明,因为 就是线性函数。不难发现在跑最大流的同时,可以用判断当前的满流是被 限制还是被 限制,来算出当前 的线性函数,而且计算出来的直接是分数。
那么函数在 处断掉的原因也显然易见了,就是出现了新的合法边。
接下来就是求出这个凸壳的分割点,不难发现直接分治即可,计算当前两条直线的交点,并算该点的线性函数,若与这两个直线都不同,则有新直线,继续分治,否则就直接记录分割点退出即可。
求出凸壳之后就直接算积分即可,而积分即为函数下面积,直接计算即可。注意几个断点的特判即可。
时间复杂度 , 为一次网络流的复杂度。
ケロシの代码
const int N = 1e2 + 5;
const int INF = 1e9 + 7;
const double EPS = 1e-7;
const double FEPS = 1e-8;
int n, m, a[N], b[N], c[N], d[N], e[N][N];
namespace Dinic {
const int N = 2e3 + 5;
const int M = 1e5 + 5;
int S, T;
struct Edge {
int ne, to;
double ew;
} e[M]; int fi[N], c[N], ecnt;
int d[N];
void init() {
memset(fi, 0, sizeof fi);
ecnt = 1;
}
void add(int u, int v, double w) {
e[++ ecnt] = {fi[u], v, w};
fi[u] = ecnt;
e[++ ecnt] = {fi[v], u, 0};
fi[v] = ecnt;
}
bool bfs() {
memset(d, - 1, sizeof d);
queue<int> q;
d[S] = 0; q.push(S);
while(! q.empty()) {
int u = q.front();
q.pop();
for(int i = fi[u]; i; i = e[i].ne) if(e[i].ew > FEPS) {
int v = e[i].to;
if(d[v] == - 1) {
d[v] = d[u] + 1;
q.push(v);
}
}
}
return d[T] != - 1;
}
double dfs(int u, double w) {
if(u == T || w < FEPS) return w;
double res = 0;
for(int & i = c[u]; i; i = e[i].ne) {
int v = e[i].to;
if(d[v] != d[u] + 1) continue;
double val = dfs(v, min(w, e[i].ew));
if(val < FEPS) continue;
e[i].ew -= val;
e[i ^ 1].ew += val;
res += val;
w -= val;
if(w < FEPS) return res;
}
return res;
}
double dinic(int _S, int _T) {
S = _S, T = _T;
double res = 0;
while(bfs()) {
memcpy(c, fi, sizeof c);
res += dfs(S, INF);
}
return res;
}
}
ll gcd(ll x, ll y) {
if(! y) return x;
return gcd(y, x % y);
}
struct Fint {
ll x, y;
Fint(ll _x = 0, ll _y = 1) {
ll g = gcd(_x, _y);
x = _x / g, y = _y / g;
}
bool operator == (const Fint & A) const {
return x * A.y == y * A.x;
}
Fint operator + (const Fint & A) const {
return Fint(x * A.y + y * A.x, y * A.y);
}
Fint operator - (const Fint & A) const {
return Fint(x * A.y - y * A.x, y * A.y);
}
Fint operator * (const Fint & A) const {
return Fint(x * A.x, y * A.y);
}
Fint operator / (const Fint & A) const {
return Fint(x * A.y, y * A.x);
}
double get() {
return (double) x / y;
}
friend ostream & operator << (ostream & os, Fint A) {
return os << A.x << '/' << A.y;
}
};
struct Line {
Fint k, b;
Fint get(Fint x) {
return k * x + b;
}
bool operator == (const Line & A) const {
return k == A.k && b == A.b;
}
};
Line flow(double cost) {
int S = 0, T = n + m + 1;
Dinic :: init();
FOR(i, 1, n) if(b[i] < cost) {
if(! a[i]) Dinic :: add(S, i, c[i]);
else Dinic :: add(S, i, min((double) c[i], (cost - b[i]) / 2. / a[i]));
}
FOR(i, 1, n) FOR(j, 1, m) if(e[i][j])
Dinic :: add(i, n + j, INF);
FOR(i, 1, m) Dinic :: add(n + i, T, d[i]);
Dinic :: dinic(S, T);
Fint K, B;
FOR(i, 1, n) if(b[i] < cost && Dinic :: d[i] == - 1) {
if(! a[i]) B = B + c[i];
else if(a[i] * c[i] * 2 + b[i] < cost) B = B + c[i];
else K = K + Fint(1, a[i] * 2), B = B - Fint(b[i], a[i] * 2);
}
FOR(i, 1, m) if(Dinic :: d[n + i] != - 1) B = B + d[i];
return {K, B};
}
vector<Fint> S;
void slv(Line l, Line r) {
if(l == r) return;
Fint cost = (r.b - l.b) / (l.k - r.k);
Line mid = flow(cost.get() + EPS);
if(mid == r) S.push_back(cost);
else slv(l, mid), slv(mid, r);
}
void solve() {
cin >> n >> m;
FOR(i, 1, n) cin >> a[i] >> b[i] >> c[i];
FOR(i, 1, m) cin >> d[i];
FOR(i, 1, n) FOR(j, 1, m) cin >> e[i][j];
cout << flow(INF).b.get() << endl;
S.push_back(0);
FOR(i, 1, 3) {
slv(flow(i - 1 + EPS), flow(i - EPS));
S.push_back(i);
}
slv(flow(3 + EPS), flow(INF));
Fint ans;
FOR(i, 1, SZ(S) - 1) {
auto l = flow(S[i].get() - EPS);
auto r = flow(S[i].get() + EPS);
ans = ans + S[i] * (r.get(S[i]) - l.get(S[i]));
ans = ans + (S[i] + S[i - 1]) * (l.get(S[i]) - l.get(S[i - 1])) / 2;
}
cout << ans << endl;
}
[ZJOI2016] 小星星
考虑 dp,设 为 子树中,选了集合 ,且点 对应图上的点 的方案,那么直接转移是 的,无法通过。
瓶颈在于枚举子集,所以考虑若不强制点对应关系是一个排列,即使得一个树上的点可以对应多个图上的点,这样状态就不用记录选点集合,那么直接设 ,且转移非常简单。
但是这样会有不合法的方案,直接钦定不选一些点进行容斥即可。
时间复杂度 。
ケロシの代码
const int N = 17;
int n, m, e[N][N], g[N][N];
ull dp[N][N];
void dfs(int u, int fa, int S) {
REP(i, n) dp[u][i] = (S >> i & 1);
REP(v, n) if(e[u][v] && v != fa) {
dfs(v, u, S);
REP(i, n) if(S >> i & 1) {
ull res = 0;
REP(j, n) if(S >> j & 1) if(g[i][j]) {
res += dp[v][j];
}
dp[u][i] *= res;
}
}
}
void solve() {
cin >> n >> m;
REP(_, m) {
int u, v;
cin >> u >> v;
u --; v --;
g[u][v] = g[v][u] = 1;
}
REP(_, n - 1) {
int u, v;
cin >> u >> v;
u --; v --;
e[u][v] = e[v][u] = 1;
}
ull ans = 0;
dfs(0, 0, 0);
FOR(S, 1, (1 << n)) {
ull res = 0;
dfs(0, - 1, S);
REP(i, n) if(S >> i & 1) res += dp[0][i];
if((n - __builtin_popcount(S)) % 2) ans -= res;
else ans += res;
}
cout << ans << endl;
}
[ZJOI2016] 旅行者
由于图是一个网格图,比较特殊,所以考虑分治。
每次把矩形按照长的边经行分治,对于这条分治的分割线,从上面每个点跑一边最短路,这样就能计算出所有经过了这条分割线的最短路的贡献。
分割点贡献计算完后,两边就独立了,继续往下分治即可。
时间复杂度 。
ケロシの代码
const int N = 2e5 + 5;
const int INF = 1e9 + 7;
int n, m, q, a[N], b[N];
PII e[N][4];
struct Query {
int x1, y1, x2, y2, i;
} qs[N], q1[N], q2[N], q3[N];
int ans[N];
priority_queue<PII, vector<PII>, greater<PII>> pq;
int d[N], vis[N];
int gp(int x, int y) {
return (x - 1) * m + y;
}
void dij(int l1, int r1, int l2, int r2, int S) {
FOR(x, l1, r1) FOR(y, l2, r2) d[gp(x, y)] = INF;
FOR(x, l1, r1) FOR(y, l2, r2) vis[gp(x, y)] = 0;
d[S] = 0; pq.push({0, S});
while(! pq.empty()) {
int u = SE(pq.top());
pq.pop();
if(vis[u]) continue;
vis[u] = 1;
REP(i, 4) {
int v, w; tie(v, w) = e[u][i];
if(v > INF) continue;
if(d[v] > d[u] + w) {
d[v] = d[u] + w;
pq.push({d[v], v});
}
}
}
FOR(x, l1, r1) FOR(y, l2, r2) vis[gp(x, y)] = 1;
}
void slv(int l1, int r1, int l2, int r2, int ql, int qr) {
if(l1 > r1 || l2 > r2 || ql > qr) return;
if(r1 - l1 > r2 - l2) {
int mid = l1 + r1 >> 1;
FOR(i, l2, r2) {
dij(l1, r1, l2, r2, gp(mid, i));
FOR(i, ql, qr) chmin(ans[qs[i].i], d[gp(qs[i].x1, qs[i].y1)] + d[gp(qs[i].x2, qs[i].y2)]);
}
int t1 = 0, t2 = 0;
FOR(i, ql, qr) {
if(qs[i].x1 < mid && qs[i].x2 < mid) q1[++ t1] = qs[i];
if(qs[i].x1 > mid && qs[i].x2 > mid) q2[++ t2] = qs[i];
}
int tp = ql;
FOR(i, 1, t1) qs[tp ++] = q1[i];
FOR(i, 1, t2) qs[tp ++] = q2[i];
slv(l1, mid - 1, l2, r2, ql, ql + t1 - 1);
slv(mid + 1, r1, l2, r2, ql + t1, ql + t1 + t2 - 1);
}
else {
int mid = l2 + r2 >> 1;
FOR(i, l1, r1) {
dij(l1, r1, l2, r2, gp(i, mid));
FOR(i, ql, qr) chmin(ans[qs[i].i], d[gp(qs[i].x1, qs[i].y1)] + d[gp(qs[i].x2, qs[i].y2)]);
}
int t1 = 0, t2 = 0;
FOR(i, ql, qr) {
if(qs[i].y1 < mid && qs[i].y2 < mid) q1[++ t1] = qs[i];
if(qs[i].y1 > mid && qs[i].y2 > mid) q2[++ t2] = qs[i];
}
int tp = ql;
FOR(i, 1, t1) qs[tp ++] = q1[i];
FOR(i, 1, t2) qs[tp ++] = q2[i];
slv(l1, r1, l2, mid, ql, ql + t1 - 1);
slv(l1, r1, mid + 1, r2, ql + t1, ql + t1 + t2 - 1);
}
}
void solve() {
cin >> n >> m;
FOR(i, 1, n) FOR(j, 1, m - 1) cin >> a[gp(i, j)];
FOR(i, 1, n - 1) FOR(j, 1, m) cin >> b[gp(i, j)];
memset(e, 0x3f, sizeof e);
FOR(i, 1, n) FOR(j, 1, m - 1) {
e[gp(i, j)][0] = {gp(i, j + 1), a[gp(i, j)]};
e[gp(i, j + 1)][1] = {gp(i, j), a[gp(i, j)]};
}
FOR(i, 1, n - 1) FOR(j, 1, m) {
e[gp(i, j)][2] = {gp(i + 1, j), b[gp(i, j)]};
e[gp(i + 1, j)][3] = {gp(i, j), b[gp(i, j)]};
}
cin >> q;
FOR(i, 1, q) {
cin >> qs[i].x1 >> qs[i].y1 >> qs[i].x2 >> qs[i].y2;
qs[i].i = i;
ans[i] = INF;
}
FOR(i, 1, n) FOR(j, 1, m) vis[gp(i, j)] = 1;
slv(1, n, 1, m, 1, q);
FOR(i, 1, q) cout << ans[i] << endl;
}
[ZJOI2016] 线段树
对于这种取 的问题,首先要考虑 序列怎么做。不难想到 dp 计算极长 段的方案数,设 为 为极长 段,也就是 和 为 , 中的数都为 ,的方案数,不难列出转移方程:
接下来要考虑非 序列的情况,不难想到把序列中 的设为 ,把 的设成 ,这样就能算出 的极长 段的方案数了,设这个为 。
然后就能统计答案了:
因为输入的数据随机,所以有用的值就期望 个,所以时间复杂度 。
但是还能做的更优秀。对于上述的式子,不难发现 的贡献为 ,其它的每个 的贡献都为 。
而上述对于每个 的 dp,转移都一样且互不干扰,所以直接把每个 和贡献一起丢进去 dp 即可。
时间复杂度 。
ケロシの代码
const int N = 4e2 + 5;
const int P = 1e9 + 7;
const int INF = 1e9 + 7;
int add(int x, int y) { return (x + y < P ? x + y : x + y - P); }
void Add(int & x, int y) { x = (x + y < P ? x + y : x + y - P); }
int sub(int x, int y) { return (x < y ? x - y + P : x - y); }
void Sub(int & x, int y) { x = (x < y ? x - y + P : x - y); }
int mul(int x, int y) { return (1ll * x * y) % P; }
void Mul(int & x, int y) { x = (1ll * x * y) % P; }
int n, m, a[N];
int dp[N][N], b[N][N], f[N][N], g[N][N];
int F(int x) {
return mul(mul(x, x + 1), (P + 1) / 2);
}
void solve() {
cin >> n >> m;
FOR(i, 1, n) cin >> a[i];
a[0] = a[n + 1] = INF;
FOR(l, 1, n) {
int res = 0;
FOR(r, l, n) {
chmax(res, a[r]);
if(res < a[l - 1] && res < a[r + 1])
dp[l][r] = sub(res, (l == 1 && r == n ? 0 : min(a[l - 1], a[r + 1])));
b[l][r] = add(add(F(l - 1), F(n - r)), F(r - l + 1));
}
}
REP(_, m) {
FOR(l, 1, n) FOR(r, l, n) f[l][r] = add(f[l - 1][r], mul(dp[l][r], l - 1));
ROF(r, n, 1) ROF(l, r, 1) g[l][r] = add(g[l][r + 1], mul(dp[l][r], n - r));
FOR(l, 1, n) FOR(r, l, n) {
Mul(dp[l][r], b[l][r]);
Add(dp[l][r], f[l - 1][r]);
Add(dp[l][r], g[l][r + 1]);
}
}
FOR(i, 1, n) {
int res = 0;
FOR(l, 1, i) FOR(r, i, n)
Add(res, dp[l][r]);
cout << res << " ";
}
cout << endl;
}
[ZJOI2016] 随机树生成器
考虑提取一些特征,然后进行区分,这一步非常困难。
先分方法三和方法四,考虑横轴为树的直径长度,纵轴为 。
把点都用 python 的 matplotlib 画出来,便于观察与计算。
计算分割线为 :
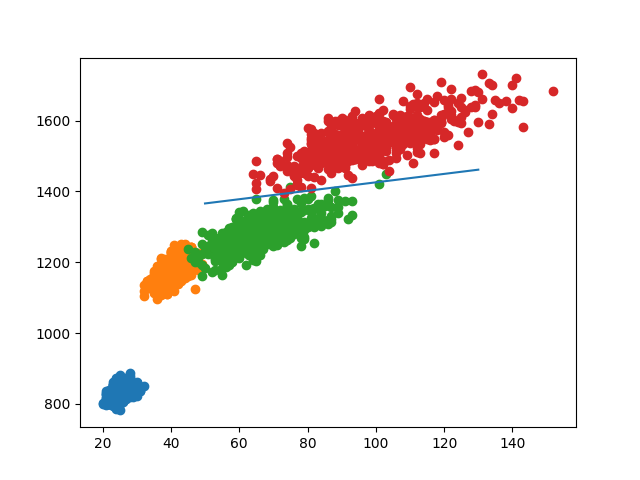
然后是分方法三和方法二,考虑横轴为树的直径长度,纵轴为每个点到树上最远点的距离和。
计算分割线为 :
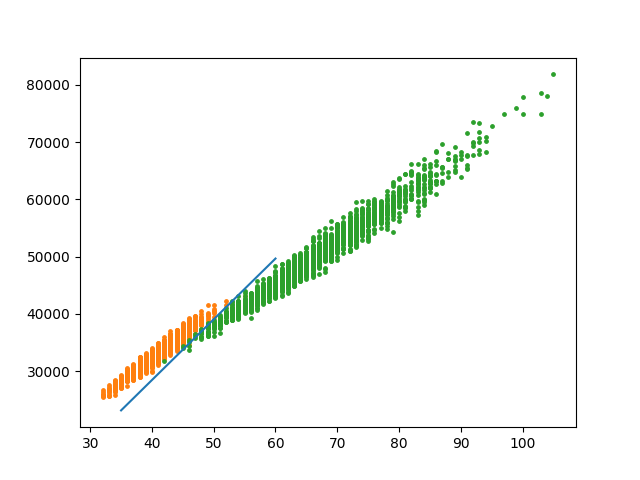
时间复杂度 。
ケロシの代码
const int N = 1e3 + 5;
int I, m, n;
int fi[N], ne[N << 1], to[N << 1], ecnt;
int rt, d[N], sz[N], f[N];
void add(int u, int v) {
ne[++ ecnt] = fi[u];
to[ecnt] = v;
fi[u] = ecnt;
}
void dfs(int u, int fa) {
if(d[u] > d[rt]) rt = u;
sz[u] = 1;
for(int i = fi[u]; i; i = ne[i]) {
int v = to[i];
if(v == fa) continue;
d[v] = d[u] + 1;
dfs(v, u);
sz[u] += sz[v];
}
}
void solve() {
cin >> I >> m; n = 1000;
REP(_, m) {
FOR(i, 1, n) fi[i] = f[i] = 0; ecnt = 0;
REP(_, n - 1) {
int u, v;
cin >> u >> v;
add(u, v); add(v, u);
}
rt = 1;
d[rt] = 0; dfs(rt, 0);
d[rt] = 0; dfs(rt, 0);
FOR(i, 1, n) chmax(f[i], d[i]);
d[rt] = 0; dfs(rt, 0);
FOR(i, 1, n) chmax(f[i], d[i]);
double res = 0, sum = 0;
FOR(i, 1, n) res += log(sz[i]);
FOR(i, 1, n) sum += f[i];
if(res < 1000)
cout << 1 << endl;
else if(I >= 3 && res > d[rt] * 1.1923 + 1306.3077)
cout << 4 << endl;
else if(I == 1 || (I != 3 && sum > d[rt] * 1061.25 - 14007.5))
cout << 2 << endl;
else
cout << 3 << endl;
}
}
[ZJOI2016] 大森林
考虑几个操作都不会影响查询的结果,可以离线做。
所以考虑离线,并把所有的点挂到一棵树上,从左往右扫,以维护出当前的树,然后查询。
但是改生长节点的时候,区间内可能会有树没有这个点,但是不难发现有这个点的树是一段区间,所以直接把修改缩到每棵树有这个点的区间即可。
不难发现一个修改生长点操作就相当于把后面的一些新点集体换了父亲,那么离线的时候在扫到 时集体换父亲,在扫到 时换回来即可。
但是集体换父亲的操作不好直接做,考虑建立虚点,每次添加点的操作,就挂到上一个虚点下面。每次改生成节点操作,建立新虚点,并挂到上一个虚点下面,表示没换父亲时继承上一个生长节点,每次换父亲就直接把这个虚点的父亲换掉即可。
使用 LCT 维护换父亲操作即可。
时间复杂度
ケロシの代码
const int N = 3e5 + 5;
int n, q, pl[N], pr[N];
int t[N], p[N], tot, lst;
vector<array<int, 4>> e;
int ans[N];
int ch[N][2], f[N];
int a[N], F[N];
void pushup(int u) {
F[u] = F[ch[u][0]] + F[ch[u][1]] + a[u];
}
int get(int u) {
return ch[f[u]][1] == u;
}
bool isroot(int u) {
return ch[f[u]][0] != u && ch[f[u]][1] != u;
}
void rotate(int u) {
int y = f[u], z = f[y], o = get(u);
if(! isroot(y)) ch[z][get(y)] = u;
ch[y][o] = ch[u][o ^ 1];
f[ch[u][o ^ 1]] = y;
ch[u][o ^ 1] = y;
f[y] = u; f[u] = z;
pushup(y); pushup(u);
}
void splay(int u) {
for(int fa; fa = f[u], ! isroot(u); rotate(u)) {
if(! isroot(fa))
rotate(get(fa) == get(u) ? fa : u);
}
}
int access(int u) {
int p = 0;
for(; u; p = u, u = f[u]) {
splay(u);
ch[u][1] = p;
pushup(u);
}
return p;
}
int lca(int u, int v) {
access(u);
return access(v);
}
int dep(int u) {
access(u);
splay(u);
return F[u];
}
void link(int u, int v) {
f[u] = v;
}
void cut(int u) {
access(u);
splay(u);
f[ch[u][0]] = 0;
ch[u][0] = 0;
pushup(u);
}
int query(int u, int v) {
int mid = lca(u, v);
return dep(u) + dep(v) - dep(mid) * 2;
}
void solve() {
cin >> n >> q;
tot ++, lst = q + 1;
pl[tot] = 1, pr[tot] = n;
a[tot] = F[tot] = 1;
link(lst, tot);
FOR(i, 1, q) {
int opt; cin >> opt;
if(opt == 0) {
int l, r;
cin >> l >> r;
tot ++;
pl[tot] = l, pr[tot] = r;
a[tot] = F[tot] = 1;
link(tot, lst);
}
if(opt == 1) {
int l, r, x;
cin >> l >> r >> x;
chmax(l, pl[x]);
chmin(r, pr[x]);
if(l > r) continue;
lst ++;
link(lst, lst - 1);
e.push_back({l, 0, lst, x});
e.push_back({r + 1, 0, lst, lst - 1});
}
if(opt == 2) {
int x, u, v;
cin >> x >> u >> v;
e.push_back({x, i, u, v});
}
}
sort(ALL(e));
FOR(i, 1, q) ans[i] = - 1;
for(auto h : e) {
if(h[1]) {
ans[h[1]] = query(h[2], h[3]);
}
else {
cut(h[2]);
link(h[2], h[3]);
}
}
FOR(i, 1, q) if(ans[i] != - 1) cout << ans[i] << endl;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 如何调用 DeepSeek 的自然语言处理 API 接口并集成到在线客服系统
· 【译】Visual Studio 中新的强大生产力特性
· 2025年我用 Compose 写了一个 Todo App