KD Tree

最近在项目中用到了，特地搬运过来。

Kd-树 其实是K-dimension tree的缩写，是对数据点在k维空间中划分的一种数据结构。其实，Kd-树是一种平衡二叉树。

举一示例：

假设有六个二维数据点 = {（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，数据点位于二维空间中。为了能有效的找到最近邻，Kd-树采用分而治之的思想，即将整个空间划分为几个小部分。六个二维数据点生成的Kd-树的图为：

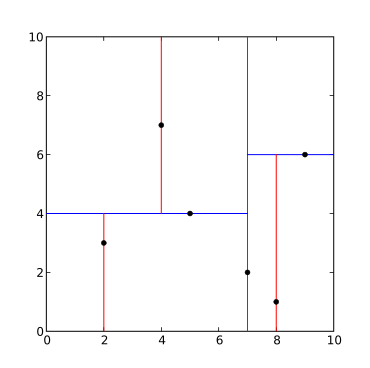
                          图1                                                                                           图2

 

而在三维空间中，则是这个样子的

对于拥有n个已知点的kD-Tree，其复杂度如下：

1. 构建：O(log²n)
2. 插入：O(log n)
3. 删除：O(log n)
4. 查询：O(n^1-1/k+m) m---每次要搜索的最近点个数

 Kd-树的构建

Kd-树是一个二叉树，每个节点表示的是一个空间范围。下表表示的是Kd-树中每个节点中主要包含的数据结构。Range域表示的是节点包含的空间范围。Node-data域就是数据集中的某一个n维数据点。分割超面是通过数据点Node-Data并垂直于轴split的平面，分割超面将整个空间分割成两个子空间。令split域的值为i，如果空间Range中某个数据点的第i维数据小于Node-Data[i]，那么，它就属于该节点空间的左子空间，否则就属于右子空间。Left，Right域分别表示由左子空间和右子空间空的数据点构成的Kd-树。

 

域名	数据类型	描述
Node-Data	数据矢量	数据集中某个数据点，是n维矢量
Range	空间矢量	该节点所代表的空间范围
Split	整数	垂直于分割超面的方向轴序号
Left	Kd-tree	由位于该节点分割超面左子空间内所有数据点构成的Kd-树
Right	Kd-tree	由位于该节点分割超面左子空间内所有数据点构成的Kd-树
Parent	Kd-tree	父节点

构建Kd-树的伪码为：

算法：构建Kd-tree

输入：数据点集Data_Set，和其所在的空间。

输出：Kd，类型为Kd-tree

1 if data-set is null ,return 空的Kd-tree

2 调用节点生成程序

 （1）确定split域：对于所有描述子数据（特征矢量），统计他们在每个维度上的数据方差，挑选出方差中最大值，对应的维就是split域的值。数据方差大说明沿该坐标轴方向上数据点分散的比较开。这个方向上，进行数据分割可以获得最好的分辨率。

（2）确定Node-Data域，数据点集Data-Set按照第split维的值排序，位于正中间的那个数据点 被选为Node-Data，Data-Set` =Data-Set\Node-data

3 dataleft = {d 属于Data-Set` & d[:split]<=Node-data[:split]}

   Left-Range ={Range && dataleft}

  dataright = {d 属于Data-Set` & d[:split]>Node-data[:split]}

  Right-Range ={Range && dataright}

4：left = 由（dataleft,LeftRange）建立的Kd-tree

   设置:left的parent域（父节点）为Kd

  ：right = 由（dataright,RightRange）建立的Kd-tree

  设置：right的parent域为kd。

如上例中，

（1）确定：split 域=x，6个数据点在x,y 维度上的数据方差为39,28.63.在x轴方向上的方差大，所以split域值为x。

（2）确定：Node-Data=（7,2），根据x维上的值将数据排序，6个数据的中值为7，所以node-data域为数据点（7,2）。这样该节点的分割超面就是通过（7,2）并垂直于：split=x轴的直线x=7.

（3）左子空间和右子空间，分割超面x=7将整个空间分为两部分。x<=7 为左子空间，包含节点（2,3），（5,4），（4，7），另一部分为右子空间。包含节点（9,6），（8,1）

 

这个构建过程是一个递归过程。重复上述过程，直至只包含一个节点。