泊松分布（Poisson distribution）的简单认识

泊松分布是从二项分布而来的，在二项分布的伯努力试验中，如果试验次数n很大，二项分布的概率p很小，且乘积λ= n p比较适中，则事件出现的次数的概率可以用泊松分布来逼近。

说明两点：

1.泊松分布是离散型概率分布，表示（固定尺度的）连续区间（如时间，距离）上给定的事件发生次数的概率，所以可以看做泊松分布中n是无穷大的。二项分布是固定实验次数下，事件发生次数的概率，n是有界的。

2.泊松分布中发生次数的期望是固定的 λ，事件发生的概率p不定，p=λ/n；二项分布中事件发生的概率p是固定的，发生次数的期望不定，λ=n*p。

 

由二项分布的概率质量公式推导泊松分布的概率质量公式。

（源自：维基百科）

首先，回顾e的定义：

\lim_{n\to\infty}\left(1-{\lambda \over n}\right)^n=e^{-\lambda},

二项分布的定义：

P(X=k)={n \choose k} p^k (1-p)^{n-k}.

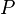如果令p = \lambda/n, n趋于无穷时P的极限:

\begin{align}\lim_{n\to\infty} P(X=k)&=\lim_{n\to\infty}{n \choose k} p^k (1-p)^{n-k} \\ &=\lim_{n\to\infty}{n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}\\&=\lim_{n\to\infty}\underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}_F\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \lim_{n\to\infty}\underbrace{\left[ \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots \left(1-\frac{k-1}{n}\right) \right]}_{\to 1}\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)\end{align}

posted on 2012-06-24 13:47  NLP新手  阅读(27533)  评论(4)    收藏  举报

导航