Histogram Equalization（直方图均衡化）

（源自：百度百科）

　　图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。直方图拉伸是通过对比度拉伸对直方图进行调整，从而“扩大”前景和背景灰度的差别，以达到增强对比度的目的，这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。

 　　直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。

 

（源自：维基百科）

纵览

这种方法通常用来增加许多图像的全局对比度，尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法，亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。

这种方法对于背景和前景都太亮或者太暗的图像非常有用，这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作，如果已知均衡化函数，那么就可以恢复原始的直方图，并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择，它可能会增加背景噪声的对比度并且降低有用信号的对比度。

实现

我们来看一个灰度图像，让表示灰度出现的次数，这样图像中灰度为 的像素的出现概率是

 是图像中所有的灰度数， 是图像中所有的像素数,  实际上是图像的直方图，归一化到 。

把  作为对应于  的累计概率函数, 定义为：

 是图像的累计归一化直方图。

我们创建一个形式为 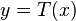 的变化，对于原始图像中的每个值它就产生一个 ，这样  的累计概率函数就可以在所有值范围内进行线性化，转换公式定义为：

注意 T 将不同的等级映射到  域，为了将这些值映射回它们最初的域，需要在结果上应用下面的简单变换：