KMP算法的详细解释

什么是kmp算法呢？这是一个处理字符串的算法，用来判断给出的模式串p是否存在于文本串t中（p的长度小于t）。

在本文中，字符串储存在字符数组中，并且第一个字符放在下标为1的元素中。

那么如何理解kmp算法呢？首先要从最朴素的匹配算法说起。

我们判断p是否存在于t中，最原始的方法就是从头到尾一直遍历。定义变量i为文本串t中的下标，定义变量j为模式串p中的下标，然后i表示看文本串的前i个字符，j表示判断这前i个字符组成的子串中，长度为j的前后缀是否相等。

如果t[i] = p[j]，则i与j同时后移一位，比较下一位是否相同，如果t[i] != p[j]，则表示串t在i位置处“失配”，需要重新进行匹配，i保持不动，并且j必须返回到模式串p的开头，也就是相当于回退到1，然后再次进行循环。

如果t的长度为m，p的长度为n时，这样做的时间复杂度为O(m*n)

kmp就是在这种最原始匹配算法的基础之上的改进算法。

Kmp的改进之处在哪里呢？ 上面这种复杂度最大的朴素方法中，有一个步骤，当“失配”时，我们的i不移动，但是j需要回到串p的开头，这样每一次失配，我们都需要再从模式串的开头重新开始匹配，相当于将j直接回退到1，然后再从1开始去试满足的最大的相同前后缀长度，多了好多次循环，聪明的科学家们想到的办法是：假设现在有这样一种情况：

在遍历到文本串t的的前i-1个字符组成的子串之后，我们已经确定了该子串中的长度为j-1的前后缀是相同的，那么现在在考虑下一个字符（第a个）时发生失配，也就是第a个字符不等于第b个，我们不想让b直接回退到1，而是回退到1和b之间的某个值，以减小复杂度。

我们先放下这个问题，思考另外一个问题：

如果要求一个字符串中相同的前缀和后缀的最长长度，怎么求呢？

和上面的kmp其实特别像，还是分治的思想：假设我们现在已经看到了字符串的前i-1个元素，并且在这i-1个元素的子串中，长度为j-1的后缀和前缀是一样的，表示匹配到了j-1的长度，那么我们就可以考虑第字符串中第i个元素是否和第j个元素相同了，如果相同就继续匹配下去，如果不同，j仍要回退，但是不能把j直接回退到1然后递增地去判断，这样复杂度太大。

因为我们现在知道的条件是前i-1个字符组成的子串的长度为j-1的前缀和后缀是相同的，那么如果这个长度为j-1的前缀的某个长度（假设为b）的前缀恰好等于其后缀的后缀，那么就表示我们可以对于长度i-1的子串，去考虑其长度为b+1的前后缀是否相等了，换言之，j不回退到1了，而是回退到b+1，因为在这种情况下我们是知道a-1的子串中，长度为c的前后缀也是相同的。

觉得上面这段话难理解的话，我来举一个实际一点的例子帮助理解。

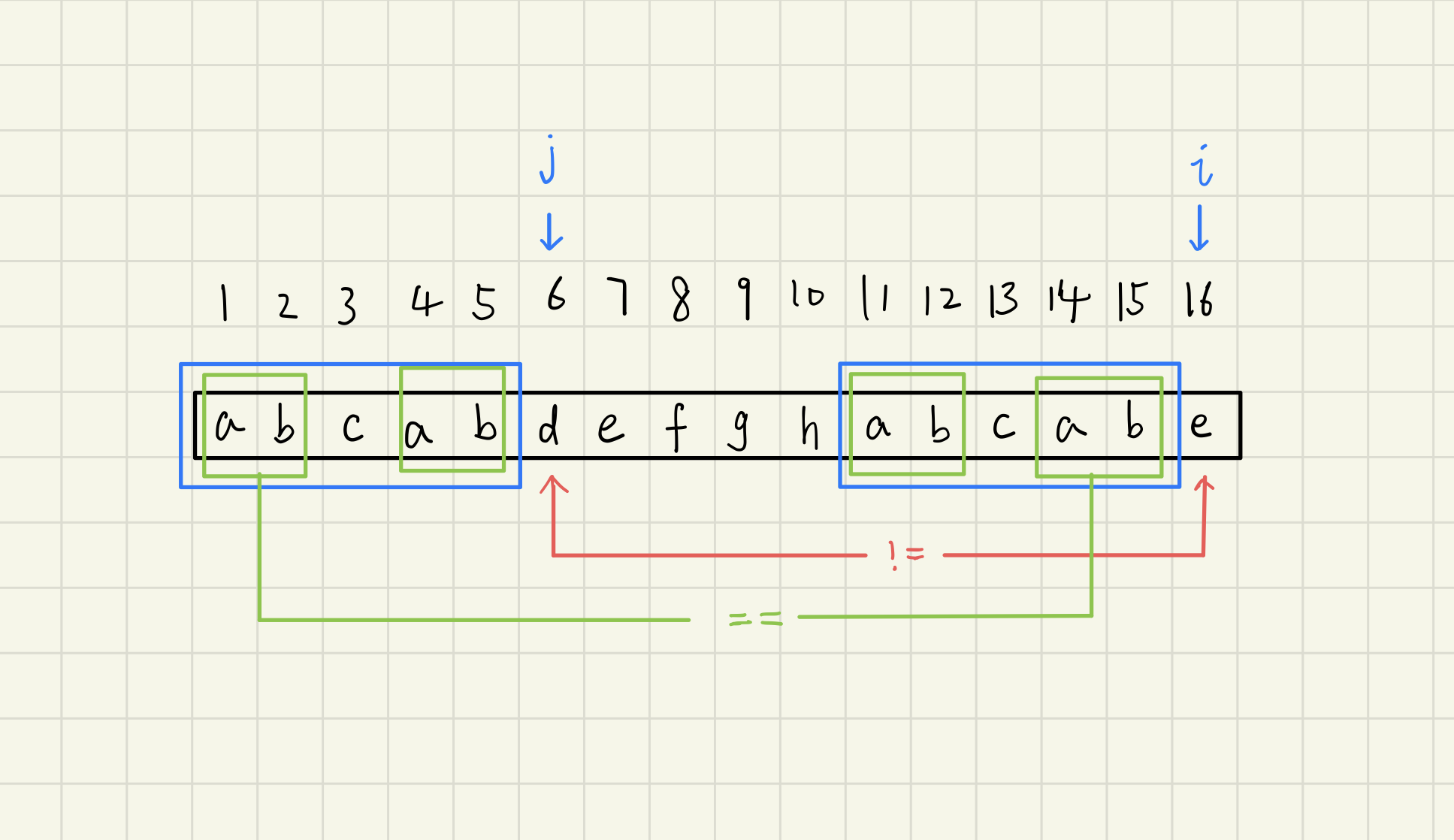
上图中，假设现在是i=16，j=6，表明前面我们已经确定了前15个字符的子串中，相同的前缀和后缀的长度为5，现在新增了第16个字符，我们来考虑第6个和第16个字符是否相同.

如图，明显不同，所以我们这个时候就没办法说长度为16的子串中相同的前后缀长度为6了，那么这个前后缀的长度是多少呢？要靠j的移动来判断。

前面也说了，不能用朴素算法将j先回退到1，然后再自增j来判断。

我们发现在这个例子中，恰好长度为5的前缀abcab，在这个前缀内部，自己也是有前缀和后缀相等的情况的，前两个ab等于后两个ab，那么这样就是说长度为15的子串中，其实有“长度为5的前缀的长度为2的前缀“ = ”长度为5的后缀的长度为2 的后缀“ ，也就是说，长度为15的子串中，最长的相等的前后缀是5，但是我们根据长度为5的前缀自身也有相等的前后缀的情况（本质上是递归嘛）找到了长度为长度为15的子串中，次长的相等的前后缀长度是2，那么就将j回退到2的下一个位置，也就是3，再次判断，这时回退的时候是判断第三个字符和第16个字符，这个情况在前面没有判断过，说不定就相等了呢？要是不相等，就再次回退。用这种方法去回退，就不用将j回退到1，然后再自增，从而减小复杂度了。

这里的递归的思想其实很巧妙，我的j回退到哪呢？我已经知道了前i-1个字符中有长度为j-1 的前后缀是相同的，那么我去看是否有前缀的前缀等于后缀的后缀，也就是说，这i-1个字符中是否还有长度更小（小于j-1）的前后缀是相等的，方便我把j回退到那里去，因为前后缀这个性质，所以我要实现上面那个目的，其实只需要去看长度为j-1的子串中，是否有前后缀相等就可以了。

那我们怎么”看“呢？总不能每次都去求你这个前缀里面是否还有前后缀相等吧。我们可以用打表的方式，提前做出一个next数组，它的下标从1 开始，next[t] 里面放的就是 “前t-1个字符组成的子串中的相等的前缀和后缀的长度再+1 ”。加一是为了方便在j回退的时候，直接赋值给j。

简而言之，利用的就是”前缀有可能有某个长度的前缀等于后缀的相同长度的后缀“这个性质，来减少j的回退步数，从而减少复杂度。

那怎么求这个next数组呢？

直接上代码吧。

next数组只跟模式串p有关，并且它的第一个元素下标从1开始。而且第i个需要表示与前i-1个字符组成的字串相关的内容，所以它的长度应该比模式串p的长度plen多1。

next[i]中元素的含义：前i-1个字符组成的子串中的最长的相同前缀和后缀的长度再加一。

//这个next的各个元素的填充也是从头到尾的，即从next[1]到next[ plen+1 ]。
//ch数组就是我们的字符串
void getnext(char * ch, int plen, int *next){
	next[1] = 0;	//首先前0个元素是没有的，所以next[1]是0
	int i=1,j=0;	//i是子串长度，也就是指向这个子串中的后缀的最后一个元素，j表示相同的前缀和后缀的长度，即指向子串中的前缀的最后一个元素。 
	while(i<=plen){
		if(j==0 || ch[i] == ch[j])
			next[++i] = ++j;
		else j = next[j]; 
	}
}

上面主要控制while循环的是i，当i为p的长度再加一，即plen+1时则说明已经把next从1填到了plen+1。就可以退出while循环。那么在每一次的循环中，有两个分支：

第一个分支，如果当前ch[i] == ch[j] （也就是模式串p中的长度为i的子串前缀的最后一个元素==后缀的最后一个元素）时那么就表示当前我们可以进入下一个循环，即考虑p的长度为i+1的字串的长度为j+1的前缀与后缀了，而且正好我们上文分析到的，next[i] 里面放的是“前i-1个字符组成的子串中的相等的前缀和后缀的长度再加一 ”。在这里面数组下标和数组的值都其实隐含着“+1”，所以有了next[++i] = ++j;

另外一个分支是ch[i] ！= ch[j]，表示模式串p中的长度为i的子串的长度为j的前缀和后缀是不匹配的（到了这最后一位不匹配了）。那么我们怎么办呢？回退咯，并且因为我们对于next[i]数组的巧妙定义，直接j = next[j]就完成了我们上面所说的回退。

那么还有一种特殊情况，是一开始的j=0，一开始next[2] 就将其置为1，因为第一个字符它只有一个，不构成子串，所以它的相等的前后缀长度为0，加上1就是1。所以我们在判断条件中加了一个“或j==0” ，就是为了在第一次循环中，将next[2]置为1；

其实这个生成next数组的过程，就是求字符串中相同的前后缀的长度的过程，两者其实本质上是一个东西，next数组生成完了，求字符串中相同的最长前后缀问题也就解决了，属于”你中有我，我中有你“。

解决了这个问题之后我们再来看kmp算法。

如果将模式串直接拼到文本串的前端，问题 ”判断给出的模式串p是否存在于文本串t中“ 也就转换成了 “判断拼接后的字符串中是否有一个子串的最大前后缀的长度与模式串的长度相等” 啦。

（如果你跟着我的引导，把前面的内容都看懂了，然后在看到这句话时有种醍醐灌顶的感觉，那么我会很开心）

kmp函数的具体代码如下，不用做真正的拼接操作，我们只需要将j指向模式串p，然后i指向文本串t就行了。

并且，生成的next数组，也只需要生成模式串p的长度就行了，生成多了没用啊。

//文本串text string，模式串pattern string
//i指向文本串，j指向模式串
int kmp(int *t,int tlen,int *p,int plen){
//	 int cnt = 0;
	int *next = new int [plen+2]; //多预留了一个空间，然后我顺手再给它开了一位的空间
	getnext(p,plen,next);   //生成next数组
	int j = 1;
	for(int i=1;i<=tlen;i++){
		while(j>1 && t[i] != p[j]){
			j = next[j];
		}
		if(t[i] == p[j]) j++;
		if(j == plen+1) return i-plen+1;
	}
	return -1;
} 

i指向文本串t，然后i从1开始向后推，就像本文一开始讲的那样，t[i]与p[j]开始匹配，然后一旦失配，j就“回溯”，若一次回溯后仍失配，则继续回溯直到j变成1。那若是t[i]与p[j]相等，就j后移并且进入下一次循环，也就是i也后移，然后当j到了plen+1的时候，就表示模式串p已找到（为什么是plen+1呢？因为第当plen个匹配完成后，j会再加一，所以当模式串p匹配完成时j的值应该是plen+1的） 然后返回的值也就是模式串p在文本串t中出现的位置的首个字符的下标，所以就是i减去模式串p的长度plen再加一。

其实kmp的整个过程可以模仿next来写，像这样： （但是下面这个还没验证对不对）

int kmp(int *t,int tlen,int *p,int plen){
	int *next = new int [plen+2];
	getnext(p,plen,next);
	int j = 0,i=1; 	
	while(i<=tlen){
		if(j == 0 || t[i] == p[j]){
			i++;
			j++;
		}
		else j = next[j];
		if(j == plen+1) return i-plen;
	}
	return -1;
}