第四次作业:文法和语言总结与梳理
1. 梳理第二章的内容,写一篇理解与总结。
第二章进入了尾声,我总结了一下本章的内容,其中包括文法的直观概念、符号和符号串、文法和语言的形式定义、文法的类型、上下文无关文法及语法树、句型的分析等这几个内容。
(1).上下文无关法
文法:是描述语言的语法结构的形式规则(即语法规则)。文法可以表示为四元组G=(VN,VT,P,S),其中VN为非终结符,VT 终结符的非空有穷集,VN∩VT=Φ,P为产生式(规则)集合,S称作识别符或开始符。
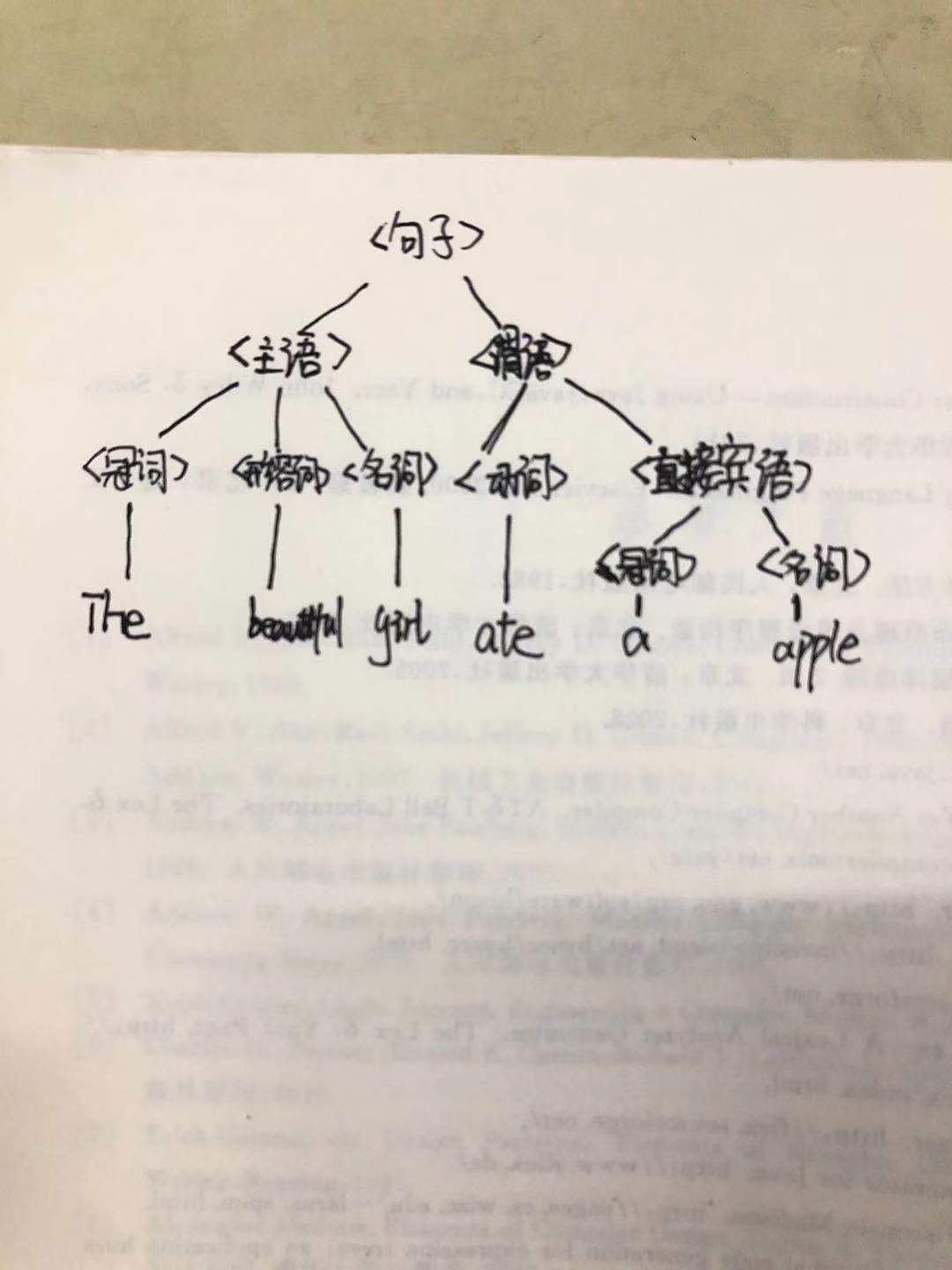
举例:The beautiful girl ate apple
规则:规则又叫产生式(productionrule),它是语法单位结构的一种表示,它引入了符号“::=”或“→”表示“由……组成”,上述句子的结构可以表示如下:
<句子> →<主语> <谓语>
<主语> → <冠词> <形容词> <名词>
<冠词>→The
<形容词>→beautiful
<谓语>→<动词> <直接宾语>
<动词> →ate
<直接宾语>→<冠词><名词>
<冠词> → a
<名词>→girl
<名词>→apple
句子的推导:用规则(产生式)按一定方式去推导或产生句子的过程。
<句子>=><主语> <谓语>
=><冠词> <形容词> <名词> <谓语>
=>The <形容词> <名词> <谓语>
=>The beautiful <名词> <谓语>
=>The beautiful girl <谓语>
=>The beautiful girl <动词> <直接宾语>
=>The beautiful girl ate <直接宾语>
=>The beautiful girl ate <冠词><名词>
=>The beautiful girl ate a <名词>
=>The beautiful girl ate a apple
语法树:句子结构的图形表示方式
(2)文法和语言的形式定义
定义1 产生式(或规则)是一有序对(A,α),通常写为:
A→ α或A∷= α
其中A是一个符号作为产生式左部,α为有穷符号串作为产生式的右部,“→”或“∷=”表示“定义为…”或“由…组成”。
定义2 文法是一个四元组:G[S]=(VN,VT, P, S)
其中:
VN为非终结符集合;
在规则左部出现的符号称为非终结符,它们的全体形成VN
VT为终结符集合;VN∩VT =Ф,一般令V=VN∪VT,V中的符号称为文法符号;(V字汇表)
在规则中只在右部出现的符号称为终结符,它们的全体形成VT
P为产生式集合;
P中的每个产生式写为:α→β或α∷=β。
S为开始符号(或称根符号,识别符号)。
文法所确定的语言为: L(G[Z])={anbn| n>=1}
(3)语法树和文法的二义性
语法树: 设文法G=(VN,VT,P,S) ,所谓语法树是一张图,这张图表示一个句型的推导过程。语法树结构是一棵倒立的树结构,其中,结点的名字N∈V,根结点的名字S是文法G的开始符号,树中的中间结点是句型推导过程中使用的非终结符,树的端末结点自左向右排列就是所给句型。
子树:由语法树的某个结点(子树的根)连同它下面发出的部分组成语法树的子树。只含有单层分支的子树为简单子树。
子树与短语:在句型所对应的语法树中,若某些符号按从左到右的顺序组成某棵子树的末端结点,那么由这些末端结点所组成的符号串是相对于子树根结点的短语。
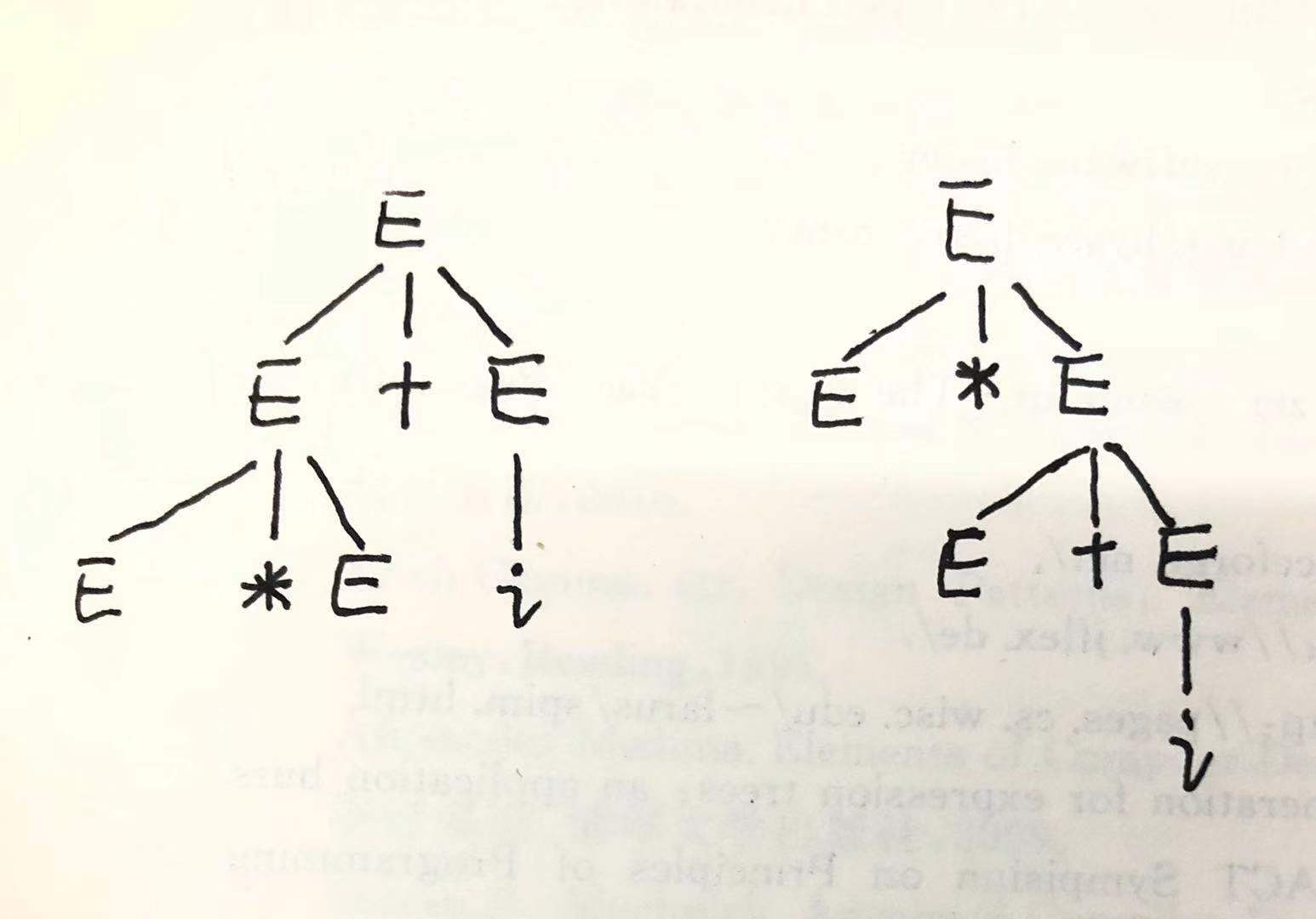
文法的二义性:若一个文法存在某个句子对应两棵不同的语法树,则称此文法是二义性文法,运用文法描述程序设计语言的语句成份,一般希望所给文法是非二义文法,但是,有时候采用二义性文法比非二义文法要简单的多,所以,经常用二义性文法描述程序设计语言。
举例子:文法G[E] :E→E+E | E*E | (E) | i
为符号串E*E+i构造语法树
2. 尝试写出PL/0 语言的文法。(或者你认为比较好的语言规则)
整数n: n->1|2|3|4|5|6|7|8|9|
标识符i: i-><字母> {<字母>|<数字>}
表达式e: e→ [+|-]<项>{<加减运算符><项>}
条件语句: <条件语句> -> if <条件> then <语句>
赋值语句: <赋值语句>→ <标识符>:=<表达式>
复合语句: <复合语句> → begin<语句>{;<语句>}end
函数: <函数>→<主函数><其他函数>|<主函数>
程序: <程序> -> <分程序>





