条件随机场(Conditional random field)
条件随机场真是把我给折磨坏了啊,本以为一本小小的《统计学习方法》攻坚剩下最后一章,心情还是十分愉悦的,打算一口气把它看完,结果真正啃起来真是无比的艰难啊,每一句对我都好像是天书一般,怎么这么多没有接触过的概念啊!什么无向图?什么最大团?搞什么鬼啊,真让人头大 现在想想可能就是被这些概念吓到了当时,等你仔细的弄懂了它们是什么意思,理解起来难度就会小很多啦,所以,我决定先从概念开始说起,捋顺一下思路,至于条件随机场先表过不谈!
现在想想可能就是被这些概念吓到了当时,等你仔细的弄懂了它们是什么意思,理解起来难度就会小很多啦,所以,我决定先从概念开始说起,捋顺一下思路,至于条件随机场先表过不谈!
我们先来看一下整个大框架下,条件随机场在什么位置,让读者心中有数,知道自己到底在学什么,如图:
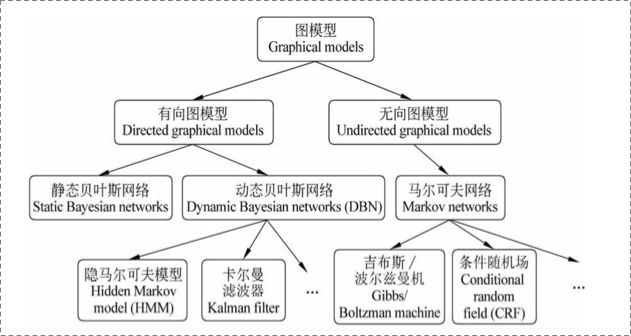
可以看出 在图模型这个大框架下分成了两类:
1有向图模型 有向图模型又分为:静态贝叶斯网络 和动态贝叶斯网络 动态贝叶斯网络再具体细分就是 隐马尔科夫模型 和 卡尔曼滤波器
2 无向图模型 分为马尔科夫网络 马尔科夫网络分成 吉布斯/波尔兹曼机和 条件随机场
所谓的有向图模型一般用于对日常生活中的一些有着明显依赖关系,因果关系的问题进行建模,而无向图模型则是用于给日常生活中那些具有相互依赖关系的问题进行建模!
这里我可以贴一下上一篇HMM画的图给大家感受一下这个区别:
有向图模型(以隐马尔科夫模型举例): 无向图模型(以马尔科夫网络举例):

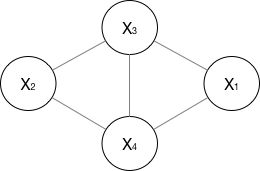
这里着重的看有向图和无向图两种概念的直观区别,一个是单项依赖关系 另一个是相互依赖关系!
下面正式开始本篇博客的内容讲解:
1准备部分:
主要是进行概念的梳理和理解:
1 图: 图是由结点和连接结点的变组成的集合,结点和边分别记作v和e,结点和边的集合分别记作V和E,图记作G=(V,E) 不难理解
2 随机场:所谓的随机场就是指一组样本空间相同的随机变量的集合,而且一般情况下随机变量之间存在依赖关系,否则没有什么意义
3 马尔科夫独立性假设: 马尔科夫独立性假设是说,对于一个节点,在给定它所连接的所有节点的前提下,它和外界是独立的,也就是说如果观测到一个节点的取值是常量,那么别的节点就无法通过它来进一步影响其他的节点,所以,如果我们给定了与一个节点连接的所有的节点,那么这个节点就和外界相互独立了!
4 马尔科夫随机场: 下面进行一个概念的组合: 2+3=? 随机场+马尔科夫独立性假说=马尔科夫随机场!没错,所谓的的马尔科夫随机场,就是遵循着马尔科夫独立性假说的随机场!
5 概率无向图模型: 设有联合概率分布P(Y),由无向图G=(V,E)表示,在图G中,结点表示随机变量,边表示随机变量之间的依赖关系,如果联合概率分布P(Y)满足成对马尔科夫性,局部马尔科夫性,全局马尔科夫性,
那么就称此联合概率分布为概率无向图模型或者马尔科夫随机场!
这个概念一敲出来可能会有一小部分童鞋有点糊涂,什么是局部马尔科夫性,什么是成对马尔科夫性,什么是全局马尔科夫性呢?其实三者是等价的,这里只介绍一种 全局马尔科夫性,先上图
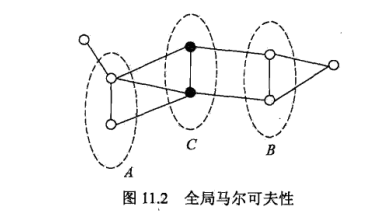
6 全局马尔科夫性:设结点集合A,B是在无向图G中被结点集合C分开的任意结点集合,如图11.2,结点集合A,B,C对应的随机变量组分别是,全局马尔科夫性指的是在给定随机变量
的条件下随机变量
是条件独立的!用公式表示就是:
写到这里可能大家就清楚了,之所以概率无向图模型=马尔科夫随机场,就是因为定义时候所谓的马尔科夫独立性假设和这里的全局马尔科夫性,局部马尔科夫性,成对马尔科夫性本质上讲的都是一个东西啊!
写了这么多,怎么还不开始说条件随机场啊!这是要急死人的节奏啊,嘿嘿不着急,容我再讲一个定义!
其实概率无向图有一个很好的性质就是它可以进行因式分解,对!因式分解!想了解因式分解,必须要先解锁 团和最大团的概念!
附加: 1 团和最大团: 无向图G中任何两个结点均有边连接的结点子集称之为团!若C是无向图G中的一个团,并且不能再加进任何一个G的结点使其成为一个更大的团,则称此C为最大团!
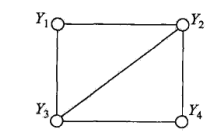
如图所示:2结点组成的团有 {Y1,Y3}, {Y1,Y2}, {Y2,Y3}, {Y3,Y4}, {Y2,Y4} 有两个最大团:{Y1,Y2,Y3},{Y2,Y3,Y4},之所以{Y1,Y2,Y3,Y4}不能成为一个最大团是因为Y1,Y4之间没有边连接!
下面正式开始概率无向图模型的因式分解:将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因式分解!太形式化的概念文就不给了
直接给公式看得很清楚:
,而Z是其规范化因子,由式:
决定,
通俗点解释就是,P(Y)这个联合概率可以分解成最大团上的函数的乘积的形式,而要真正的形成概率,必须用规范化因子Z进行相除!
2 正式介绍部分:
有了上述充足的准备,就正式进入条件随机场的介绍了,直接给出条件随机场的定义!
条件随机场: 设X与Y是随机变量,P(Y|X)是在给定X的条件下Y的条件概率分布,若随机变量Y构成一个由无向图G=(V,E)表示的马尔科夫随机场,即:
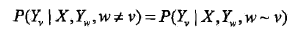 对任意的结点v成立,则称条件概率分布P(Y|X)为条件随机场
对任意的结点v成立,则称条件概率分布P(Y|X)为条件随机场
这个概念看起来挺抽象的涉及到了很多其他的概念,此时如果你回去再看一遍开头我们的定义部分,就会明白许多,所谓的条件随机场不过是一组随机变量X,Y形成的条件概率的集合,但是这个条件概率满足了马尔科夫独立性假设/概率无向图模型的条件,所以我们称之为条件随机场! 上述公式的解释也很直观,那就是:所有不跟我直接相连的变量都跟我没关系!
如果不理解的童鞋,那只能反复的读概念,反复的捋顺了~
条件随机场我们是了解了,但是我们能用它来做啥呢?我们都知道,从概率无向图模型的角度去想,一些相互依赖的随机变量构成的图模型,好像有点复杂对不对,是啊,错综复杂的相互依赖关系,
对应的肯定是一个无比复杂的联合概率分布模型,那我们就解释一个特殊情况吧!线性模型应该是最简单的了吧!那就将概率图模型简化成线性!没错,知难而退!线性链条件随机场,叫你呢,快去报道!
线性链条件随机场: 设 均为线性链表示的随机变量序列,若在给定随机变量序列的X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔科夫性:
均为线性链表示的随机变量序列,若在给定随机变量序列的X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔科夫性:
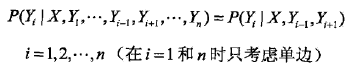
那么我们就称P(Y|X)为线性链条件随机场! 这个概念也不难理解,就是在条件随机场的基础之上,固定了无向图的结构,没错,我就是强制你只能玩最简单的线性就得了!这就是线性链条件随机场本人了!
放张图各位了解一下:
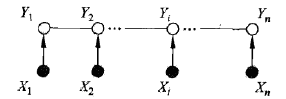 (线性链条件随机场)
(线性链条件随机场)
一大堆空洞的概念敲完,全都是在定性的说事,并没有定量的讲到底是什么,连最大团上的函数的具体形式都没有给出,下面干货来了,线性链条件随机场的参数化形式:
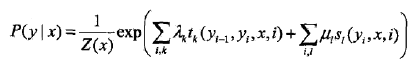
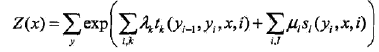
这两个公式放出来,可能各位老哥们要关掉这篇博文了,你妹的,你讲了些什么啊,就放几个难懂的公式?别着急,下面开始解释一哈:
之前我们说过,概率无向图(马尔科夫随机场)可以进行因式分解,并且给出因式分解的定性的表达式:
各位一定还记得吧! 求求你们一定要记得!这个在最大团上定义的函数称之为势函数,而且这个势函数必须是严格正的,通常情况下定义为指数函数:
求求你们一定要记得!这个在最大团上定义的函数称之为势函数,而且这个势函数必须是严格正的,通常情况下定义为指数函数:

没错,第一个式子分子一大堆就是最大团上的势函数!exp保证了势函数的严格正的性质,而里面的东西是啥呢?
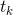 是定义在边上的特征函数,称为转移特征,依赖于当前和前一个位置!如果满足条件那就为1,如果不满足就为0,你可能会想,特征函数听起来这么牛逼,难道就是个二值函数吗?
是定义在边上的特征函数,称为转移特征,依赖于当前和前一个位置!如果满足条件那就为1,如果不满足就为0,你可能会想,特征函数听起来这么牛逼,难道就是个二值函数吗?
没错就是这么任性,别忘了特征有很多个啊!随便你定义多少个特征,而且这个特征的定义往往是要根据具体的情况具体确定的,打个总结!(现在你晓得我叫王闪火,重要的事我从来都不闪躲!)跑飞了。。。
举个例子!!那就是比如我前面一个词是阶词,后一个词是名词,如果满足这个条件,那我就让特征函数为1,然后用这个特征函数去扫描整个句子,满足条件的不就出来了嘛!最后这个特征函数会给这个句子打分
拍子不稳啊!skr~ Fail,然后把许多特征函数的得分加起来就是这个句子的总得分,再处以归一化因子,就得到了这个标注的真正的概率!
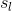 也是一样,不过它是定义在结点上的函数,称之为状态特征,依赖于当前的位置,也是根据具体的规则满足就call 1 不满足就call 0
也是一样,不过它是定义在结点上的函数,称之为状态特征,依赖于当前的位置,也是根据具体的规则满足就call 1 不满足就call 0
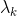 ,
,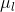 分别是转移特征和状态特征对应的权值!你打分怎样也会有个重要性话语权吧,这两个变量就是话语权,它们和特征函数联合起来唯一确定了一个条件随机场!
分别是转移特征和状态特征对应的权值!你打分怎样也会有个重要性话语权吧,这两个变量就是话语权,它们和特征函数联合起来唯一确定了一个条件随机场!
如果讲到这里你还是不理解,那你就想中国新说唱就是一个势函数,wuli凡凡就是专门研究flow和hook的衔接的,如果过渡的很好,就给他pass对应1,如果拍子不稳,那就给fail对应0
相应的热狗和张震岳这么有水平肯定看beats,听break和节奏,对应着状态特征啊!如果好就pass,不好就fail ,潘帅和邓紫琪负责歌词部分,也给选手打分,那三组制作人肯定打分要有个
权重啊,wuli凡凡肯定是C咖大神,我觉得比重0.5,狗哥和潘帅组一个0.2 一个0.3吧,这样总分就出来了,归一化就把所有选手得分加起来,然后用本选手的得分去除!差不多是这个意思ba~
我觉得我已经讲的很清楚了!贴一个李航老师《统计学习方法》中的例子给大家加深一下印象:

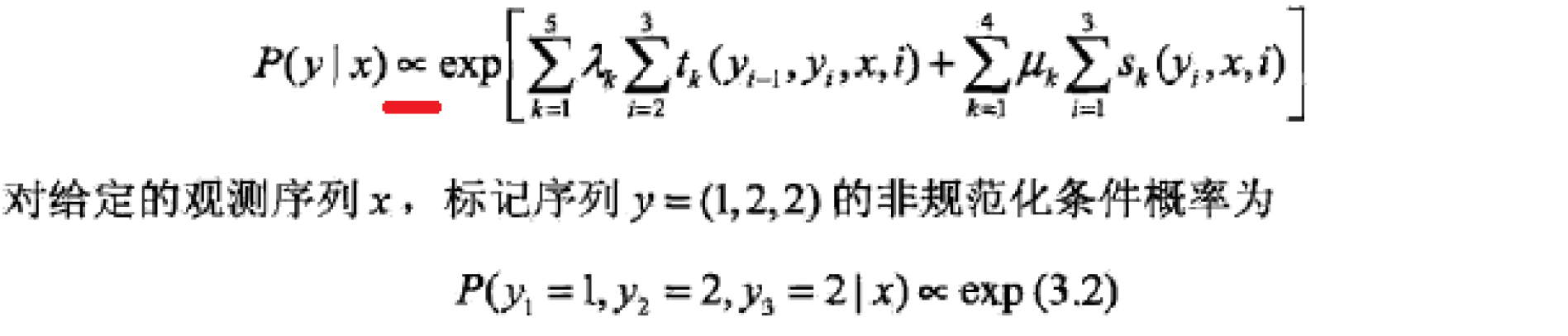
条件随机场的简化形式这里就不说了,其实就是将转移特征和状态特征进行排列,形成一个统一的特征函数的规范,同样将权值进行排列,然后将写成两个向量相乘的形式,没有什么本质上的变化,不过是形式上更好看了而已。
重点描述一下条件随机场的矩阵形式,因为这部分内容我当时在看书的时候十分的困惑,有许多不懂的地方,这里将我的思路贴出来给大家参考,可能对看不懂书的同学更有帮助一点吧!
矩阵形式:
条件随机场还可以由矩阵形式表示,假设是线性链条件随机场,表示对给定观测序列x,相应的标记序列y的条件概率,引进特殊的起点和终点状态标记
,这时,
可以通过矩阵的形式表示,对观测序列x的每一个位置i=1,2.......n+1,定义一个m阶矩阵(m是标记yi取值的个数)
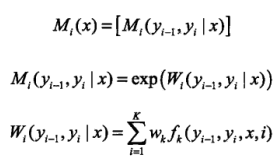
这样,给定观测序列x,标记序列y的非规范化概率可以通过n+1个矩阵的乘积表示,于是,条件概率是:

针对条件随机场的矩阵形式,这里要解释几点:
1矩阵的阶数为mxm阶,因为对于i-1状态可以选的取值yi-1有m种,同样变换到yi可选的取值也会有m种,这样便形成了mxm的矩阵
2 矩阵中每一个元素其实是从i-1到i状态的非规范化概率,直到我写这篇博客的时候我还在思考,矩阵形式的定义里第三个式子,下标应该
是写错了,我认为应该是对k求和才是正确的,千万不要对i求和,因为它就是表示的从i-1---->i这两个状态的非规范化概率,如果你对i求和那就全乱套了,第三个式子的意思就是将i-1----->i的所有的特征函数(包含转移特征和状态特征)加权求和,然后再exp一下保证非负,形成所谓的非规范化概率!
3 基于2的解释,我们可以了解到Mi(x)其实就相当于HMM中我们所熟知的状态转移概率,从上一个状态转移到下一个状态!类比着理解一下
4 前面反复的强调非规范化概率,那么规范化因子该如何求解呢?事实上,是M1(x)M2(x)M3(x)......Mn+1(x)的矩阵相乘形成的矩阵的第start行第stop列的元素就是我们的规范化因子其代表了从start到stop的所有可能的路径的非规范化概率之和?那为啥矩阵的第start行第stop列就是所有可能路径的非规范化概率之和呢?我相信答案我已经在前面的解释给出了,
动动脑筋思考一下ba~
5最后要解释的是 这里的start和stop并不是什么神秘的东西,它可以是1.2.3.4......m的任意值,根据你的观测序列或者实际情况确定的!
介绍完了条件随机场,同样贴一个例子来验证一下上述结论是否正确~:


好了,写到这里,条件随机场的基本知识你已经弄懂了,下面的文章会和HMM一样分成1概率计算 2学习问题 3预测问题三部分 而我的这篇博客会重点写一下概率计算问题,因为涉及到前向后向的公式理解
而学习问题就是对条件概率进行极大似然估计,然后用拟牛顿法和改进迭代尺度法进行优化,求出参数向量w,学习问题就不讲了,因为本身拟牛顿法和改进的迭代尺度算法不是我擅长的部分,各位有好的资料可以
共享一下,至于预测算法,就是利用维特比算法进行概率最大化的译码过程,这个在信息论与编码里面学过,后面我会专门写一篇维特比译码算法的博文,到时候可以关注一下!
接下来的重点就是概率的计算问题:
其实概率的计算问题可以类比着HMM去理解,因为里面很多的思想都是相通的,前向后向概率之类的概念
之前我们说过,矩阵形式中每一个矩阵元素代表着从i-1状态到i状态的非规范化概率,对于每一个指标i=0,1,.....n+1,定义前向向量和递推公式:
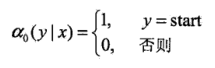

也可以表示为: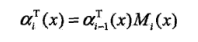
表示在位置i的标记是yi并且到位置i的前部分标记序列的非规范化概率,这样再乘上矩阵中的元素
就可以顺利的从一个状态递推到下一状态,并且乘积仍然是非规范化概率
yi的取值可以是m个,所以是m维的向量!
......
......
......
这个地方参考李航统计学习方法,后续更新,重点写书上没有的内容
独立思考部分:
这部分讲两个问题 一: 条件随机场和隐马尔科夫模型的关系到底是什么?
二: 条件随机场和logistic模型的关系又是什么?
一:条件随机场和隐马尔科夫模型的关系
这个问题的解答是看了网上一篇博客,看完之后有一种顿悟的感觉,整理在这里,争取让这篇博客成为最强条件随机场参考资料,哈哈!(文末附上链接)
其实条件随机场主要的应用方向还是NLP 具体点应用在词性标注方面比较多,所以这里就举词性标注的例子,那么首先我们回想一下,如果是HMM模型,在已知句子s的前提下如何进行词性标注呢?这应该就是HMM模型下的已知HMM模型及其参数,已知观测序列,让你求出生成观测序列的概率,对应着概率的计算问题!那么,用最便于理解的暴力求解方法,公式如下:
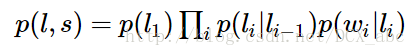
是初始状态概率,
是状态转移概率
是对应着发射概率!然后对所有可能的状态i求和生成的就是产生观测s的概率!这是HMM告诉我们的通常的解法!那么它和CRF条件随机场有什么关系呢?
结论是条件随机场要比HMM强大的多,HMM的模型限制了它的性能,后面我们会具体的解释这个问题,事实上,如果我们对暴力求解的方法上式取对数,模型就变成:
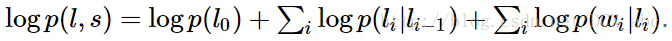
然后我们再考虑一下我们的条件随机场的公式:
如果我们不取势函数为exp,而是在特征函数的定义过程中直接保证其非负性(特征函数可以人为进行规定),那么其非规范化概率可以写为:
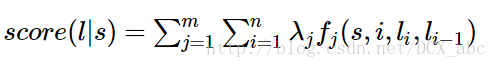
仔细比较上下两式,其实结果都是一样的 特征函数在整个句子上扫描打分的结果值再针对所有的特征函数求和!本质上是一个公式!
接下来我们再比较一下条件随机场和隐马尔科夫模型针对相同问题的公式的形式:
HMM: 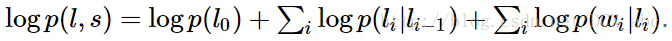
CRF: 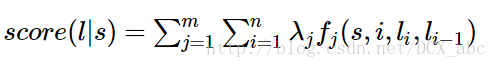
可以看出,如果将HMM的log形式的概率看作是转移特征函数的分数的权值tk,而将
看作是状态特征函数的权值λi,那么HMM的式子和CRF的式子其实就是具有相同的形式,或者不严谨的说,二者是一样的!
可能有同学会问,照你这个思路为什么HMM只有权值求和后面却没有特征函数呢?因为相加求和只有特征函数为1的才会保留下来,别忘了特征函数实际上是二值函数(0-1)相加起来实际上是只有权值在相加,因为特征函数等于1!
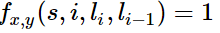 这样!
这样!
也就是说,我们可以用这个思路来构建一个CRF,让它和HMM的几乎完全相同!如何构造呢?
就是沿着刚才的思路反向思考,针对每一个HMM,它的每一个转移概率我都定义一个特征函数与之对应,而且当且仅当li-1=x,li=y的时候,我才规定这个特征函数的值为1
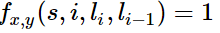 ,而且此特征函数对应的权值我就让它等于转移概率的对数概率:
,而且此特征函数对应的权值我就让它等于转移概率的对数概率:,后面的状态概率也是同样的定义方式,用这样的定义方式得到的关于词性标注问题的HMM方法和CRF方法的结果几乎是一模一样,作为这个模型的创造者,我们自然知道原因,毕竟二者本质上其实是一样的哈哈!
因此,每一个HMM都有一个CRF与之对应!
所以我们可以解释之前说的为什么HMM的模型其实限制了HMM的性能,观察用CRF构造HMM的方法我们可以发现:
1因为HMM定义时,规定当前状态的变化只和前一个状态有关系,所以定义特征函数时候,只能够定义和相邻状态有关的特征函数,而CRF就没有这个限制了,它允许你从整个句子的角度去考虑全局特征,你甚至可以定义句子开头和结尾的两个状态之间的关系,这大大增加了CRF的定义特征的能力!这种能力是CRF望尘莫及的!
2从CRF与HMM的对应我们同样可以发现,HMM的特征函数的取值是对数概率,也就是说它必须取负值,也只能取负值!而且既然是概率那么它一定要满足概率完备性条件才可以,但是CRF的权值你是可以随意操作的!
3最重要的一点就是:HMM本质上是基于贝叶斯网络(从属于有向图)的生成模型,模型从联合概率的角度考虑,而我们的CRF是一种判别式模型,直接寻找判决边界,从条件概率的角度去考虑!
二:条件随机场和logistic模型之间的关系:
其实我们从条件随机场的定义中可以发现,二者都是属于对数线性模型!(虽然我对对数线性模型当中的线性没有考虑到什么直观的解释,如果对于多项式的话),也就说二者在结构上使用的是一种模型:
条件随机场:
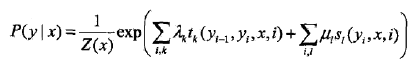
logistic回归模型:
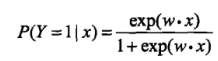 (二项logistic回归,其分母其实也是一个规范化因子Z)
(二项logistic回归,其分母其实也是一个规范化因子Z)
从二者的公式我们可以看出,本质上二者果然都是对数线性模型,不过是exp括号里面的内容不一样,logistic在括号里面直接给出的是一个线性函数,用来进行对平面的划分,而条件随机场的exp括号里是对所有特征函数对整个句子的打分情况求和,描述的是整个句子序列的结点关系和状态转移的关系,二者最后都形成了一个真正的概率值,所以说,条件随机场其实就是序列化的logistic模型,你同意这个观点吗?或者你有更好的解释,欢迎在下面给我留言,相互交流,我能想到的就只有这些啦!
向各位读到最后的读者致谢,希望你们看完博客能够有所收获!同时也向文末的博客的博主致谢,感谢你翻译并解释这么棒的条件随机场资料给大家,Thanks!
参考博客:
如何轻松愉快的了解条件随机场?https://www.jianshu.com/p/55755fc649b1

