非线性支持向量机基础——核函数之我见
写在前面,核函数方法不一定非得用在支持向量机上,任何只要出现内积<Xi,Xj>或者说你在求解线性问题,而权重w恰好是训练样本的加权组合的情况下,都可以用上核函数的方法,来做到提升维度,进而完成非线性到线性转换的一个目的。
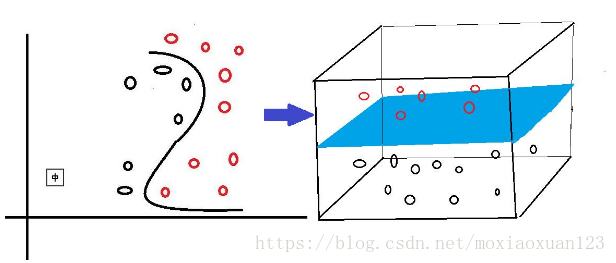
可能有同学不理解,为什么从低维度升到高纬度就能够做到从原本线性不可分的情况一下子变成了线性可分了呢,我举一个吃货们最能体会的例子,你用面团做一个花卷,你把面揉成面饼,然后拉成一个平面,在平面上半部分撒上沙子,下半部分撒上芝麻,然后你弯曲一下搞成个S型,捏住上端提起来,用如来神掌一压,请问这时候你还下得去嘴吗,沙子你敢吃吗?嘎嘣脆啊哈哈哈哈,但是仔细想一想,你搞成像带鱼一样S型的时候,如果此时,你沿着芝麻和沙子的分界线还是很容易一刀切下去,从而将含沙子的面和含芝麻的面分开的不是吗? 其实你从上帝视角压扁之后,相当于做了维度的压缩,在二维平面上,根本无法区分开沙子和芝麻,但是你提成s型的曲面,多了一个高度的维度,此时低维上升到了高维,区分起来就十分容易了,是不是很有画面感?
上一张图感受一下:(原谅我实在是不会画图,图是百度图库copy下来的,后续会更上自己的图)
讲完了思想再来正式的介绍一下本篇文章的主角,核函数,这里还是引用《统计学习方法》李航老师的定义:
核函数:设X是输入空间(欧式空间的子集或离散集合),又设
为特征空间(希尔伯特空间),如果存在一个X到H的映射:
使得对于所有的
,函数
满足条件:
则称为核函数,
为映射函数,式中
为两个映射函数的内积。
通常我们在使用核函数的时候,可以不必显式的指定对应的映射函数,因为映射函数通常都是从输入空间到特征空间的一个映射,而为了达到我们的目的,这通常都是一个升维的过程,特征空间的维度往往比较大,甚至无穷维度(RBF),所以,我们只需要指定核函数就可以,而不必要显式指定映射函数,这里提一点,映射后特征空间和对应的映射函数不唯一,就算是同一个特征空间对应的映射函数也不唯一。
介绍完了核函数,回到我们的支持向量机的主题上来,上篇博文中讲到,应用拉格朗日对偶,最终可以将线性支持向量机转化为以下的最优化问题:
注意到括号里面的内容,是两个数据样本的内积,如果此时我们将内积用我们的核函数来取代,那么对应的目标函数就可以变成:
将训练样本的内积转化为核函数有什么意义呢? 其实训练样本级别的内积相当于在输入空间进行的操作,而转换成对应的核函数,相当于完成了两个映射函数的内积,进一步讲是完成了两个高维特征空间的内积,这样带给我们最直接的好处就是,如果映射函数是非线性函数,那么我们在特征空间学习到的SVM(支持向量机)其实就已经具备非线性的分类能力。
可能又有同学会问了,兄弟,你不是说了映射函数不需要显式的给出吗,怎么又在大谈映射函数的非线性呢?
其实,李航老师的书本里说过了,在实际应用中,往往根据领域的知识直接选择核函数,也就是你选择核函数的时候就已经知道了其对应的映射函数是否非线性,进而知道你这样做出来的支持向量机是否具备非线性分类能力,下面介绍几个常用的核函数:
1 多项式核函数(polynomial kernel funciton):
2 高斯核函数(Gaussian kernel fuction):
这个函数就厉害啦,因为其长得和高斯函数相像而得名,也叫径向基函数,它对应的支持向量机为高斯径向基函数分类器,也就是我们熟知的RBF,前面提到的映射函数映射之后有无穷的维度指的就是这个函数,具体为什么映射之后有无穷维,这里截图一下李宏毅老师的机器学习课件给大家看,就是一个泰勒公式的展开:
最后一个部分我们来阐述一下一个函数可以称作是核函数的一个充要条件:
给定一个函数,那么这个函数是核函数的充要条件是什么呢?
对于一个训练样本 ,我们任取一个变量
和
,将它带入到函数中
,因为训练样本共有n个,那么一共会有n*n个元素,将这n*n个元素组成一个矩阵,我们称之为核函数矩阵(kernel matrix)
根据核函数的定义我们有:
可见,如果这个函数是核函数那么它对应的核函数矩阵一定是一个对称阵!这是一个很好的性质,
对于任意的向量n,我们有:
![clip_image078[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034522383.png)
也就是说如果函数K是一个有效的核函数,那么其对应的核函数矩阵其实是半正定的!(必要条件)
同时,这个结论的充分性也是满足的,由Mercer定理给出,这样我们就得到了一个函数能否作为核函数的一个充要条件!