[C2W3] Improving Deep Neural Networks : Hyperparameter tuning, Batch Normalization and Programming Frameworks

第三周：Hyperparameter tuning, Batch Normalization and Programming Frameworks

调试处理（Tuning process）

目前为止，你已经了解到，神经网络的改变会涉及到许多不同超参数的设置。现在，对于超参数而言，你要如何找到一套好的设定呢？在本节中，我想和你分享一些指导原则，一些关于如何系统地组织超参调试过程的技巧，希望这些能够让你更有效的聚焦到合适的超参设定中。

关于训练深度神经网络最难的事情之一是你要处理的参数的数量，下面粗略了解下哪些超参数较为重要：

• \(\alpha\) 学习速率是需要调试的最重要的超参数。

接下来：

• hidden units，调试隐藏单元数量

• mini-batch size，调试 mini-batch 大小以确保最优算法运行有效

比较次要的：

• layers，调试网络层数

• learning rate decay，学习率衰减

还有一些固定的：

• 应用 Momentum 和 Adam 优化算法时的超参数 \(\beta = 0.9\)，\(\beta_{1} = 0.9\)，\({\beta}_{2} = 0.999\) 和 \(\varepsilon = 10^{-8}\)

如果你尝试调整一些超参数，该如何选择调试值呢？

在早一代的机器学习算法中，如果你有两个超参数，这里我会称之为超参 1，超参 2，常见的做法是在网格中取样点，如上图，然后系统的研究这些数值。这里我放置的是 5 × 5 的网格，实践证明，网格可多可少，但对于这个例子，你可以尝试这所有的 25 个点，然后选择哪个参数效果最好。当参数的数量相对较少时，这个方法很实用。

在深度学习领域，我推荐你采用随机选择点的方法，如上图，你同样可以选择同等数量的 25 个点，接着，用这些随机取的点试验超参数的效果。之所以这么做是因为，对于你要解决的问题而言，你可能很难提前知道哪个超参数最重要，但事实是，正如你之前看到的，确实会有一些超参数要比其它的更重要。

举个例子，假设超参数 1 是 \(\alpha\)（学习速率），取一个极端的例子，假设超参数 2 是 Adam 算法中的分母中的 \(\varepsilon\)。在这种情况下，\(\alpha\) 的取值很重要，而 \(\varepsilon\) 取值则无关紧要。但假设我们提前不知道 \(\alpha\) 和 \(\varepsilon\) 的重要性，现在如果你在网格中取点，接着，你试验了 \(\alpha\) 的 5 个取值，那你会发现，无论 \(\varepsilon\) 取何值，结果基本上都是一样的。所以，虽然你有 25 种模型，但进行试验的 \(\alpha\) 值只有 5 个，这不是高效率的。对比而言，如果你随机取值，你就会试验 25 个独立的 \(\alpha\)，似乎你更有可能发现效果做好的那个。

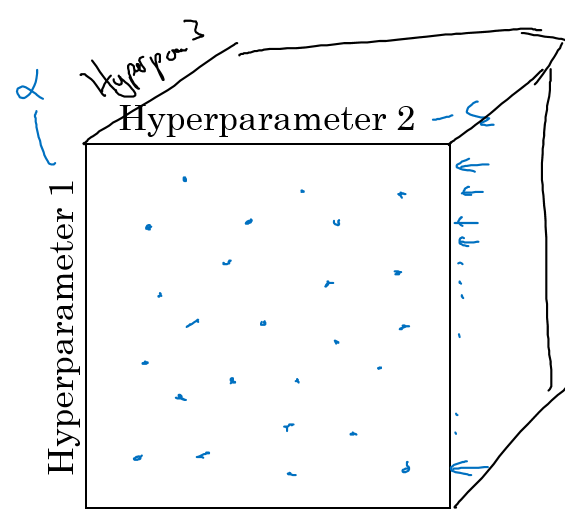
上面解释了两个超参数的情况，实践中，你搜索的超参数可能不止两个。假如，你有三个超参数，这时你搜索的不是一个方格，而是一个立方体，如上图所示，超参数 3 代表第三维，接着，在三维立方体中取值，你会试验大量的更多的值。实践中，你搜索的可能不止三个超参数。有时很难预知，哪个是最重要的超参数，对于你的具体应用而言，随机取值，而不是网格取值，这表明你探究了更多重要超参数的潜在值，无论结果是什么。

当你给超参数取值时，另一个惯例是采用由粗糙到精细的策略。（Coarse to fine）

如上图，比如在上面那个例子中，你进行了取值，然后你发现了效果最好的某个点，也许这个点周围的其他一些点效果也很好，那在接下来要做的是放大这块小区域（小蓝色方框内），然后在其中更密集得取值或随机取值，聚集更多的资源，在这个蓝色的方格中进行粗略的搜索后，你会知道接下来应该聚焦到更小的方格中。在更小的方格中，你可以更密集得取点。所以这种从粗到细的搜索也经常使用。

通过试验超参数的不同取值，你可以选择对训练集目标而言的最优值，或对于开发集而言的最优值，或在超参搜索过程中你最想优化的东西。

希望这能给你提供一种方法去系统地组织超参数搜索过程，其中的关键点是 随机取值 和 精确搜索，但超参数的搜索内容还不止这些，在下一节中，我会继续讲解关于如何选择超参数取值的合理范围。

为超参数选择和适合范围（Using an appropriate scale to pick hyperparameters）

在上一节中，你已经看到了在超参数范围中，随机取值可以提升你的搜索效率。但随机取值并不是在有效范围内的随机均匀取值，而是选择合适的标尺，用于探究这些超参数，这很重要。在本节课中，我会教你怎么做。

假设你要选取隐藏单元的数量 \(n^{[l]}\)，假设，你选取的取值范围是从 50 到 100 中某点，这种情况下，都是正整数，你可以随机在 50 - 100 范围内取点，这是一个搜索特定超参数的很直观的方式。或者，如果你要选取神经网络的层数，也是一样，我们称之为字母 \(L\)，你也许会选择层数为 2 到 4 中的某个值，然后顺着 2，3，4 随机均匀取样，然后你还可以将其应用到网格搜索，这是在几个在你考虑范围内随机均匀取值的例子，或许你也发现了，这些都是一些离散值，这些取值还蛮合理的，但对某些超参数而言却不适用。

再看一个例子，假设你在搜索超参数 \(\alpha\)（学习速率），假设你怀疑其值最小是 0.0001 或最大是 1。如果你画一条从 0.0001 到 1 的数轴，沿其随机均匀取值，那 90% 的数值将会落在 0.1 到 1 之间，结果就是，在 0.1 到 1 之间，应用了 90% 的资源，而在 0.0001 到 0.1 之间，只有 10% 的搜索资源，这看上去不太对。

但是如果你用对数标尺搜索超参数的方式则会更合理，分别依次取 0.0001，0.001，0.01，0.1，1 为刻度，在对数轴上均匀随机取点，这样，在 0.0001 到 0.001 之间，就会有更多的搜索资源可用，还有在 0.001 到 0.01 之间也同样，以及其他区间也是如此等等。

所以在 Python 中，你可以这样做，使

r = -4 * np.random.rand()
\(\alpha = 10^{r}\)

所以，第一行可以得出 \(r \in [-4, 0]\)，那么 \(\alpha \in [10^{-4},10^{0}]\)，所以最左边的数字是 \(10^{-4}\)，最右边是 \(10^{0}\)。

更常见的情况是，如果你在 \(10^{a}\) 和 \(10^{b}\) 之间取值，在此例中，这是 \(10^{a}\)（0.0001），你可以通过 \(\operatorname{}{0.0001}\) 算出 \(a\) 的值，即 -4，在右边的值是 \(10^{b} = 1\)，你可以算出 \(b\) 的值，即 0。你要做的就是在 \([a,b]\) 区间随机均匀地给 \(r\) 取值，这个例子中 \(r \in \lbrack - 4,0\rbrack\)，然后你可以设置 \(a\) 的值，基于随机取样的超参数 \(\alpha =10^{r}\)。

所以总结一下，在对数坐标下取值，取最小值的对数就得到 \(a\) 的值，取最大值的对数就得到 \(b\) 值，所以现在你在对数轴上的 \(10^{a}\) 到 \(10^{b}\) 区间取值，在 \(a\)，\(b\) 间随意均匀的选取 \(r\) 值，将超参数设置为 \(10^{r}\)，这就是在对数轴上取值的过程。

最后，另一个棘手的例子是给 \(\beta\) 取值，用于计算指数的加权平均值。假设你认为 \(\beta\) 是 0.9 到 0.999 之间的某个值，也许这就是你想搜索的范围。记住这一点，当计算指数的加权平均值时，取 0.9 就像在 10 个值中计算平均值，有点类似于计算 10 天的温度平均值，而取 0.999 就是在 1000 个值中取平均。

所以和上张幻灯片上的内容类似，如果你想在 0.9 到 0.999 区间搜索，那就不能用线性轴取值，对吧？不要随机均匀在此区间取值，所以考虑这个问题最好的方法就是，我们要探究的是 \(1-\beta\)，此值在 0.1 到 0.001 区间内，所以我们会给 \(1-\beta\) 取值，大概是从 0.1 到 0.001，应用之前幻灯片中介绍的方法，这是 \(10^{-1}\)，这是 \(10^{-3}\)，值得注意的是，在之前的幻灯片里，我们把最小值写在左边，最大值写在右边，但在这里，我们颠倒了大小。这里，左边的是最大值，右边的是最小值。所以你要做的就是在 \([-3,-1]\) 里随机均匀的给r取值。你设定了 \(1- \beta = 10^{r}\)，所以 \(\beta = 1-10^{r}\)，然后这就变成了在特定的选择范围内超参数随机取值。希望用这种方式得到想要的结果，你在 0.9 到 0.99 区间探究的资源，和在 0.99 到 0.999 区间探究的一样多。

所以，如果你想研究更多正式的数学证明，关于为什么我们要这样做，为什么用线性轴取值不是个好办法，这是因为当 \(\beta\) 接近 1 时，所得结果的灵敏度会变化，即使 \(\beta\) 有微小的变化。所以 \(\beta\) 在 0.9 到 0.9005 之间取值，无关紧要，你的结果几乎不会变化。

但 \(\beta\) 值如果在 0.999 到 0.9995 之间，这会对你的算法产生巨大影响，对吧？在这两种情况下，是根据大概 10 个值取平均。但这里，它是指数的加权平均值，基于 1000 个值，现在是 2000 个值，因为这个公式 \(\frac{1}{1- \beta}\)，当 \(\beta\) 接近 1 时，\(\beta\) 就会对细微的变化变得很敏感。所以整个取值过程中，你需要更加密集地取值，在 \(\beta\) 接近 1 的区间内，或者说，当 \(1-\beta\) 接近于 0 时，这样，你就可以更加有效的分布取样点，更有效率的探究可能的结果。

希望能帮助你选择合适的标尺，来给超参数取值。如果你没有在超参数选择中作出正确的标尺决定，别担心，即使你在均匀的标尺上取值，如果数值总量较多的话，你也会得到还不错的结果，尤其是应用从粗到细的搜索方法，在之后的迭代中，你还是会聚焦到有用的超参数取值范围上。

希望这会对你的超参数搜索有帮助，下一节中，我们将会分享一些关于如何组建搜索过程的思考，希望它能使你的工作更高效。

超参数训练的实践：Pandas vs. Caviar（Hyperparameters tuning in practice: Pandas vs. Caviar）

到现在为止，你已经听了许多关于如何搜索最优超参数的内容，在结束我们关于超参数搜索的讨论之前，我想最后和你分享一些建议和技巧，关于如何组织你的超参数搜索过程。

如今的深度学习已经应用到许多不同的领域，某个应用领域的超参数设定，有可能通用于另一领域，不同的应用领域出现相互交融。比如，我曾经看到过计算机视觉领域中涌现的巧妙方法，比如说 Confonets 或 ResNets，这我们会在后续课程中讲到。它还成功应用于语音识别，我还看到过最初起源于语音识别的想法成功应用于NLP等等。

深度学习领域中，发展很好的一点是，不同应用领域的人们会阅读越来越多其它研究领域的文章，跨领域去寻找灵感。

就超参数的设定而言，我见到过有些直觉想法变得很缺乏新意，所以，即使你只研究一个问题，比如说逻辑学，你也许已经找到一组很好的参数设置，并继续发展算法，或许在几个月的过程中，观察到你的数据会逐渐改变，或也许只是在你的数据中心更新了服务器，正因为有了这些变化，你原来的超参数的设定不再好用，所以我建议，或许你需要重新测试或评估你的超参数，至少每隔几个月一次，以确保你对数值依然很满意。

最后，关于如何搜索超参数的问题，我见过大概两种重要的思想流派或人们通常采用的两种重要但不同的方式。

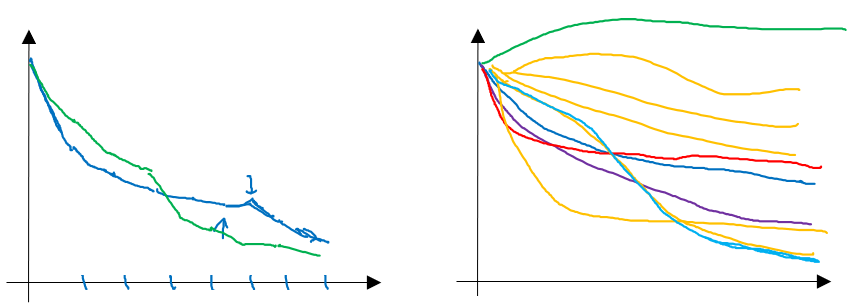
（上左图）一种是你照看一个模型，通常是有庞大的数据组，但没有许多计算资源或足够的 CPU 和 GPU 的前提下，基本而言，你只可以一次负担起试验一个模型或一小批模型，在这种情况下，即使当它在试验时，你也可以逐渐改良。比如，第 0 天，你将随机参数初始化，然后开始试验，然后你逐渐观察自己的学习曲线，也许是损失函数 \(J\)，或者数据设置误差或其它的东西，在第 1 天内逐渐减少，那这一天末的时候，你可能会说，看，它学习得真不错。我试着增加一点学习速率，看看它会怎样，也许结果证明它做得更好，那是你第二天的表现。两天后，你会说，它依旧做得不错，也许我现在可以填充下 Momentum 或减少变量。然后进入第三天，每天，你都会观察它，不断调整你的参数。也许有一天，你会发现你的学习率太大了，所以你可能又回归之前的模型，像这样，但你可以说是在每天花时间照看此模型，即使是它在许多天或许多星期的试验过程中。所以这是一个人们照料一个模型的方法，观察它的表现，耐心地调试学习率，但那通常是因为你没有足够的计算能力，不能在同一时间试验大量模型时才采取的办法。

（上右图）另一种方法则是同时试验多种模型，你设置了一些超参数，尽管让它自己运行，或者是一天甚至多天，然后你会获得像这样的学习曲线，这可以是损失函数J或实验误差或损失或数据误差的损失，但都是你曲线轨迹的度量。同时你可以开始一个有着不同超参数设定的不同模型，所以，你的第二个模型会生成一个不同的学习曲线，也许是像这样的一条（紫色曲线），我会说这条看起来更好些。与此同时，你可以试验第三种模型，其可能产生一条像这样的学习曲线（红色曲线），还有另一条（绿色曲线），也许这条有所偏离，像这样，等等。或者你可以同时平行试验许多不同的模型，橙色的线就是不同的模型。用这种方式你可以试验许多不同的参数设定，然后只是最后快速选择工作效果最好的那个。在这个例子中，也许这条看起来是最好的（下方绿色曲线）。

打个比方，我把左边的方法称为熊猫方式。当熊猫有了孩子，他们的孩子非常少，一次通常只有一个，然后他们花费很多精力抚养熊猫宝宝以确保其能成活，所以，这的确是一种照料，一种模型类似于一只熊猫宝宝。对比而言，右边的方式更像鱼类的行为，我称之为鱼子酱方式。在交配季节，有些鱼类会产下一亿颗卵，但鱼类繁殖的方式是，它们会产生很多卵，但不对其中任何一个多加照料，只是希望其中一个，或其中一群，能够表现出色。我猜，这就是哺乳动物繁衍和鱼类，很多爬虫类动物繁衍的区别。我将称之为熊猫方式与鱼子酱方式，因为这很有趣，更容易记住。

所以这两种方式的选择，是由你拥有的计算资源决定的，如果你拥有足够的计算机去平行试验许多模型，那绝对采用鱼子酱方式，尝试许多不同的超参数，看效果怎么样。但在一些应用领域，比如在线广告设置和计算机视觉应用领域，那里的数据太多了，你需要试验大量的模型，所以同时试验大量的模型是很困难的，它的确是依赖于应用的过程。但我看到那些应用熊猫方式多一些的组织，那里，你会像对婴儿一样照看一个模型，调试参数，试着让它工作运转。尽管，当然，甚至是在熊猫方式中，试验一个模型，观察它工作与否，也许第二或第三个星期后，也许我应该建立一个不同的模型（绿色曲线），像熊猫那样照料它，我猜，这样一生中可以培育几个孩子，即使它们一次只有一个孩子或孩子的数量很少。

所以希望你能学会如何进行超参数的搜索过程，现在，还有另一种技巧，能使你的神经网络变得更加坚实，它并不是对所有的神经网络都适用，但当适用时，它可以使超参数搜索变得容易许多并加速试验过程，我们在下一节中再讲解这个技巧。

归一化网络的激活函数（Normalizing activations in a network）

在深度学习兴起后，最重要的一个思想是它的一种算法，叫做 Batch 归一化，由 Sergey loffe 和 Christian Szegedy 两位研究者创造。Batch 归一化会使你的参数搜索问题变得很容易，使神经网络对超参数的选择更加稳定，超参数的范围会更加庞大，工作效果也很好，也会使你的训练更加容易，即便是很深层的网络。让我们来看看 Batch 归一化是怎么起作用的吧。

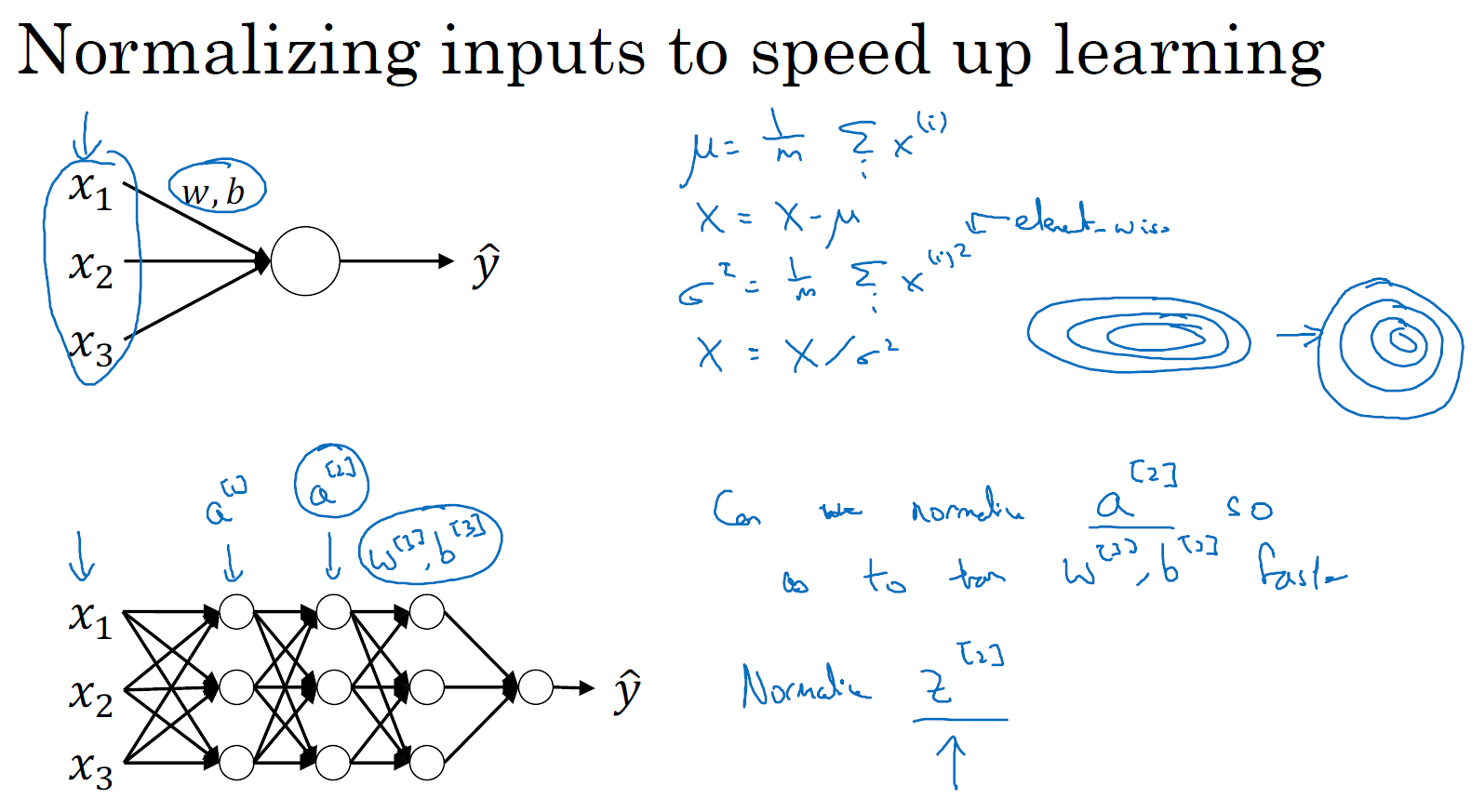
当训练一个模型，比如 logistic 回归时，你也许会记得，归一化输入特征可以加快学习过程。你计算了平均值，从训练集中减去平均值，计算了方差，接着根据方差归一化你的数据集，在之前的课程中我们看到，这是如何把学习问题的轮廓，从很长的椭圆的东西，变成更圆的东西，更易于算法优化。所以对于 logistic 回归和神经网络的归一化输入特征值而言，这是有效的。

那么更深的模型呢？你不仅输入了特征值 \(x\)，而且对于网络的第一层还有激活值 \(a^{[1]}\)，对于网络的第二层还有激活值 \(a^{[2]}\) 等等。如果你想训练这些参数，比如 \(w^{[3]}\)，\(b^{[3]}\)，那归一化 \(a^{[2]}\) 的平均值和方差岂不是很好？以便使 \(w^{[3]}\)，\(b^{[3]}\) 的训练更有效率。在 logistic 回归的例子中，我们看到了如何归一化 \(x_{1}\)，\(x_{2}\)，\(x_{3}\)，会帮助你更有效的训练 \(w\) 和 \(b\)。

所以问题来了，对任何一个隐藏层而言，我们能否归一化激活函数 \(a\) 的值，在此例中，比如说归一化 \(a^{[2]}\) 的值，以便更快速的训练 \(w^{[3]}\)，\(b^{[3]}\)，因为 \(a^{[2]}\) 是下一层的输入值，所以就会影响 \(w^{[3]}\)，\(b^{[3]}\) 的训练。简单来说，这就是 Batch 归一化的作用。尽管严格来说，我们真正归一化的不是 \(a^{[2]}\)，而是 \(z^{[2]}\)，深度学习文献中有一些争论，关于在激活函数之前是否应该将值 \(z^{[2]}\) 归一化，或是否应该在应用激活函数 \(a^{[2]}\) 后再归一化。实践中，经常做的是归一化 \(z^{[2]}\)，所以这就是我介绍的版本，我推荐其为默认选择，那下面就是 Batch 归一化的使用方法。

在神经网络的 \(l\) 层中，已知一些隐藏单元的中间值，从 \(z^{[l](1)}\) 到 \(z^{[l](m)}\)，然后用之前常用的那个公式计算方差，接着，你会取每个 \(z^{[l](i)}\) 值，使其规范化，即：减去均值再除以标准差，为了使数值稳定，通常将 \(\varepsilon\) 作为分母，以防 \(\sigma = 0\) 的情况。

\(\mu = \frac{1}{m}\sum\limits_{i}Z^{[l](i)}\)
\(\sigma^2 = \frac{1}{m}\sum\limits_{i}\left(Z^{[l](i)} - \mu \right)^2\)
\(Z_{norm}^{[l](i)} = \frac{Z^{[l](i)} - \mu}{\sqrt{\sigma^2 + \varepsilon}}\)

所以现在我们已把这些 \(z\) 值标准化为 0 平均值和标准单位方差，但我们不想让隐藏单元总是含有平均值 0 和方差 1，也许隐藏单元有了不同的分布会更有意义，所以我们更希望可以自由的控制其均值和方差。具体做法就是计算，我们称之为 \({\tilde{z}}^{(i)}\)，\({\tilde{z}}^{(i)} = \gamma \; z_{norm}^{(i)} + \beta\)，这里 \(\gamma\) 和 \(\beta\) 是你模型中可学习的参数（learnable parameters），类似于 \(w\) 和 \(b\)，所以之后我们会使用梯度下降或一些其它类似梯度下降的算法，比如 Momentum，Nesterov 或者 Adam，你会不断的更新 \(\gamma\) 和 \(\beta\)，正如更新神经网络的权重 \(w\) 和 \(b\) 一样。

请注意 \(\gamma\) 和 \(\beta\) 的作用是，你可以随意设置 \({\tilde{z}}^{(i)}\) 的平均值以及方差，事实上，如果 \(\gamma= \sqrt{\sigma^{2} +\varepsilon}\)，\(\beta\) 等于 \(\mu\)，那么 \({\tilde{z}}^{(i)} = z^{(i)}\)。所以通过对 \(\gamma\) 和 \(\beta\) 的合理设定，从根本来说它只是在计算恒等函数，将会使你可以构造出含有其它平均值和方差的隐藏单元值。

所以，现在网络匹配这个单元的方式，之前可能是用 \(z^{(1)}\)，\(z^{(2)}\) 等等，现在则会用 \({\tilde{z}}^{(i)}\) 取代 \(z^{(i)}\)，以方便神经网络中的后续计算。如果你想放回 \([l]\)，以清楚的表明它位于哪一层，你可以使用 \(z^{[l](i)}\)。

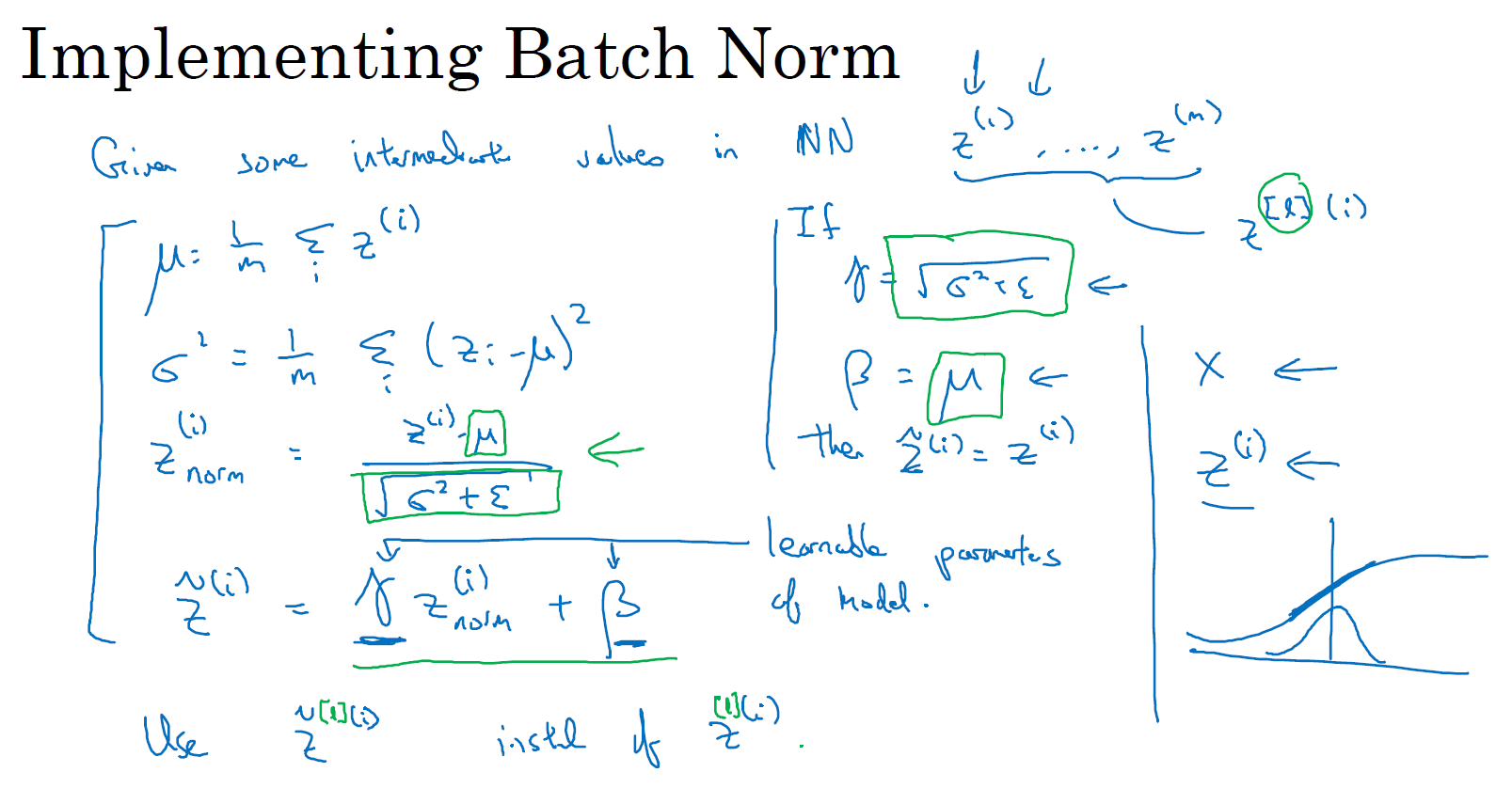
所以我希望你学到的是，归一化输入特征 \(X\) 是怎样有助于神经网络学习的，而 Batch 归一化的作用是它适用的归一化过程，不只是输入层，甚至同样适用于神经网络中的深度隐藏层。你应用 Batch 归一化了一些隐藏单元值中的平均值和方差，不过训练输入和这些隐藏单元值的一个区别是，你也许不想隐藏单元值必须是平均值 0 和方差 1。

比如，假设你有 sigmoid 激活函数，你不想让你的值总是全部集中在这里，你想使它们有更大的方差，或不是 0 的平均值，以便更好的利用非线性的 sigmoid 函数，而不是使所有的值都集中于这个线性版本中，这就是为什么有了 \(\gamma\) 和 \(\beta\) 两个参数后，学习算法可以将 \(\tilde{z}^{(i)}\) 设置为任何值，所以它真正的作用是，使隐藏单元值的均值和方差标准化，即 \(\tilde{z}^{(i)}\) 有固定的均值和方差，均值和方差可以是 0 和 1，也可以是其它值，它是由 \(\gamma\) 和 \(\beta\) 两参数控制的。

我希望你能学会怎样使用 Batch 归一化，至少就神经网络的单一层而言，在下一节中，我会教你如何将 Batch 归一化与神经网络甚至是深度神经网络相匹配。对于神经网络许多不同层而言，又该如何使它适用，之后，我会告诉你，Batch 归一化有助于训练神经网络的原因。所以如果觉得 Batch 归一化起作用的原因还显得有点神秘，那跟着我走，在接下来的两节课程中，我们会弄清楚。

将 Batch Norm 拟合进神经网络（Fitting Batch Norm into a neural network）

上一节，我们探讨了如何在单一隐藏层进行 Batch 归一化，接下来，让我们看看如何将它拟合进深度神经网络的训练中。

正如之前所讲过的，你可以认为神经网络中的每个单元负责计算两件事。第一，它先计算 \(z\)，然后应用其到激活函数中再计算 \(a\)。所以如果你没有应用 Batch 归一化，你会把输入 \(X\) 拟合到第一个隐藏层，然后首先计算 \(z^{[1]}\)，这是由 \(w^{[1]}\) 和 \(b^{[1]}\) 两个参数控制的。接着，通常而言，你会把 \(z^{[1]}\) 拟合到激活函数以计算 \(a^{[1]}\)。但 Batch 归一化的做法是将 \(z^{[1]}\) 值进行 Batch 归一化，简称 BN，此过程将由 \({\beta}^{[1]}\) 和 \(\gamma^{[1]}\) 两参数控制，这一操作会给你一个新的规范化的 \(z^{[1]}\) 值（\({\tilde{z}}^{[1]}\)），然后将其输入激活函数中得到 \(a^{[1]}\)，即 \(a^{[1]} = g^{[1]}({\tilde{z}}^{[ l]})\)。现在，你已在第一层进行了计算，此时 BN 作用在 \(z^{[1]}\) 上，接下来，你需要应用 \(a^{[1]}\) 值来计算 \(z^{[2]}\)，此过程是由 \(w^{[2]}\) 和 \(b^{[2]}\) 控制的。与你在第一层所做的类似，你会将 \(z^{[2]}\) 进行 BN 操作，这是由下一层的 Batch 归一化参数所管制的，即 \({\beta}^{[2]}\) 和 \(\gamma^{[2]}\)，现在你得到 \({\tilde{z}}^{[2]}\)，再通过激活函数计算出 \(a^{[2]}\) 等等。

需要澄清的是，这里的这些 \(\beta\)（\({\beta}^{[1]}\)，\({\beta}^{[2]}\) 等等）和应用于 Momentum、Adam、RMSprop 等算法中的超参数 \(\beta\) 没有任何关系。Adam 论文的作者，在论文里用 \(\beta\) 代表超参数。Batch 归一化论文的作者，也使用了 \(\beta\) 代表此参数，但这是两个完全不同的 \(\beta\)。我在两种情况下都决定使用\(\beta\)，以方便你更容易阅读那些原创的论文。

所以，现在你的网络里不但有参数 \(w\)，\(b\)，而且还增加了两个新成员 \(\beta\) 和 \(\gamma\)。接下来你就可以使用想用的任何一种优化算法，比如使用梯度下降法来执行它。

举个例子，对于给定层，你会反向传播计算出 \(d{\beta}^{[l]}\)，接着更新参数 \(\beta\) 为 \({\beta}^{[l]} = {\beta}^{[l]} - \alpha d{\beta}^{[l]}\)。你也可以使用 Adam 或 RMSprop 或 Momentum，以更新参数 \(\beta\) 和 \(\gamma\)。

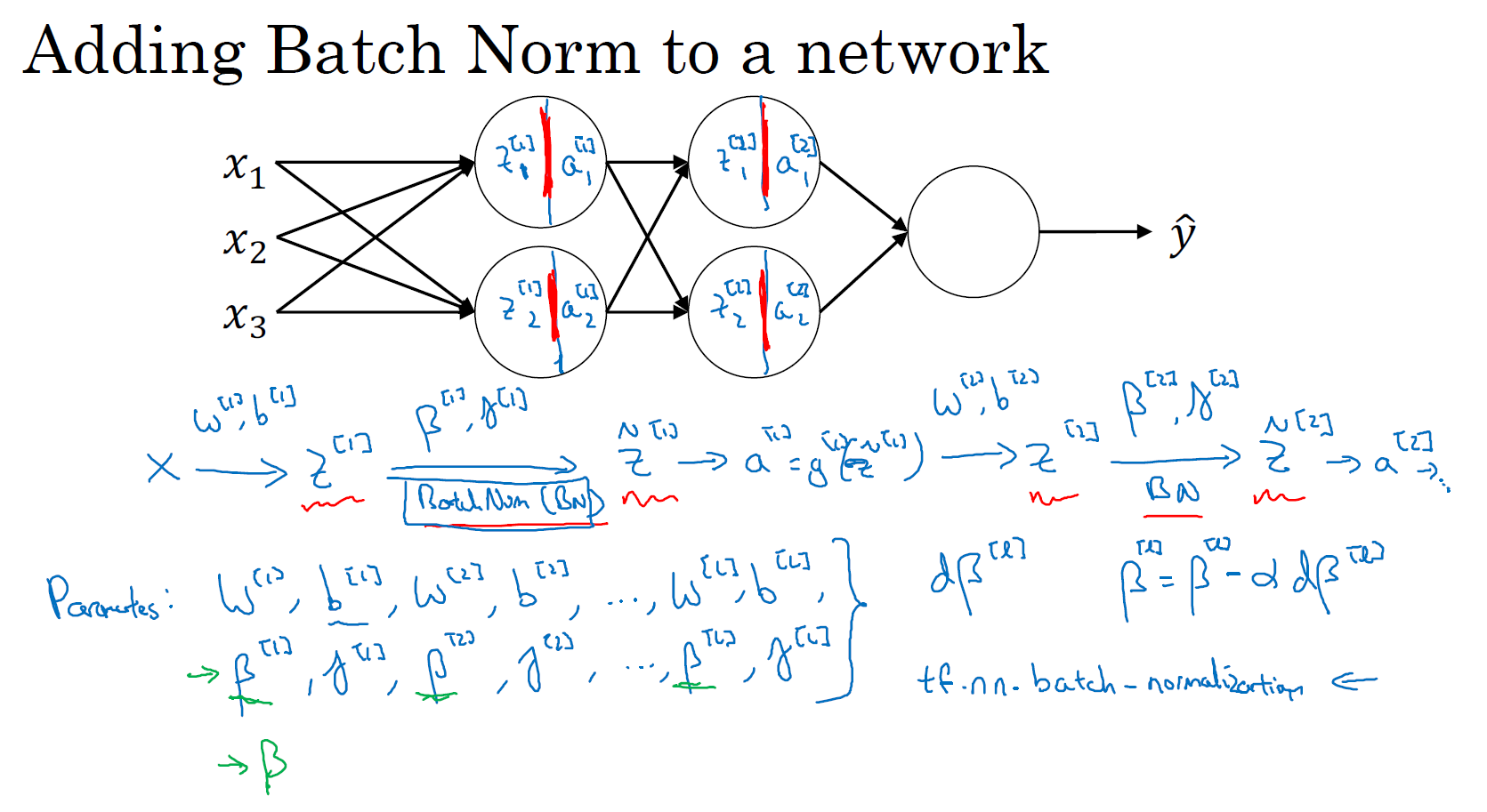
在深度学习编程框架中，对于 Batch 归一化的操作，通常只是一行代码。比如说，在 TensorFlow 框架中，你可以用这个函数 tf.nn.batch_normalization 来实现 Batch 归一化，我们稍后讲解，所以在实践中，你不必自己操作所有这些具体的细节，但知道它是如何作用的，你可以更好的理解代码的作用。

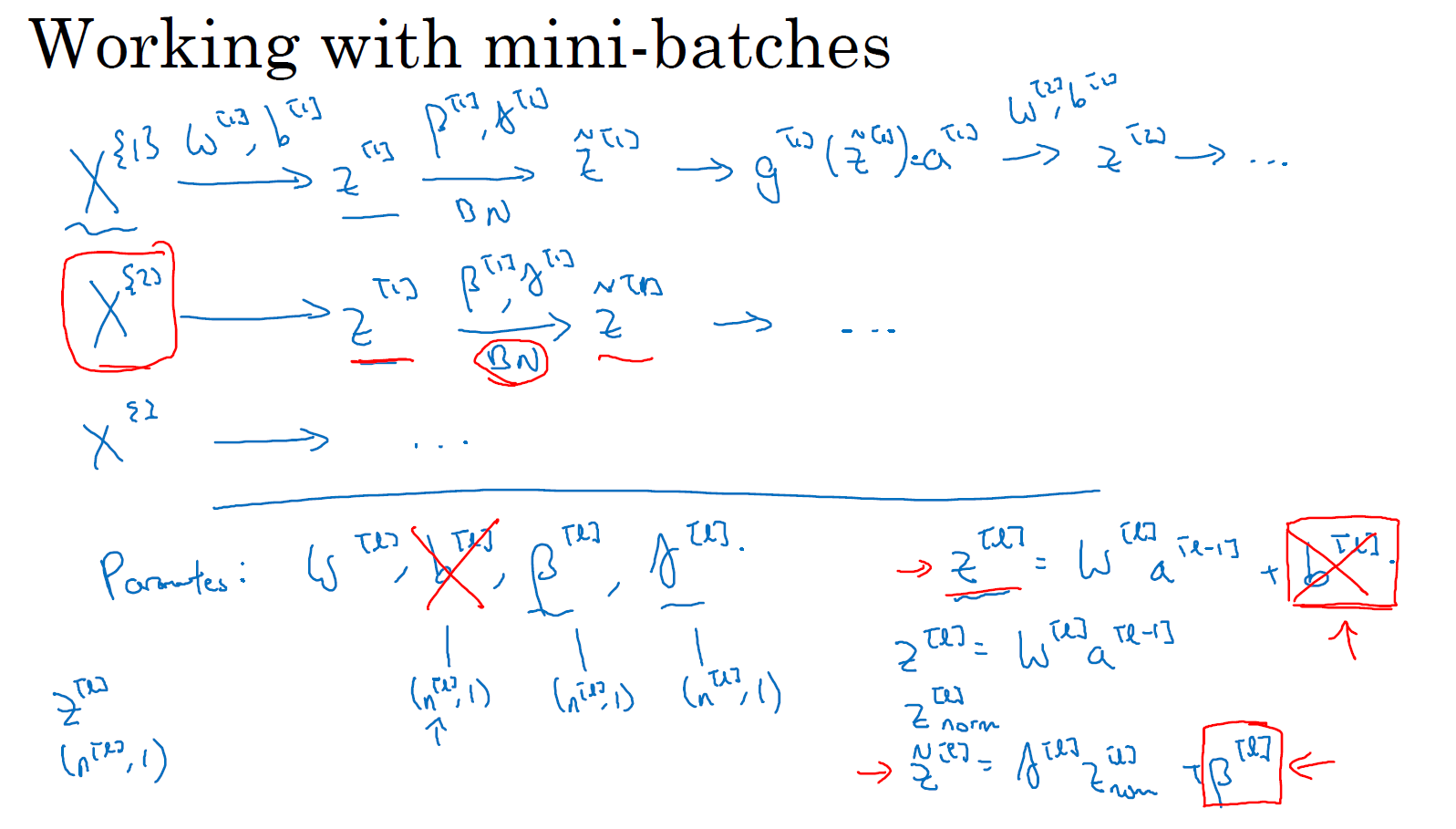
实践中，Batch 归一化通常和训练集的 mini-batch 一起使用。你应用 Batch 归一化的方式就是，使用第一个 mini-batch (\(X^{\{1\}}\))，然后应用参数 \(w^{[1]}\) 和 \(b^{[1]}\) 计算出 \(z^{[1]}\)。接着使用 \({\beta}^{[1]}\) 和 \(\gamma^{[1]}\) 对 \(z^{[1]}\) 执行 BN 操作，使其重新缩放，这样就得到了 \({\tilde{z}}^{[1]}\)，然后再应用激活函数得到 \(a^{[1]}\)。接着使用 \(w^{[2]}\) 和 \(b^{[2]}\) 计算 \(z^{[2]}\)，等等，而所有的这些都是在第一个 mini-batch 的基础上进行的一步梯度下降法。然后，以同样的操作继续第二个 mini-batch (\(X^{\{2\}}\))，第三个 mini-batch (\(X^{\{3\}}\)) ...

现在，我想澄清此参数的一个细节。先前我说过每层的参数是 \(w^{[l]}\) 和 \(b^{[l]}\)，还有 \({\beta}^{[l]}\) 和 \(\gamma^{[l]}\)。请注意计算 \(z\) 的方式是，\(z^{[l]} = w^{[l]}a^{\left\lbrack l - 1 \right\rbrack} +b^{[l]}\)，但 Batch 归一化做的是，对于这个 mini-batch，先将 \(z^{[l]}\) 归一化，结果为均值 0 和标准方差，再由 \(\beta\) 和 \(\gamma\) 重缩放，但这意味着，无论 \(b^{[l]}\) 的值是多少，都是要被减去的，因为在 Batch 归一化的过程中，你要计算 \(z^{[l]}\) 的均值，再减去平均值，在此例中的 mini-batch 中增加任何常数，数值都不会改变，因为加上的任何常数都将会被均值减去所抵消。所以，如果你在使用 Batch 归一化，其实你可以消除这个参数 \(b^{[l]}\)，或者你也可以，暂时把它设置为 0，那么，参数变成 \(z^{[l]} = w^{[l]}a^{\left\lbrack l - 1 \right\rbrack}\)，然后你计算归一化的 \(z^{[l]}\)，\({\tilde{z}}^{[l]} = \gamma^{[l]}z^{[l]} + {\beta}^{[l]}\)，你最后会用参数 \({\beta}^{[l]}\) 来决定 \({\tilde{z}}^{[l]}\) 的取值。所以总结一下，因为 Batch 归一化超过了此层 \(z^{[l]}\) 的均值，\(b^{[l]}\) 这个参数没有意义，所以，你必须去掉它，由 \({\beta}^{[l]}\) 代替，这是个控制参数，会影响到均值转移或偏置的条件。

最后，确认下维度， \(z^{[l]}\) 的维度是 \((n^{[l]},1)\)，\(b^{[l]}\) 的维度是 \((n^{[l]},1)\)，如果 \(n^{[l]}\) 是 \(l\) 层隐藏单元的数量，那么 \({\beta}^{[l]}\) 和 \(\gamma^{[l]}\) 的维度也是 \((n^{[l]},1)\)。

让我们总结一下关于如何用 Batch 归一化来应用梯度下降法，假设你在使用 mini-batch 梯度下降法，你运行 \(t=1\) 到 batch 数量的 for 循环，你会在 mini-batch \(X^{\{t\}}\) 上应用正向 prop，每个隐藏层都应用正向 prop，用 Batch 归一化代替 \(z^{[l]}\) 为 \({\tilde{z}}^{[l]}\)。接下来，它确保在这个 mini-batch 中，\(z\) 值有归一化的均值和方差，归一化均值和方差后是 \({\tilde{z}}^{[l]}\)，然后，你用反向 prop 计算 \(dw^{[l]}\) 和 \(db^{[l]}\)，及所有 \(l\) 层所有的参数，\(d{\beta}^{[l]}\) 和 \(d\gamma^{[l]}\)。尽管严格来说，因为你要去掉 \(b\)，这部分其实已经去掉了。最后，你更新这些参数：\(w^{[l]} = w^{[l]} - \alpha \mathrm{d}w^{[l]}\)，和以前一样，\({\beta}^{[l]} = {\beta}^{[l]} - \alpha \mathrm{d} \beta^{[l]}\)，对于 \(\gamma\) 也是如此 \(\gamma^{[l]} = \gamma^{[l]} - \alpha \mathrm{d} \gamma^{[l]}\)。

上面使用的是标准的 mini-batch 梯度下降法，你也可以使用其它的算法来更新，比如选择使用 Momentum、RMSprop、Adam 的梯度下降法来更新由 Batch 归一化添加到算法中的 \(\beta\) 和 \(\gamma\) 参数。

希望你已经能够从头开始应用 Batch 归一化了，但实践中，你可以直接调用别人的编程框架，这会使 Batch 归一化的使用变得很容易。

现在，以防 Batch 归一化仍然看起来有些神秘，尤其是你还不清楚为什么其能如此显著的加速训练，我们进入下一节，详细讨论 Batch 归一化为何效果如此显著，它到底在做什么。

为什么Batch Norm奏效？（Why does Batch Norm work?）

1. Feature Scaling，加速梯度下降法的收敛

正如你之前看到的，归一化输入特征值 \(x\)，使其均值为 0，方差 1，所以你会有一些从 0 到 1 而不是从 1 到 1000 的特征值，通过归一化所有的输入特征值 \(x\)，以获得类似范围的值，可以加速学习。所以 Batch 归一化起作用的原因，直观的一点就是它也在做类似的工作，但不仅仅对于输入值，还有隐藏单元的值，这只是 Batch 归一化作用的冰山一角，还有些深层的原理，它会有助于你对 Batch 归一化的作用有更深的理解，让我们一起来看看吧。

2. Use Batch Norm to fix Covariate shift problem

数据改变了分布，叫做 "Covariate shift"。举个例子，假设给定一个神经网络，用来区分是猫或不是猫。你的训练集中全部都是黑猫，但是如果你现在要把这个模型应用到有颜色的猫上面，这个模型可能适应的不会很好。因为输入数据的分布被改变了。这时候你可能需要重新学习模型。

Batch 归一化做的是它限制了网络中前一层的参数更新，会影响输出的数值分布的程度，迫使后层适应的程度减小了，你可以这样想，它减弱了前层参数的作用与后层参数的作用之间的联系，它使得网络每层都可以自己学习，稍稍独立于其它层，这有助于加速整个网络的学习。所以，希望这能带给你更好的直觉，尤其从神经网络后层的角度而言，前层不会左右移动的那么多，因为它们被同样的均值和方差所限制，所以，这会使得后层的学习工作变得更容易些。

3. Batch Norm as regularization

Batch 归一化还有一个作用，它有轻微的正则化效果。

在一个 mini-batch 上执行 Batch 归一化的过程中，由于此时计算的均值和方差，不是在整个数据集上计算得来的，所以会产生一些小的噪声，然后接着在缩放的过程中，从 \(z^{[l]}\) 到 \({\tilde{z}}^{[l]}\) 也会有一些噪音，因为它是用已经存在噪音的均值和方差计算得出的。

所以和 dropout 相似，它往每个隐藏层的激活值上增加了噪音，dropout 有增加噪音的方式，它使一个隐藏的单元，以一定的概率乘以 0，以一定的概率乘以 1，所以你的 dropout 含有几重噪音。

对比而言，Batch 归一化也含有几重噪音，因为均值和标准差的估计值是有噪音的，所以类似于 dropout，Batch 归一化有轻微的正则化效果，因为给隐藏单元添加了噪音，这迫使后面的单元不过分依赖任何一个隐藏单元。因为添加的噪音很微小，所以并不是巨大的正则化效果，如果你想得到更强大的正则化效果，你可以将 Batch 归一化和 dropout 一起使用。

也许另一个轻微非直观的效果是，如果你应用了较大的 mini-batch，比如说，你用了 512 而不是 64，通过应用较大的 min-batch，你就减少了噪音，因此减少了正则化效果，这也是 dropout 的一个奇怪的性质，就是应用较大的 mini-batch 可以减少正则化效果。

说到这儿，我把 Batch 归一化当成了一种正则化，这确实不是其目的，但有时它会对你的算法有额外的期望效应或非期望效应。但是不要把 Batch 归一化当作正则化，把它当作将你归一化隐藏单元激活值并加速学习的方式，我认为正则化几乎是一个意想不到的副作用。

所以希望这能让你更理解 Batch 归一化的工作原理，在我们结束 Batch 归一化的讨论之前，我想确保你还知道一个细节。Batch 归一化一次只能处理一个 mini-batch 的数据，它在 mini-batch 上计算均值和方差。所以测试时，你试图做出预测，试着评估神经网络，你也许没有一个 mini-batch 的例子，可能一次只能进行一个简单的例子的预测，所以测试时，你需要做一些不同的东西以确保你的预测有意义。

在下一节中，让我们详细谈谈你需要注意的一些细节，让你的神经网络应用 Batch 归一化来做出预测。

测试时的 Batch Norm（Batch Norm at test time）

Batch 归一化将你的数据以 mini-batch 的形式逐一处理，但在测试时，你可能需要对每个样本逐一处理，我们来看一下怎样调整你的网络来做到这一点。

\(\mu = \frac{1}{m}\sum\limits_{i}Z^{[l](i)}\)

\(\sigma^2 = \frac{1}{m}\sum\limits_{i}\left(Z^{[l](i)} - \mu \right)^2\)

\(Z_{norm}^{[l](i)} = \frac{Z^{[l](i)} - \mu}{\sqrt{\sigma^2 + \varepsilon}}\)

\({\tilde{z}}^{[l](i)} = \gamma \; z_{norm}^{[l](i)} + \beta\)

回想一下，在训练时，这些就是用来执行 Batch 归一化的等式。在一个 mini-batch 中，你将 mini-batch 的 \(z^{(i)}\) 值求和，计算均值，所以这里你只把一个 mini-batch 中的样本都加起来，我用 \(m\) 来表示这个 mini-batch 中的样本数量，而不是整个训练集。然后计算方差，再算 \(z_{norm}^{(i)}\)，即用均值和标准差来调整，加上 \(\varepsilon\) 是为了数值稳定性。\(\tilde{z}\) 是用 \(\gamma\) 和 \(\beta\) 再次调整 \(z_{norm}\) 得到的。

请注意用于调节计算的 \(\mu\) 和 \(\sigma^{2}\) 是在整个 mini-batch 上进行计算，但是在测试时，你可能不能将一个 mini-batch 中的 64 或 128 个样本同时处理，因此你需要用其它方式来得到 \(\mu\) 和 \(\sigma^{2}\)，而且如果你只有一个样本，一个样本的均值和方差没有意义。那么实际上，为了将你的神经网络应用于预测，就需要单独估算 \(\mu\) 和 \(\sigma^{2}\)，在 典型 的 Batch 归一化应用中，你需要用一个 指数加权平均 来估算，这个平均数涵盖了所有 mini-batch，接下来我会具体解释。

我们选择 \(l\) 层，假设我们有 mini-batch，\(X^{\{1\}}\)，\(X^{\{2\}}\)，\(X^{\{3\}}\)……以及对应的 \(y\) 值等等，那么在为 \(l\) 层训练 \(X^{\{1\}}\) 时，你就得到了 \(\mu^{\{1\}[l]}\)。当你训练第二个 mini-batch，你就会得到 \(\mu^{\{2\}[l]}\)。然后在这一隐藏层的第三个 mini-batch，你得到了第三个 \(\mu^{\{3\}[l]}\)。正如我们之前用的指数加权平均来计算 \(\theta_{1}\)，\(\theta_{2}\)，\(\theta_{3}\) 的均值，当时是试着计算当前气温的指数加权平均，你会这样来追踪你看到的这个均值向量的最新平均值，于是这个指数加权平均就成了你对这一隐藏层的 \(z\) 均值的估值。同样的，你可以用指数加权平均来追踪你在这一层的第一个 mini-batch 中所见的 \(\sigma^{2}\) 的值，以及第二个 mini-batch 中所见的 \(\sigma^{2}\) 的值等等。因此在用不同的 mini-batch 训练神经网络的同时，能够得到你所查看的每一层的 \(\mu\) 和 \(\sigma^{2}\) 的平均数的实时数值。

最后在测试时，对应这个等式 \(z_{norm} = \frac{z - \mu}{\sqrt{\sigma^{2} + \varepsilon}}\)，你只需要用你的 \(z\) 值来计算 \(z_{norm}\)，用你手头的最新的 \(\mu\) 和 \(\sigma^{2}\) 的指数加权平均数值来做调整，然后你可以用刚算出来的 \(z_{norm}\) 和你在神经网络训练过程中得到的 \(\beta\) 和 \(\gamma\) 参数来计算你那个测试样本的\(\tilde{z}\) 值。

总结一下就是，在训练时，\(\mu\) 和 \(\sigma^{2}\) 是在整个 mini-batch 上计算出来的包含了像是 64 或 128 或其它一定数量的样本，但在测试时，你可能需要逐一处理样本，方法是根据你的训练集估算 \(\mu\) 和 \(\sigma^{2}\)，估算的方式有很多种，理论上你可以在最终的网络中运行整个训练集来得到 \(\mu\) 和 \(\sigma^{2}\)，但在实际操作中，我们通常运用指数加权平均来追踪在训练过程中你看到的 \(\mu\) 和 \(\sigma^{2}\) 的值。还可以用移动平均来粗略估算 \(\mu\) 和 \(\sigma^{2}\)，然后在测试中使用 \(\mu\) 和 \(\sigma^{2}\) 的值来进行你所需要的隐藏单元 \(z\) 值的调整。在实践中，不管你用什么方式估算 \(\mu\) 和 \(\sigma^{2}\)，这套过程都是比较稳健的，因此我不太会担心你具体的操作方式，而且如果你使用的是某种深度学习框架，通常会有默认的估算 \(\mu\) 和 \(\sigma^{2}\) 的方式，应该一样会起到比较好的效果。但在实践中，任何合理的估算你的隐藏单元 \(z\) 值的均值和方差的方式，在测试中应该都会有效。

Batch 归一化就讲到这里，使用 Batch 归一化，你能够训练更深的网络，让你的学习算法运行速度更快，在结束这周的课程之前，我还想和你们分享一些关于深度学习框架的想法，让我们在下一节中一起讨论这个话题。

Softmax 回归（Softmax Regression）

到目前为止，我们讲到过的分类的例子都使用了二分分类，这种分类只有两种可能的标记0或1，这是一只猫或者不是一只猫，如果我们有多种可能的类型的话呢？有一种 logistic 回归的一般形式，叫做 Softmax 回归，能让你在试图识别某一分类时做出预测，或者说是多种分类中的一个，不只是识别两个分类，我们来一起看一下。

假设你不单需要识别猫，而是想识别猫，狗和小鸡，我把猫加做类 1，狗为类 2，小鸡是类 3，如果不属于以上任何一类，就分到 "其它" 或者说 "以上均不符合" 这一类，我把它叫做类 0。上面显示的图片及其对应的分类就是一个例子。

我们用大写的 \(C\) 来表示你的输入会被分入的类别总个数，在这个例子中，我们有 4 种可能的类别，包括 "其它" 或 "以上均不符合" 这一类。当有 4 个分类时，指示类别的数字，就是从 0 到 \(C-1\)，换句话说就是0、1、2、3。

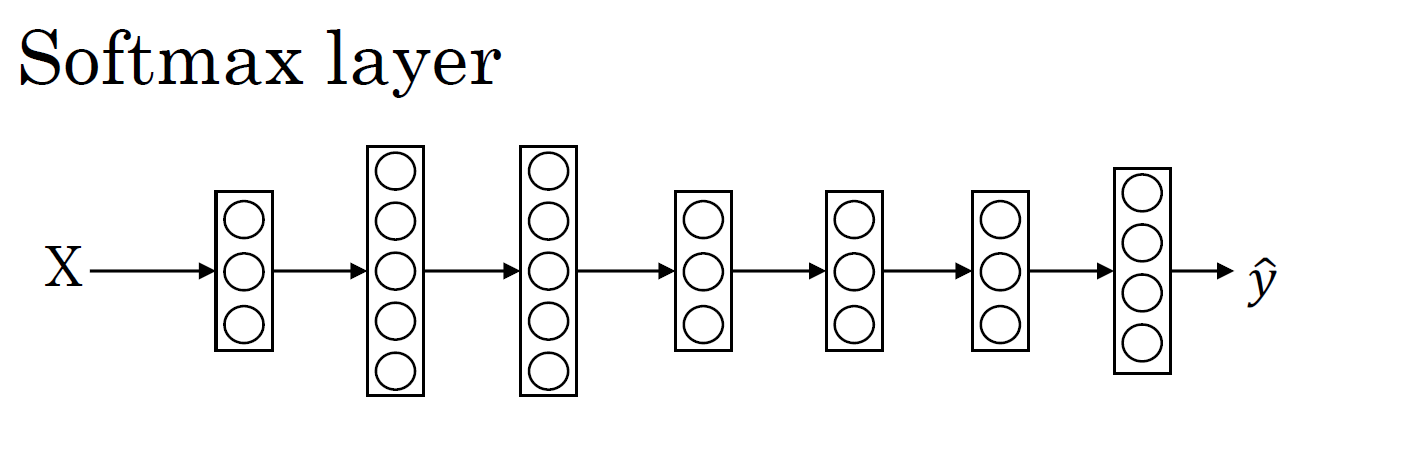
在这个例子中，我们将建立一个神经网络，其输出层有 4 个，或者说 \(C\) 个输出单元，因此 \(n\)，即输出层也就是 \(L\) 层的单元数量，等于4，或者一般而言等于 \(C\)。我们想要输出层单元的数字告诉我们这 4 种类型中每个的概率有多大，所以:

• \(L\) 层第一个单元（圆圈）输出的应该是或者说我们希望它输出 "其它" 类的概率。
• \(L\) 层第二个单元（圆圈）输出猫的概率。
• \(L\) 层第三个单元（圆圈）输出狗的概率。
• \(L\) 层第四个单元（圆圈）输出输出小鸡的概率，把小鸡缩写为bc（baby chick）。

因此这里的 \(\hat y\) 将是一个 \(4×1\) 维向量，因为它必须输出四个数字，给你这四种概率，而且输出中的四个数字加起来应该等于1。让你的网络做到这一点的标准模型需要用到 Softmax 层来生成输出。在这一层，你将会像往常一样计算各个单元的线性部分，\(z^{[L]}\) 这是最后一层的 \(z\) 变量，记住这是大写 \(L\) 层，和往常一样，计算方法是 \(z^{[L]} = W^{[L]}a^{[L-1]} + b^{[L]}\)，算出了 \(z\) 之后，你需要应用 Softmax 激活函数，但和以往的激活函数不同的是，我们要把这四个单元的 \(z\) 一起输入到 Softmax 激活函数中，一起计算，然后生成一个 \(4 \times 1\) 的输出。我们之前的激活函数都是接受单行数值输入，例如 Sigmoid 和 ReLu 激活函数，输入一个实数，输出一个实数。但对于 Softmax 激活函数而言，因为需要将所有可能的输出归一化，就需要输入一个向量，最后输出一个向量。

具体的计算公式为 ：\(a_{i}^{[L]} = \frac{e^{z^{[L]}_i}}{\sum\limits_{j = 1}^{4}e^{z^{[L]}_i}}\)

我们来看一个具体的例子，假设你算出了 \(z^{[L]}\)，\(z^{[L]}\)是一个 \(4 \times 1\) 的向量：
\(z^{[L]} = \begin{bmatrix} 5 & 2 & - 1 & 3 \end{bmatrix}\)

接下来我们要做的就是用这个元素取幂方法来计算 \(e^{z^{[L]}}\)
\(e^{z^{[L]}} =\begin{bmatrix} e^{5} & e^{2} & e^{-1} & e^{3} \end{bmatrix}=\begin{bmatrix} 148.4 & 7.4 & 0.4 & 20.1 \end{bmatrix}\)

最后，如果我们想从向量 \(e^{z^{[L]}}\) 得到向量 \(a^{[L]}\) 就只需要将这些项目归一化，使总和为1。
如果把 \(e^{z^{[L]}}\) 的元素都加起来，那么总和是 176.3
所以最终 \(a^{[L]} = \frac{e^{z^{[L]}}}{176.3} = \frac{\begin{bmatrix} 148.4 & 7.4 & 0.4 & 20.1 \end{bmatrix}}{176.3} = \begin{bmatrix} 0.842 & 0.042 & 0.002 & 0.114 \end{bmatrix}\)。

所以，它是类 0 的概率为 84.2%，是类 1 的概率为 4.2%，是类 2 的概率为 0.2%，是类 3 的概率为 11.4%。本例中因为类 0 的概率最大，那么预测的结果就是类 0。

那么 Softmax 分类器还可以代表其它的什么东西么？我来举几个例子，你有两个输入\(x_{1}\), \(x_{2}\)，将它们直接输入到 Softmax 层。

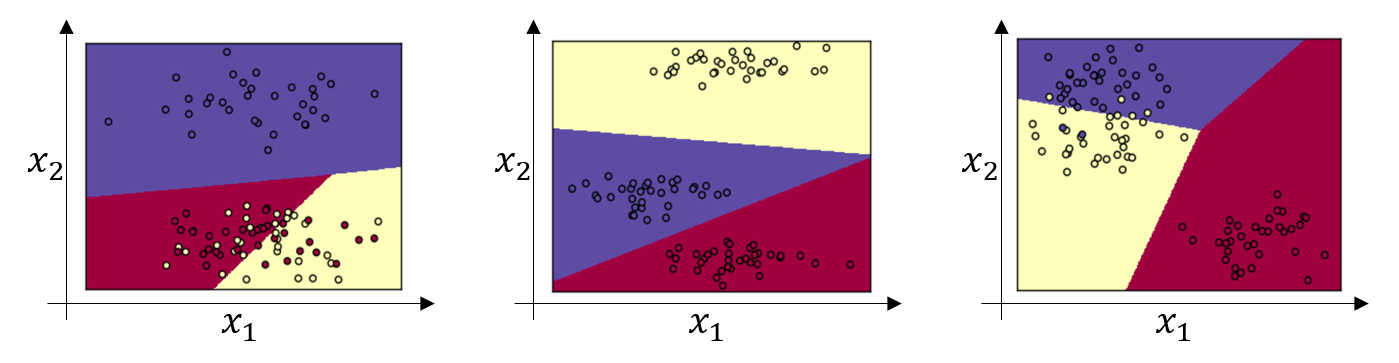
这个例子中是三个有 \(C=3\) 个输出分类的 Softmax 层所代表的决策边界，请注意图中的几条线性决策边界（任何两个分类之间的决策边界都是线性的），这使得它能够将数据分到 3 个类别中，图中的颜色显示了 Softmax 分类器输出的阈值，其着色是基于三种输出中概率最高的那种。因此我们可以看到这是 logistic 回归的一般形式，有类似线性的决策边界，但分类不只有 0 和 1，而是0，1，2。

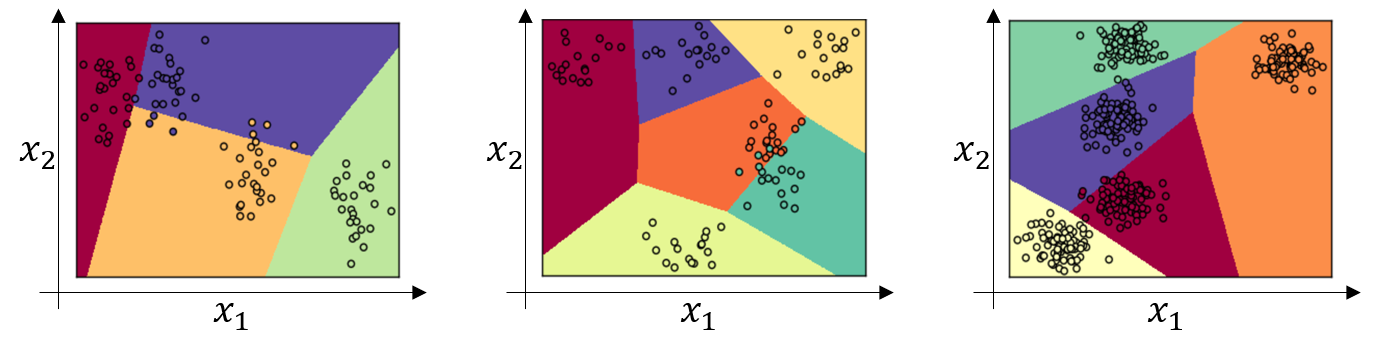
我们来看一下更多分类的例子，这个例子中（左边图）\(C=4\)，（中间图）是 \(C=6\) ，（右边图）是 \(C=5\)，这显示了 Softmax 分类器在没有隐藏层的情况下能够做到的事情，当然更深的神经网络会有 \(x\)，然后是一些隐藏单元，或者更多的隐藏层以及单元等等，如此就可以学习更复杂的非线性决策边界，来区分多种不同分类。

训练一个Softmax 分类器（Training a softmax classifier）

上节课中我们学习了 Softmax 层和 Softmax 激活函数，在本节课中，你将更深入地了解 Softmax 分类，并学习如何训练一个使用了 Softmax 层的模型。

Softmax and Hardmax

Softmax 这个名称的来源是与所谓 Hardmax 对比，Hardmax 会把向量 \(z\) 变成这个向量 \(\begin{bmatrix} 1 & 0 & 0 & 0 \end{bmatrix}\)，Hardmax 函数会观察 \(z\) 的元素，然后在 \(z\) 中最大元素的位置放上 1，其它位置放上 0。与之相反，Softmax 更为温和，它所做的从 \(z\) 到这些概率的映射，我不知道这是不是一个好名字，但至少这就是 Softmax 这一名称背后所包含的想法，与 Hardmax 正好相反。

Softmax regression generalizes logistic regression to C classes

有一点我没有细讲，但之前已经提到过的，就是 Softmax 回归或 Softmax 激活函数将 logistic 激活函数推广到 \(C\) 类，而不仅仅是两类，结果就是如果 \(C=2\)，那么 \(C=2\) 的 Softmax 实际上变回了 logistic 回归，我不会在本节课中给出证明，但是大致的证明思路是这样的，如果 \(C=2\)，并且你应用了 Softmax，那么输出层 \(a^{[L]}\) 将会输出两个数字，如果 \(C=2\) 的话，也许输出 0.842 和 0.158，对吧？这两个数字加起来要等于 1，因为它们的和必须为 1，其实它们是冗余的，也许你不需要计算两个，而只需要计算其中一个，结果就是你最终计算那个数字的方式又回到了 logistic 回归计算单个输出的方式。这算不上是一个证明，但我们可以从中得出结论，Softmax 回归将 logistic 回归推广到了两种分类以上。

训练带有 Softmax 输出层的神经网络

• for \(x \in \mathbb{R}^{1\times n}\), thus we have:
  $Softmax(x) = softmax(\begin{bmatrix}
  x_1 &
  x_2 &
  ... &
  x_n
  \end{bmatrix}) = \begin{bmatrix}
  \frac{e^{{x_1}}{\sum_{j}e}{x_j}} &
  \frac{e^{{x_2}}{\sum_{j}e}{x_j}} &
  ... &
  \frac{e^{{x_n}}{\sum_{j}e}{x_j}}
  \end{bmatrix} $

• for a matrix \(x \in \mathbb{R}^{m \times n}\), \(x_{ij}\) maps to the element in the \(i^{th}\) row and \(j^{th}\) column of \(x\), thus we have:

\[softmax(x) = softmax\begin{bmatrix} x_{11} & x_{12} & x_{13} & \dots & x_{1n} \\ x_{21} & x_{22} & x_{23} & \dots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & x_{m3} & \dots & x_{mn} \end{bmatrix} = \begin{bmatrix} \frac{e^{x_{11}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{12}}}{\sum_{j}e^{x_{1j}}} & \frac{e^{x_{13}}}{\sum_{j}e^{x_{1j}}} & \dots & \frac{e^{x_{1n}}}{\sum_{j}e^{x_{1j}}} \\ \frac{e^{x_{21}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{22}}}{\sum_{j}e^{x_{2j}}} & \frac{e^{x_{23}}}{\sum_{j}e^{x_{2j}}} & \dots & \frac{e^{x_{2n}}}{\sum_{j}e^{x_{2j}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{e^{x_{m1}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m2}}}{\sum_{j}e^{x_{mj}}} & \frac{e^{x_{m3}}}{\sum_{j}e^{x_{mj}}} & \dots & \frac{e^{x_{mn}}}{\sum_{j}e^{x_{mj}}} \end{bmatrix} = \begin{pmatrix} softmax\text{(first row of x)} \\ softmax\text{(second row of x)} \\ ... \\ softmax\text{(last row of x)} \\ \end{pmatrix} \]

接下来我们来看怎样训练带有 Softmax 输出层的神经网络，具体而言，我们先定义训练神经网络会使用到的损失函数。举个例子，我们来看看训练集中某个样本的目标输出，真实标签是\(y = \begin{bmatrix} 0 & 1 & 0 & 0 \end{bmatrix}\)，用上节课中讲到过的例子，这表示这是一张猫的图片，因为它属于类 1，现在我们假设你的神经网络输出的是 \(\hat y\)，\(\hat y\) 是一个包括总和为 1 的概率的向量，\(\hat y = \begin{bmatrix} 0.3 & 0.2 & 0.1 & 0.4 \end{bmatrix}\)，同时它也是 \(a^{[L]}\)，即 \(a^{[L]} = \hat y = \begin{bmatrix} 0.3 & 0.2 & 0.1 & 0.4\end{bmatrix}\)。对于这个样本神经网络的表现不佳，这实际上是一只猫，但却只分配到 20% 是猫的概率。

在 Softmax 分类中，我们一般用到的损失函数是 \(L(\hat y,y ) = - \sum\limits_{j = 1}^{C}{y_{j} \; log \; \hat y_{j}}\)

现在，我们结合上面的例子（单个样本 \(y = \begin{bmatrix} 0 & 1 & 0 & 0 \end{bmatrix}\)）来更好地理下解整个过程。在这个样本中 \(y_{1} =y_{3} = y_{4} = 0\)，只有 \(y_{2} =1\)，将其代入损失函数中求和之后，只剩下 \(-y_{2} \; {log} \; \hat y_{2}\)，因为所有 \(y_j\) 值为 0 时的项都为 0，又因为 \(y_{2}=1\)，所以最后 \(L\left( \hat y,y \right) = - \ log\hat y_{2}\)。

这就意味着，如果你的学习算法试图将它变小，因为梯度下降法是用来减少训练集的损失的，而要使它变小的唯一方式就是使 \(-{\log}\hat y_{2}\) 变小，要想做到这一点，就需要使 \(\hat y_{2}\) 尽可能大，因为它是概率，所以不可能比 1 大，但这的确也讲得通，因为在这个例子中 \(x\) 是猫的图片，你就需要这项输出的概率尽可能地大（\(\hat y = \begin{bmatrix} 0.3 & 0.2 & 0.1 & 0.4 \end{bmatrix}\) 中的第二个元素）。概括来讲，损失函数所做的就是它找到你的训练集中的真实类别，然后试图使该类别相应的概率尽可能地高，如果你熟悉统计学中 最大似然估计，这其实就是 最大似然估计的一种形式。

这是单个训练样本的损失，整个训练集的损失 \(J\) 就是对所有的单个训练样本的损失求总和。即：

\(J( w^{[1]},b^{[1]},\ldots\ldots) = \frac{1}{m}\sum\limits_{i = 1}^{m}{L( \hat y^{(i)},y^{(i)})}\)

因此你要做的就是用梯度下降算法来最小化 \(J\)。

最后，Softmax 输出层的导数为 ：\(dz^{[L]} = \frac{\partial J}{\partial z^{[L]}} = \hat{y} -y\)

有了 \(dz^{[L]}\) 之后，就可以开始反向传播的过程，计算整个神经网络中所需要的所有导数。

在这周的练习中，我们将开始使用一种深度学习编程框架，对于这些编程框架，通常你只需要专注于把前向传播做对，它自己会弄明白怎样反向传播，并帮你实现反向传播，但如果你想从头开始自己实现 Softmax 回归或者 Softmax 分类，那么这个表达式值得牢记（\(dz^{[L]} = \hat{y} -y\)），但在这周的练习中你不会用到它，因为编程框架会帮你搞定导数计算。Softmax 分类就讲到这里，有了它，你就可以运用学习算法将输入分成不止两类，而是 \(C\) 个不同类别。

Softmax 的 Python 实现代码：

# Apply exp() element-wise to x. Use np.exp(...).
x_exp = np.exp(x) # (n,m)

# Create a vector x_sum that sums each row of x_exp. 
# Use np.sum(..., axis = 1, keepdims = True).
x_sum = np.sum(x_exp, axis = 1, keepdims = True) # (n,1)
    
# Compute softmax(x) by dividing x_exp by x_sum. 
# It should automatically use numpy broadcasting.
s = x_exp / x_sum  # (n,m)

深度学习框架（Deep learning frameworks）

你已经差不多从零开始学习了使用 Python 和 NumPy 实现深度学习算法，很高兴你这样做了，因为我希望你理解这些深度学习算法实际上在做什么。但你会发现，如果应用更复杂的模型，例如卷积神经网络，或者循环神经网络，或者当你开始应用很大的模型，那么它就越来越不实用了，至少对大多数人而言，从零开始全部靠自己实现并不现实。

幸运的是，现在有很多好的深度学习软件框架，可以帮助你实现这些模型。想象一下，我猜你知道如何做矩阵乘法，你还知道如何编程实现两个矩阵相乘，但是当你在建很大的应用时，你很可能不想用自己的矩阵乘法函数，而是想要访问一个数值线性代数库，它会更高效，但如果你明白两个矩阵相乘是怎么回事还是挺有用的。我认为现在深度学习已经很成熟了，利用一些深度学习框架会更加实用，会使你的工作更加有效，那就让我们来看下有哪些框架，如下图：

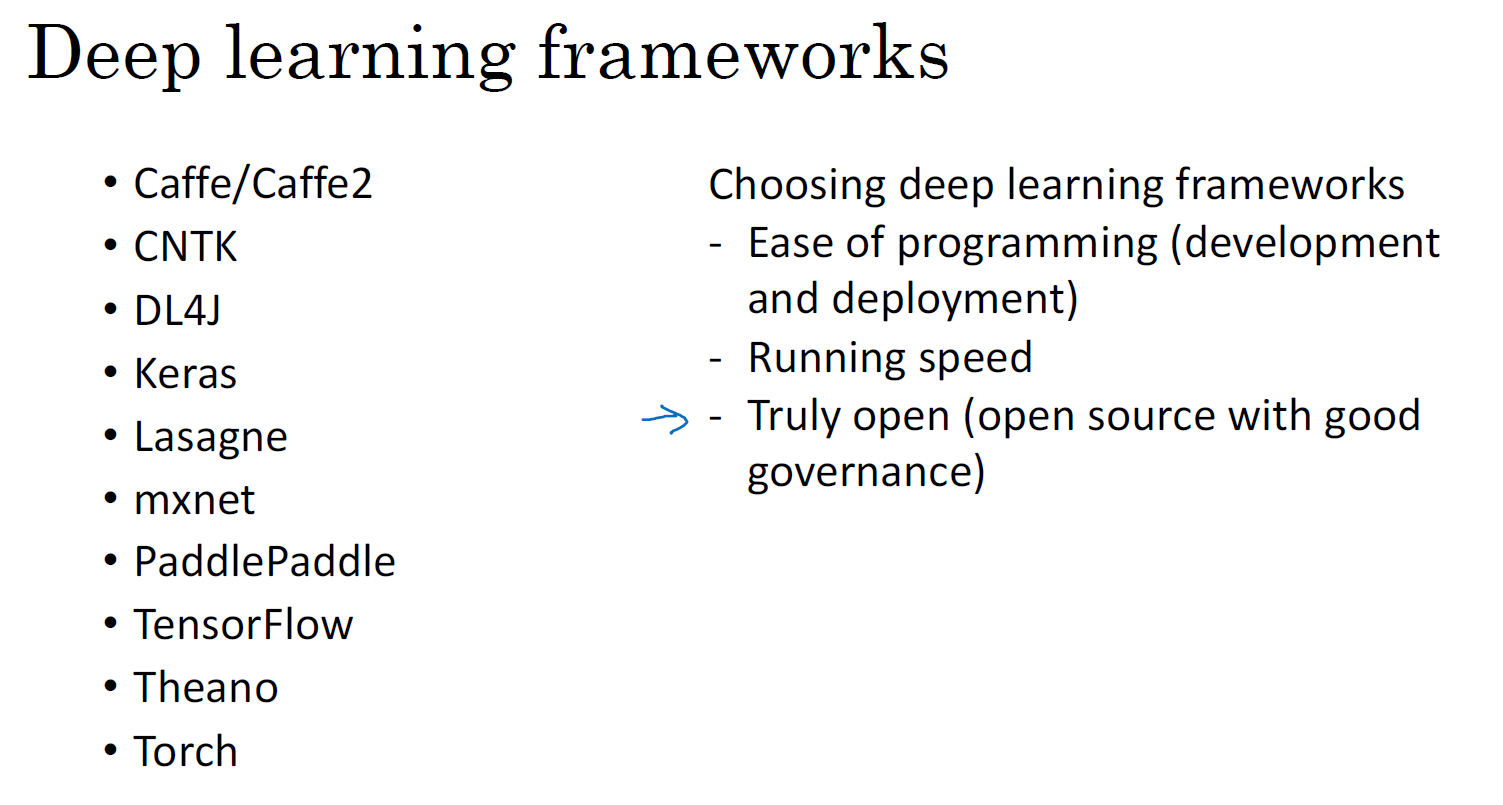
现在有许多深度学习框架，能让实现神经网络变得更简单，我们来讲主要的几个。每个框架都针对某一用户或开发群体的，我觉得这里的每一个框架都是某类应用的可靠选择，有很多人写文章比较这些深度学习框架，以及这些深度学习框架发展得有多好，而且因为这些框架往往不断进化，每个月都在进步，如果你想看看关于这些框架的优劣之处的讨论，你可以己去网上搜索，但我认为很多框架都在飞速的进步，越来越好，因此我不做强烈推荐，而是与你分享推荐一下选择框架的标准。

• 便于编程：这既包括神经网络的开发和迭代，还包括为产品进行配置，为了成千上百万，甚至上亿用户的实际使用，取决于你想要做什么。

• 运行速度：特别是训练大数据集时，一些框架能让你更高效地运行和训练神经网络。

• 框架是否真的开放：这个标准人们不常提到，但我觉得很重要，要是一个框架真的开放，它不仅需要开源，而且需要良好的管理。不幸的是，在软件行业中，一些公司有开源软件的历史，但是公司保持着对软件的全权控制，当几年时间过去，人们开始使用他们的软件时，一些公司开始逐渐关闭曾经开放的资源，或将功能转移到他们专营的云服务中。因此我会注意的一件事就是你能否相信这个框架能长时间保持开源，而不是在一家公司的控制之下，它未来有可能出于某种原因选择停止开源，即便现在这个软件是以开源的形式发布的。但至少在短期内，取决于你对语言的偏好，看你更喜欢 Python，Java 还是 C++ 或者其它什么，也取决于你在开发的应用，是 计算机视觉，还是 自然语言处理 或者 线上广告，等等，我认为这里的多个框架都是很好的选择。

程序框架就讲到这里，通过提供 比数值线性代数库更高程度的抽象化，这里的每一个程序框架都能让你在开发深度机器学习应用时更加高效。

TensorFlow

欢迎来到这周的最后一节课，有很多很棒的深度学习编程框架，其中一个是 TensorFlow，我很期待帮助你开始学习使用 TensorFlow，我想在这节课中向你展示 TensorFlow 程序的基本结构，然后让你自己练习，学习更多细节，并运用到本周的编程练习中，这周的编程练习需要花些时间来做，所以请务必留出一些空余时间。

先提一个启发性的问题，假设你有一个损失函数 \(J\) 需要最小化，在本例中，我将使用这个高度简化的损失函数，\(J(w)= w^{2}-10w+25\)，这就是损失函数，也许你已经注意到该函数其实就是 \({(w -5)}^{2}\)，如果你把这个二次方式子展开就得到了前面的表达式，所以使它最小的 \(w\) 值是5，但假设我们不知道这一点，你只有这个函数，我们来看一下怎样用 TensorFlow 将其最小化。当然，你也可以有一些更加复杂的损失函数 \(J(w,b)\)，这要取决于你的神经网络，然后你就能用 TensorFlow 自动找到使损失函数最小的 \(w\) 和 \(b\) 的值。但下面，让我们先从一个简单点的例子入手。

import numpy as np
import tensorflow as tf

# 声明 w 为 TensorFlow 变量
w = tf.Variable(0, dtype = tf.float32) 

# 使用 add 和 multiply 函数定义 cost
cost = tf.add(tf.add(w ** 2, tf.multiply(- 10., w)), 25) 

# 如果要是觉得上面定义 cost 的写法不好看，可以使用 TensorFlow 重载后的一般的加减运算。
# 一旦 w 被声明为 TensorFlow 变量，平方，乘法和加减运算都被重载了，因此你不必使用上面这种不好看的句法。
# 因此你也可以把 cost 写成更好看的形式，重新运行，会得到同样结果。
cost = w ** 2 - 10 * w + 25

# 定义学习算法用于训练（梯度下降），其中学习率 0.01， 目标最小化 cost
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

init = tf.global_variables_initializer()

## 符合表达习惯的写法
session = tf.Session() # 开启一个 TensorFlow session
session.run(init) # 初始化全局变量。
print (session.run(w)) # 让 TensorFlow 评估一个变量

# 如果运行上面的 session.run(w) ，它评估 w 等于0，因为到目前为止程序还没有运行过梯度下降

# 下面运行一步梯度下降，再查看 w 的值，应该变成 0.1
session.run(train)
print (session.run(w))

# 接着我们运行梯度下降1000次迭代，再查看 w 的值，应该变成 4.99999
# 因为 w 的最优值是 5，所以这个结果已经很接近了
for i in range(1000):
    session.run(train)
print (session.run(w))

# 有些程序员会用这种 with 的句式，作用基本上与上面的 session 代码是一样的。
# 但是 Python 中的 with 命令更方便清理，以防在执行这个内循环时出现错误或例外。
# 默认执行完 with 包含的语句之后，程序会自动调用清理的方法
with tf.Session() as session:
    session.run(init)
    session.run(train)
    print (session.run(w))

# 本例中 cost 的系数已经固定（即：1，-20，25），这个系数相当于一个训练样本
# 下面演示在 TensorFlow 中如何将训练数据传入 cost 中并训练
# 先定义一个 x，让它扮演训练数据的角色，事实上训练数据有 x 和 y，但这个例子中只有 x

# x 是 (3, 1) 维的数组
# placeholder 函数告诉 TensorFlow，稍后会为 x 提供数值
x = tf.placeholder(tf.float32, [3,1])

# x (系数数组) 变成可以控制这个二次函数系数的数据
cost = x[0][0] * w**2 + x[1][0] * w + x[2][0]

# 再定义一个数组，这就是我们将要喂给 x 的数据
coefficients = np.array([[1], [-20], [25]])

# 最后我们需要用某种方式把这个系数数组接入变量 x
# 能做到这一点的句法是 feed_dict = {x : coefficients}
# 运行梯度下降 1 次迭代
with tf.Session() as session:
    session.run(init)
    session.run(train, feed_dict = {x : coefficients})
    print (session.run(w))

# 运行梯度下降 1000 次迭代
with tf.Session() as session:
    session.run(init)
    for i in range(1000):    
        session.run(train, feed_dict = {x : coefficients})
    print (session.run(w))

# 我们试着改变下这个二次函数的系数
# cost 将变成 (w - 10)^2,  上面例子中是 (w - 5)^2
coefficients = np.array([[1.],[-20.],[100.]])

# 运行梯度下降 1 次迭代，结果大约是 0.2
with tf.Session() as session:
    session.run(init)
    session.run(train, feed_dict = {x : coefficients})
    print (session.run(w))

# 运行梯度下降 1000 次迭代， 结果大约是 9.99998
with tf.Session() as session:
    session.run(init)
    for i in range(1000):    
        session.run(train, feed_dict = {x : coefficients})
    print (session.run(w))

# 在做 mini-batch 梯度下降的每一次迭代时，需要插入不同的 mini-batch
# 那么每一次迭代，就可以使用 feed_dict 来喂入训练集的不同子集
# 把不同的 mini-batch 喂入损失函数需要数据的地方

让 TensorFlow 如此强大的是，你只需说明如何计算损失函数，它就能求导，而且用一两行代码就能运用梯度优化器，Adam 优化器或者其他优化器。

cost =x[0][0]*w**2 +x[1][0]*w + x[2][0]

TensorFlow 程序的核心是计算损失函数，然后 TensorFlow 自动计算出导数，以及如何最小化损失，因此上面的这个等式或者说这行代码，它所做的就是让 TensorFlow 建立计算图，计算图所做的就是取 \(x[0][0]\)，取 \(w\)，然后将 \(w\) 平方，然后 \(x[0][0]\) 和\(w^{2}\) 相乘，你就得到了 \(x[0][0]*w^{2}\)，以此类推，最终整个建立起来计算 \(cost = x[0][0]*w**2 + x[1][0]*w + x[2][0]\)，最后，得到最终的损失函数值。

TensorFlow 的优点在于，通过计算 cost，计算图就基本实现了前向传播，而像 TensorFlow 之类的编程框架已经内置了必要的反向函数，这也是为什么通过内置函数来计算前向传播，它也能自动用反向函数来实现反向传播，即便函数非常复杂，它也可以帮你计算出导数，这就是为什么你不需要明确实的现反向传播，这也是编程框架能帮你变得高效的原因之一。

另外，如果你看 TensorFlow 的使用说明，你会发现它的计算图的符号和我的有些不同，它用了 \(x[0][0]​\)，\(w​\)，然后在图的节点上，它不是写出值，像是的 \(w^{2}​\) 或 \(x[0][0]*w^{2}\)，TensorFlow 使用说明倾向于只写运算符，所以它会在节点中只显示平方运算的符号（而不是 \(w^{2}​\)），然后这两者再一起共同指向一个乘法运算符号（而不是我们这种表示方式 \(x[0][0]*w^{2}\)），以此类推，然后在最后的节点，我猜应该是一个将 \(x[2][0]​\) 加上去得到最终值的加法运算符号。

为本课程起见，我认为计算图节点使用显示值的方式会更容易理解，但是如果你去看 TensorFlow 使用说明中的计算图，会有另一种表示方式，节点都是用运算符号来标记的，而不是值，但这两种呈现方式表达的是同样的计算图。

在编程框架中你可以用一行代码做很多事情，例如，你不想用梯度下降法，而是想用 Adam 优化器，你只要改变这行代码，就能很快换掉它，换成更好的优化算法。所有现代深度学习编程框架都支持这样的功能，让你很容易就能编写复杂的神经网络。