[C10] 异常检测(Anomaly Detection)
异常检测(Anomaly Detection)
问题的动机 (Problem Motivation)
异常检测(Anomaly detection)问题是机器学习算法中的一个常见应用。这种算法的有趣之处在于:它虽然主要用于非监督学习问题,但从某些角度看,它又和监督学习问题非常类似。
举例说明什么是异常检测:
假想你是一个飞机引擎制造商,当你生产的飞机引擎从生产线上流出时,你需要进行QA(质量控制测试),而作为这个测试的一部分,你测量了飞机引擎的一些特征变量,比如引擎运转时产生的热量,或者引擎的振动等。如果你生产了 \(m\) 个引擎的话,那么你就有了一个数据集,从 \(x^{(1)}\) 到 \(x^{(m)}\),将这些数据绘制成图表,如下图中红色X所示。这里每个叉,都是无标签的数据。那么 ,异常检测问题可以定义为:我们假设后来有一天,你有一个新的飞机引擎从生产线上流出,而你的新飞机引擎有特征变量 \(x_{test}\),我们希望知道这个新的飞机引擎是否有某种异常,或者说,我们希望判断这个引擎是否需要进一步测试。因为,如果它看起来像一个正常的引擎,那么我们可以直接将它运送到客户那里,而不需要进一步的测试。从直觉上先来理解下异常检测问题,现在假设,这个新的飞机引擎,如下图,它出现在比较靠近中心的位置(绿X),那么它看起来是 OK 的,但如果它出现的位置距离数据集的中心比较偏远,那么它有可能是 anomaly,我们可能需要对它再进行测试一下。
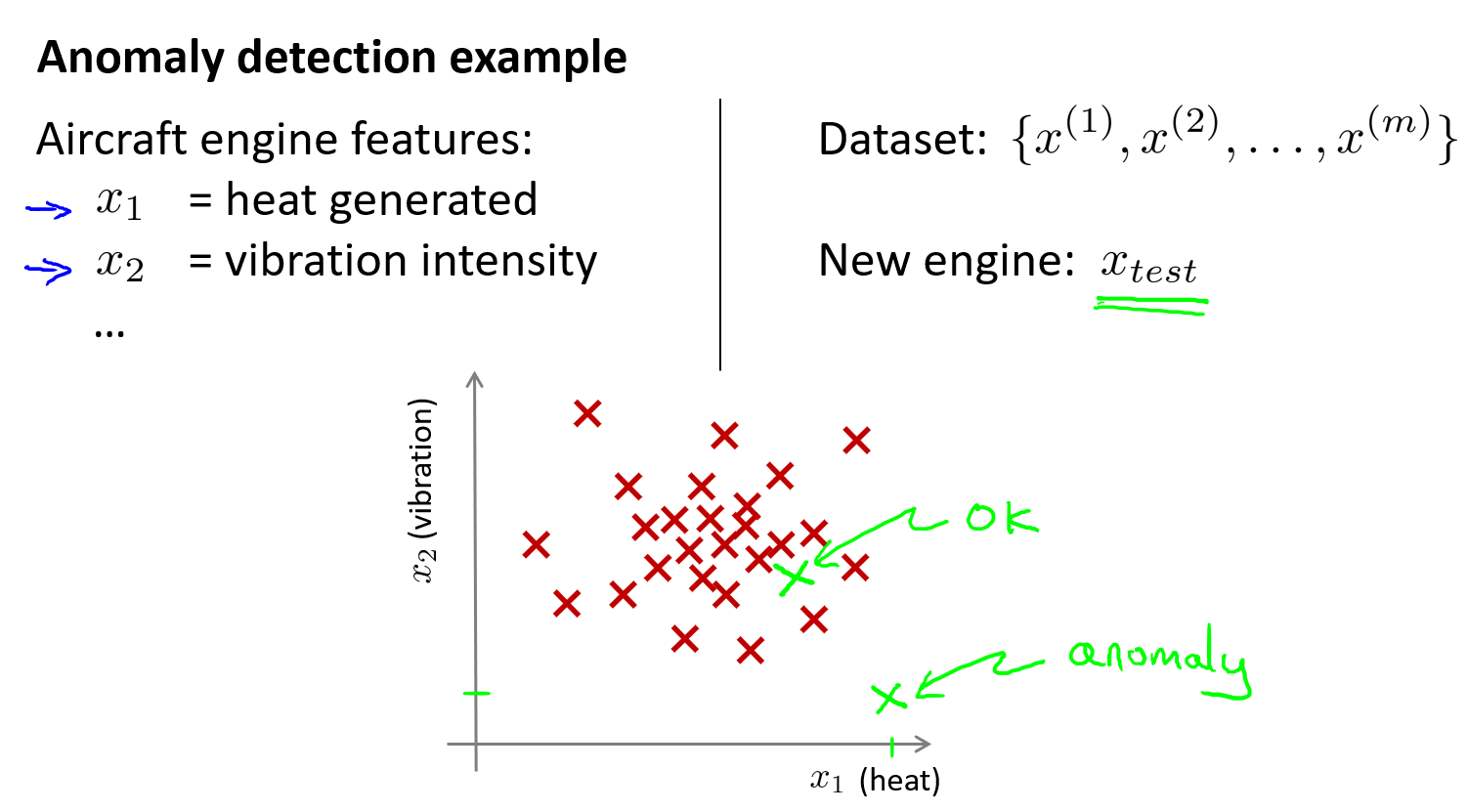
让我们稍微正式一点的来定义下这个问题:
假设我们有数据集 \(x^{(1)},x^{(2)},..,x^{(m)}\),通常我们假定 m 个样本都是正常的,然后我们希望有一个算法告诉我们,一个新的样本数据 \(x_{test}\) 是否异常,我们要采取的做法是,给定无标签的训练集,我们将对数据建模,即 \(p(x)\),也就是说,我们将对 \(x\) 的概率分布建模,其中 \(x\) 是这些特征变量,如引擎运转时产生的热量,或者引擎的振动等。因此,当我们建立了 \(x\) 的概率模型之后,我们就有对于一个新的飞机引擎 \(x_{test}\),它的概率 \(p(x_test)\) 如果低于一个阈值 \(\varepsilon\),那么就将其标记为异常(anomaly)。这意味着,对于整个数据集,这个点出现的概率非常的低。反之,如果概率大于等于给定的阈值 \(\varepsilon\),我们就认为它是正常的(normal)。这种方法称为密度估计,可表示为:\(if \quad p(x_{test}) \begin{cases} < \varepsilon & Anomaly \\ \geq \varepsilon & Normal \end{cases}\)
如下图,给定图中这样的训练集,如果你建立了一个模型,你将很可能发现飞机引擎,即模型 \(p(x)\) 会认为在中心区域的这些点概率相当大,而稍微远离中心区域的点概率会小点,更远地方的点,概率会更小,而在蓝色圈外面的点,将成为异常点。
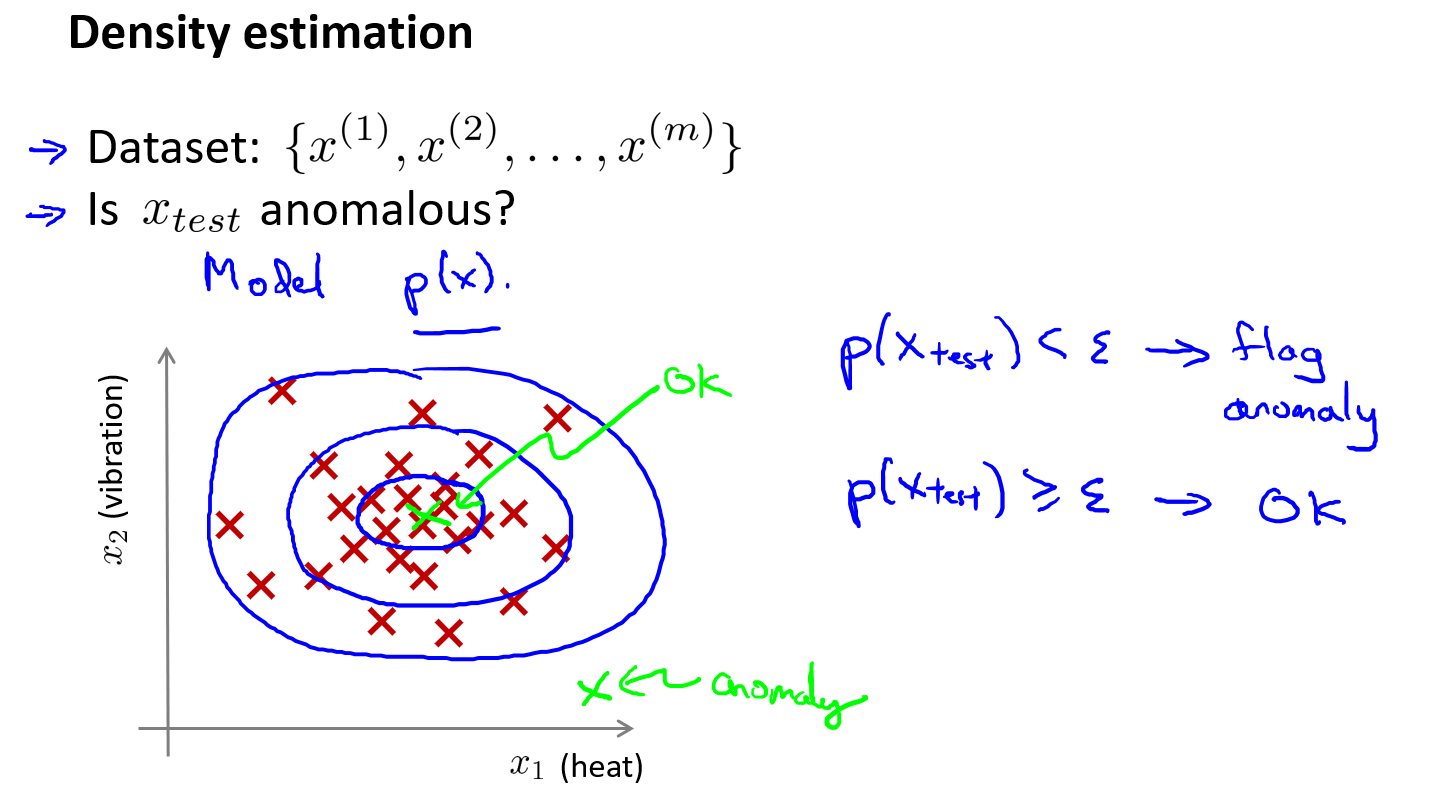
异常检测算法常用的应用案例:
-
欺诈检测(Fraud detection):如在线采集有关用户的特征数据,可能包含:用户多久登录一次,访问过的页面,在论坛发布的帖子数量,甚至是打字速度等。尝试根据这些特征构建一个模型,可以用这个模型来识别那些不符合该模式的用户。
-
制造业(Manufaturing):如上面介绍的飞机引擎的例子。
-
检测数据中心的计算机(Monitoring computer in a data center):特征可能包含:内存使用情况,被访问的磁盘数量,CPU 负载,网络的通信量等。根据这些特征可以构建一个模型,用来判断某些计算机是不是有可能出错了。
高斯分布 (Gaussian Distribution)
高斯分布,也称为正态分布(Normal Distribution )
Say \(x \in \mathbb{R}\). If \(x\) is a distributed as Gaussian with mean \(\mu\), variance \(\sigma^2\).
那么可以记作:\(x \sim N(\mu, \sigma^2)\),其中:
- \(\sim\) 表示服从什么什么的分布
- N 表示高斯分布,Normal的首字母
- \(\mu\) 是平均值
- \(\sigma^2\) 是方差,如果开方后,变成 \(\sigma\),就是标准差
如果我们将高斯分布的概率密度函数绘制出来,它看起来将会是一个钟形的曲线(如下图),它有两个参数,一个是 \(\mu\) ,它控制这个钟形曲线的中心位置,\(\sigma\) 控制这个钟形曲线的宽度,因此 \(\sigma\) 也被记作一个标准差,这条钟形曲线决定了 \(x\) 取不同值时的概率,在中心位置概率很大,两边的概率越来越小。
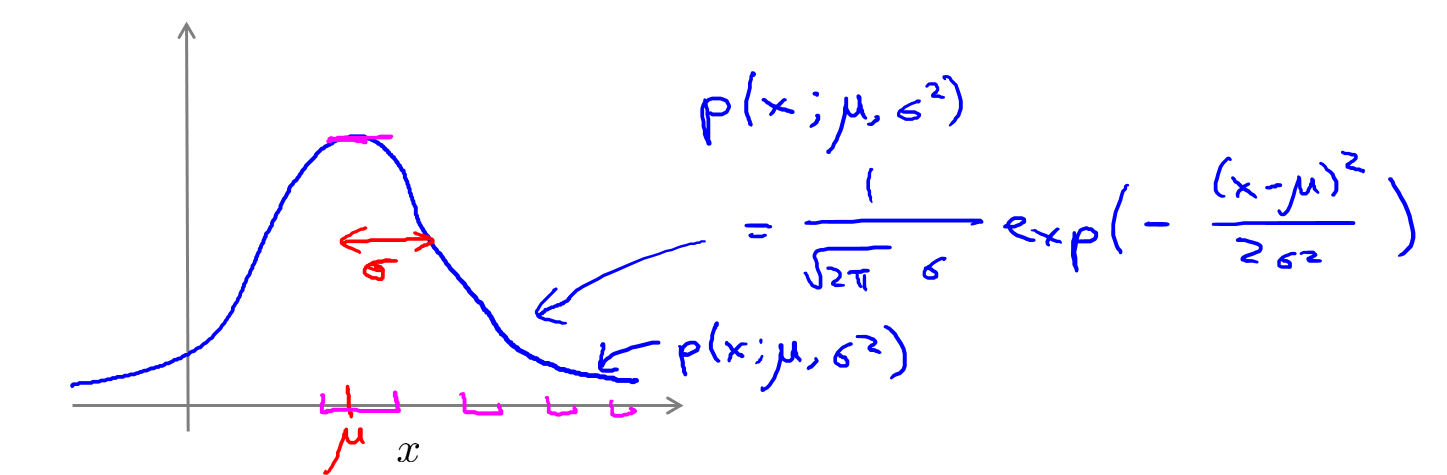
如果变量 \(x\) 服从高斯分布,即: \(x \sim N(\mu, \sigma^2)\),则其概率密度函数为:
\(p(x,\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\)
来看几个高斯分布的例子:
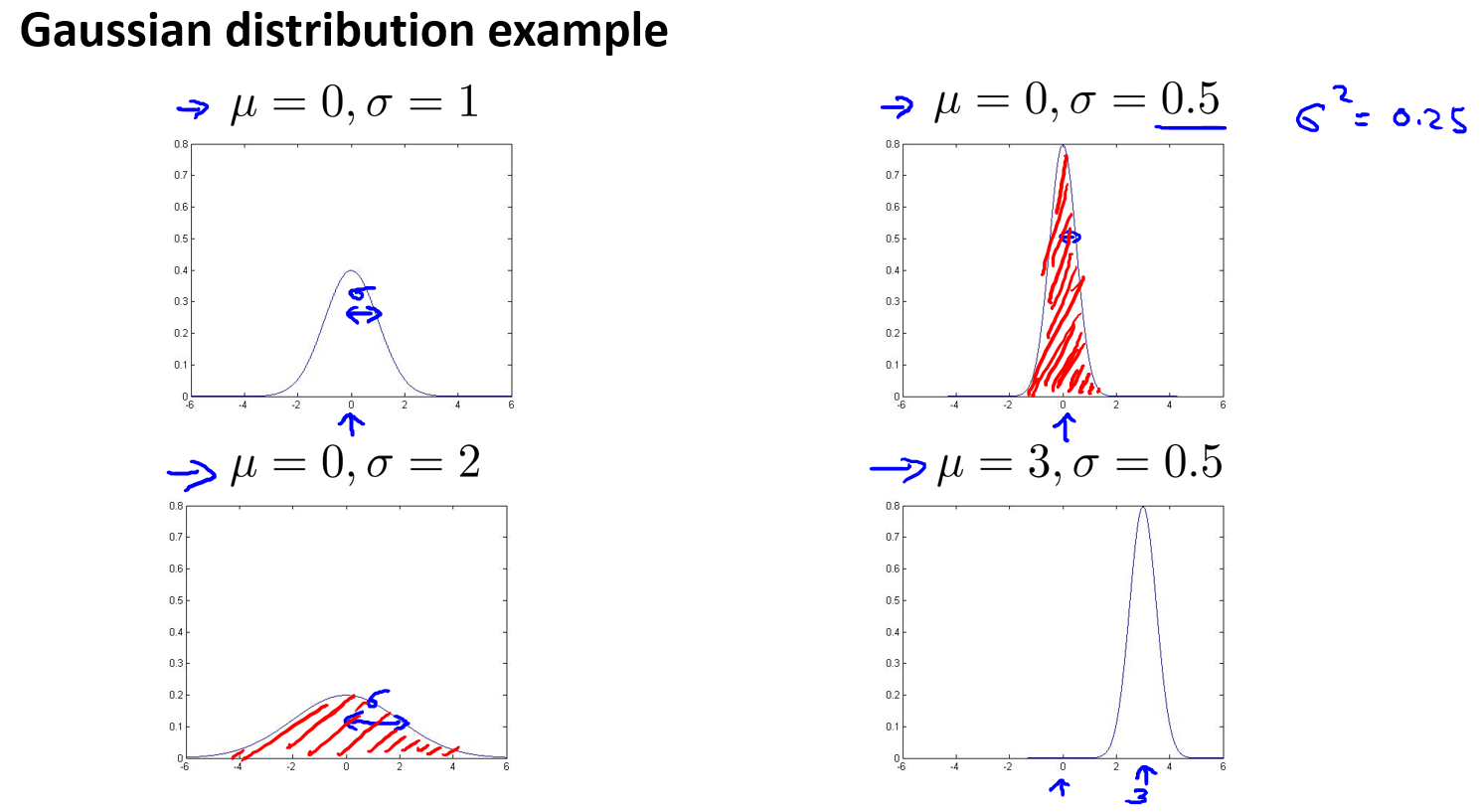
上图中,\(\mu\) 决定了曲线的中心点位置,而\(\sigma\),也就是一个标准差,决定了曲线的宽度。高斯分布概率密度曲线下方的阴影面积,积分一定为 \(1\),所以如果改变了 \(\sigma\) 的值,为了保证下方阴影面积不变,那么曲线的高度就会发生变化。
关于参数估计的问题(the parameter estimation problem):
参数估计问题就是给定数据集之后来估计参数 \(\mu\) 和 \(\sigma^2\),其实就是对 \(\mu\) 和 \(\sigma^2\) 的极大似然估计。
利用已有数据预测总体中的 \(\mu\) 和 \(\sigma^2\),公式如下:
\(\mu=\frac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}\)
\(\sigma^2=\frac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu)^2\)
注:对于上面求 \(\sigma^2\) 的公式,在统计学中会采用 \(\frac{1}{m-1}\),但在机器学习领域,人们更喜欢使用 \(\frac{1}{m}\)的版本,实际使用中两者差别很小。只要你有一个还算大的训练集,那么在机器学习领域大部分人更习惯使用 \(\frac{1}{m}\) 这个版本的公式。这两个版本的公式在理论特性和数学特性上稍有不同,但在实践中,它们区别很小。
另外一个需要注意的是,\(\mu\) 和 \(\sigma^2\) 的维度应该是 \(1 \times n\) 维的,这意味着,对于一个数据集,有 \(m\) 个样本,每个样本有 \(n\) 个特征,所以最终你会得到 \(n\) 个高斯分布,下一章节【算法】会详细说明。
算法(Algorithm)
密度估计(Density estimation)
Say :
- Training set : \({x^{(1)},...,x^{(m)}}\)
- Each example is \(x \in \mathbb{R}^n\),并且:
\(x_1 \sim N(\mu_1, \sigma_1^2)\)
\(x_2 \sim N(\mu_2, \sigma_2^2)\)
\(x_3 \sim N(\mu_3, \sigma_3^2)\)
...
\(x_n \sim N(\mu_n, \sigma_n^2)\)
我们处理异常检测的方法是,用数据集建立其概率模型 \(p(x)\),并试图计算出哪些特征量出现的概率比较高,哪些特变量出现的概率比较低。所以,对于样本 \(x\) 来说,有 \(n\) 个特征,先计算每个特征出现的概率,然后再将 \(n\) 个特征的出现概率累乘起来,那么这就是这整个样本的出现概率。据此,我们来建立模型 \(p(x)\):
\(\begin{align} p(x) = & p(x_1;\mu_1,\sigma_1^2)p(x_2;\mu_2,\sigma_2^2)...p(x_n;\mu_n,\sigma_n^2) \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \\ = & \prod\limits_{j=1}^np(x_j;\mu_j,\sigma_j^2) \\ = & \prod\limits_{j=1}^n\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2} {2\sigma_j^2}) \end{align}\)
上面的等式实际上等同于一个 \(x_1,x_2,...,x_n\) 上的独立假设(independence assumptions),不过在实践结果中表明,我要介绍的这个算法,它的效果不错,无论这些特征量是否近乎独立,并且即使这个独立假设不成立,这个算法也能正常运行。
Anomaly detection algorithm
- Choose features \(x_i\) that you think might be indicative of anomalous examples.
- Fit parameters \(\mu_1,...,\mu_n,\sigma_1^2,...,\sigma_n^2\)
\(\mu_j=\frac{1}{m}\sum\limits_{i=1}^{m}x_j^{(i)}\)
\(\sigma_j^2=\frac{1}{m}\sum\limits_{i=1}^{m}(x_j^{(i)}-\mu_j)^2\) - Given new example \(x\), compute \(p(x)\):
\(p(x) = \prod\limits_{j=1}^n\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2} {2\sigma_j^2})\)
Anomaly if \(p(x) < \varepsilon\)
Anomaly detection example
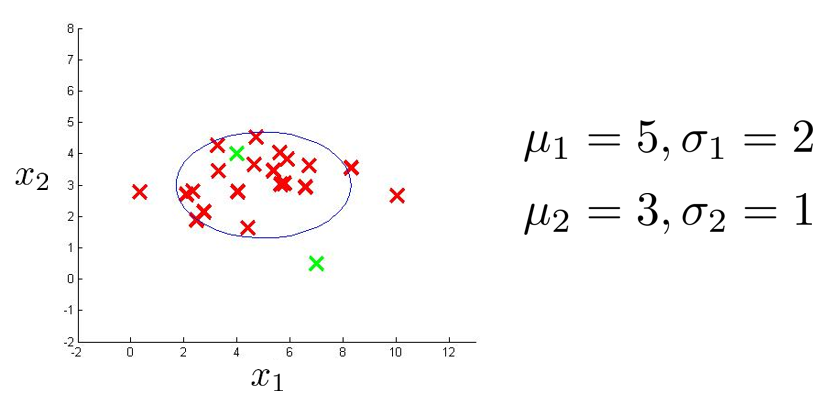
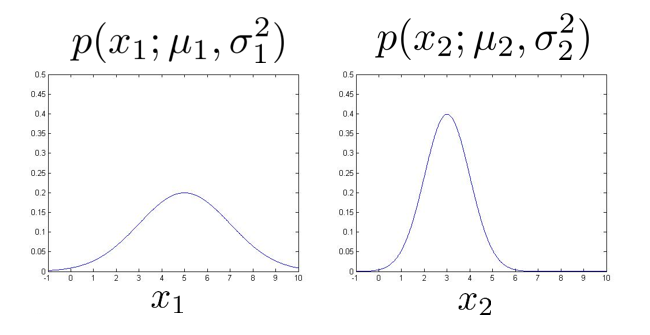
如上图,假定数据集有两个特征 \(x_1,x_2\),并且已经分别计算出了每个特征的 \(\mu\) 和 \(\sigma^2\),现在分别画出每个特征的概率分布图:
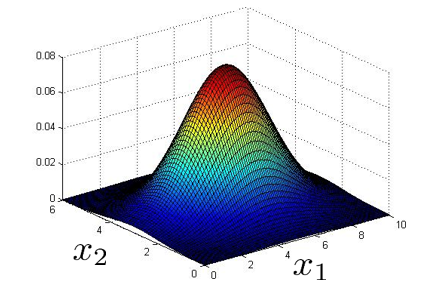
然后将两个特征的概率相乘,会得到下面三维(合并后的)的概率分布图:
现在,设定一个阈值,令:\(\varepsilon= 0.02\)
然后计算两个新样本(\(x_{test}^{(1)},x_{test}^{(2)}\))的概率,即:上图中的两个绿色 X:
\(p(x_{test}^{(1)}) = 0.0426 \geq \varepsilon\),标记为异常点
\(p(x_{test}^{(2)}) = 0.0021 < \varepsilon\),标记正常
开发和评价一个异常检测系统(Developing and Evaluating an Anomaly Detection System)
异常检测算法是一个非监督学习算法,意味着我们无法根据结果变量 \(y\) 的值来告诉我们数据是否真的是异常的。所以,可以从带标记(异常或正常)的数据着手,从其中选择一部分正常数据用于构建训练集,然后用剩下的正常数据和异常数据混合的数据构成交叉检验集和测试集,最后,由于交叉验证集和测试集中的正负样本数量是非常倾斜的,所以我们选择用 \(F1\) 值来评估算法。
下面举例说明:
Say :我们有10000台正常引擎的数据,有20台异常引擎的数据,分配数据如下:
- 6000台正常引擎的数据作为训练集
- 2000台正常引擎 和 10台异常引擎的数据作为交叉检验集
- 2000台正常引擎 和 10台异常引擎的数据作为测试集
具体评估方法如下:
- 根据训练集数据,估计 \(\mu\) 和 \(\sigma^2\),并构建概率模型 \(p(x)\)
- 在交叉检验集尝试使用不同的 \(\varepsilon\) 作为阀值进行预测,选择令 \(F1\) 值最大的 \(\varepsilon\)
- 在测试集再次进行预测,计算 \(F1\) 值,评估算法的泛化能力
异常检测与监督学习对比(Anomaly Detection vs. Supervised Learning)
异常检测算法中,我们也使用了带有标签的数据,那为什么不使用监督学习算法呢?
- 对于异常检测算法,可以理解为一种排除算法,让它学习大量的 Normal 样本,它就可以通过排除的方式找出所有有异常(包括多种多样的、已知的、未知的异常类型,因为只要不是Normal那它就是异常)的样本。
- 对于监督学习算法,必须让算法充分的学习到所有已知类型的样本,而且最好不同类别的训练样本数量上是均衡的,它才能更好的区分不同的类型。
选择特征(Choosing What Features to Use)
预处理 Non-gaussian features
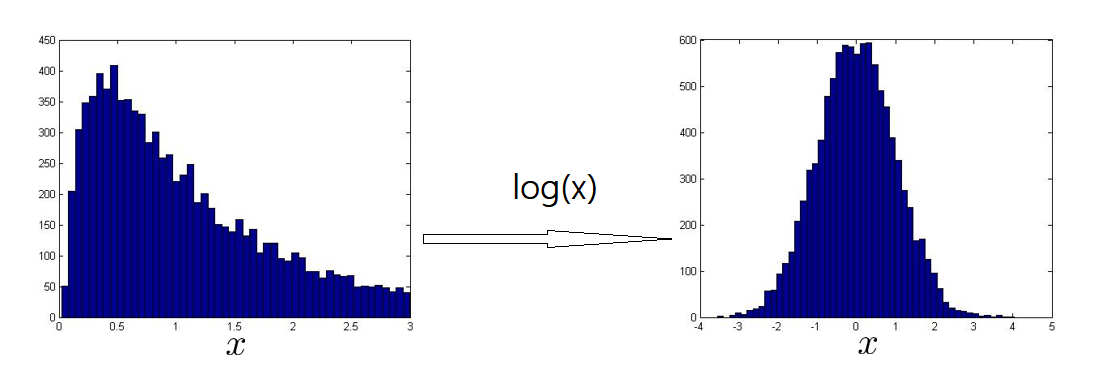
异常检测假设特征符合高斯分布,如果数据的分布不是高斯分布,异常检测算法也能够工作,但是最好还是将数据转换成高斯分布,例如使用对数函数:\(x= log(x+c)\),其中 \(c\) 为非负常数; 或者 \(x=x^c\),\(c\) 为 0-1 之间的一个分数。如下图,用直方图的方式画出一个特征,并使用 log(x) 来改变,使该特征符合高斯分布。
Error analysis for anomaly detection
Want :
- \(p(x)\) large for normal examples \(x\)
- \(p(x)\) small for anomalous examples \(x\)
Most common problem:
- \(p(x)\) is comparable (say, both large) for normal and anomalous examples. 异常的数据有较高的 \(p(x)\) 值,因而被算法认为是正常的。这种情况下误差分析能够帮助我们,可以分析那些被算法错误预测为正常的数据,观察能否找出一些问题,或是给我们一些启发,让我们增加一些新的特征,从而让算法更好地工作。
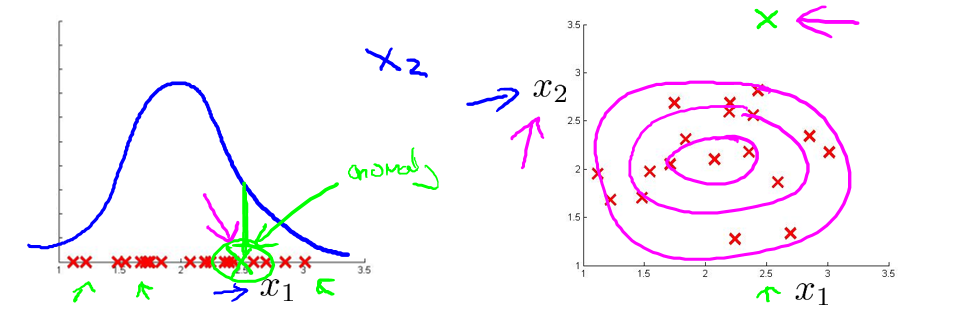
上图左,一个异常的样本被正常的样本淹没了,它只有一个特征 \(x_1\)
上图右,为样本添加一个新特征 \(x_2\),让它的值略微大一些(图中大概3.5的位置),如此就可以把它正确的划分到阈值外面了
分享一下我(Andrew Ng)平时在异常检测算法选择特征变量时的一些思考
正常情况下,I'll choose features that might take on unusually large or small values in the event of an anomaly.
举 一个 Monitoring computers in a data center 的例子, say :
- \(x_1\) = memory use of computer
- \(x_2\) = number of disk accesses/sec
- \(x_3\) = CPU load
- \(x_4\) = network traffic
正常情况下,CPU load 和 network traffic 是呈线性关系的。那么假设现在我们想捕捉一种新的异常情况,如,某个程序进入了死循环,所以 CPU load 很高,但是 network traffic 还是正常的。所以我设计了一个新特征 \(x_5 = \frac{\text{CPU load}}{\text{network traffic}}\),如果发生这种异常,此时 \(x_5\) 的值会变得非常大,就会被算法捕捉到。或者类似的新特征 \(x_6 = \frac{(\text{CPU load})^2}{\text{network traffic}}\),看上去像是 \(x_5\) 的一个变体,但它也同样可以让算法帮我们捕捉到这种有很高的 CPU 负载,但是网络流量又很低的情况。
多元高斯分布 - Multivariate Gaussian(Normal) distribution - Optional
目前为止学习的异常检测算法存在一种扩展,这个扩展会用到多元高斯分布,它有一些优势,也有一些劣势,它能捕捉到之前算法检测不出来的异常
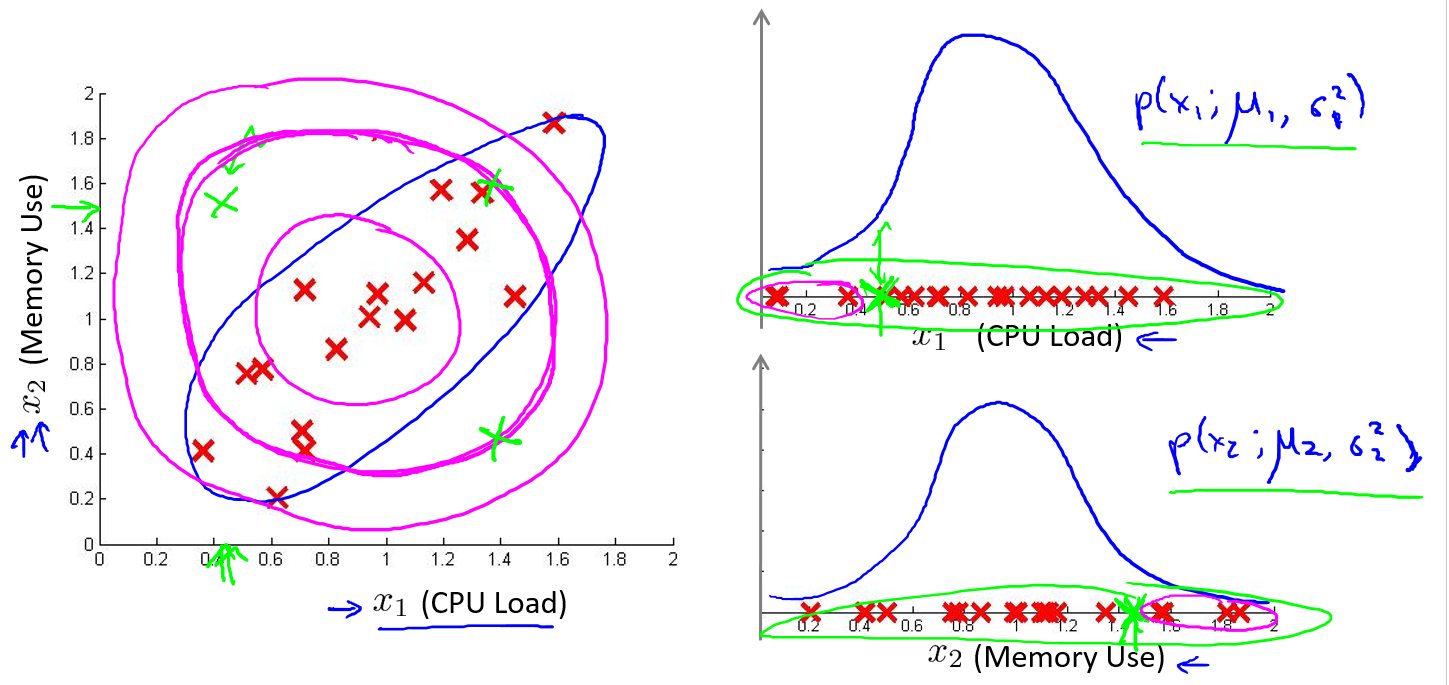
举例说明,如上图所示,给定一个监控中心例子的数据集, \(x_1\) 是 CPU 负载,\(x_2\) 是内存使用率,可以看出它们俩个是线性相关的(CPU 增大,内存也增大)。现在给出一个新的样本,坐标(0.5, 1.5)位置的绿色 X,从直觉来看,样本都聚集在了蓝色圈内,这个新的样本应该属于异常点。我们在右边的图中分别画出这个新样本两个特征的高斯分布图,可以看到它们的概率都很高,它们的乘积,也就是 \(p(x)\) 也很高,所以用之前的高斯分布算法,这个新样本不会被识别为异常点,它的识别范围如左边图中洋红色圈圈所示。为此,可对现有的高斯分布算法进行扩展,使用多元高斯分布,那么算法将会使用蓝色的圈来拟合样本的概率。换句话说,多元高斯分布可以拟合出一种正相关或者是负相关的概率分布图形来,本例是正的线性相关。
多元高斯分布(多元正态分布),下面是具体做法:
\(x \in \mathbb{R}^n\). Don't model \(p(x_1),p(x_2),...,\)etc. separately. 不要分别为 \(p(x_1),p(x_2),...,\)etc. 建模
Model \(p(x)\) all in one go. 而要建立一个整体的 \(p(x)\) 模型。
Parameters : \(\mu \in \mathbb{R}^n, \Sigma \in \mathbb{R}^{n \times n}\)(covariance matrix)
先来回顾下之前学到的高斯分布模型,可以看到它计算 \(p(x)\) 的方法是通过分别计算每个特征对应的概率,然后将其累乘,最终得到 \(p(x)\) :
\(\mu_j=\frac{1}{m}\sum\limits_{i=1}^{m}x_j^{(i)}\)
\(\sigma_j^2=\frac{1}{m}\sum\limits_{i=1}^{m}(x_j^{(i)}-\mu_j)^2\)
\(p(x) = \prod\limits_{j=1}^n p(x; \mu_j, \sigma_j^2) = \prod\limits_{j=1}^n\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2} {2\sigma_j^2})\)
在多元高斯分布模型中,我们将构建特征的协方差矩阵,用所有的特征一起来计算 \(p(x)\):
\(\mu=\frac{1}{m}\sum\limits_{i=1}^mx^{(i)}\)
\(\Sigma = \frac{1}{m}\sum\limits_{i=1}^m(x^{(i)}-\mu)(x^{(i)}-\mu)^T=\frac{1}{m}(X-\mu)^T(X-\mu)\)
\(p(x;\mu,\sigma)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp\Big(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\Big)\)
其中:
- \(|\Sigma|\) 是对 \(\Sigma\) 求行列式(determinant)
- \(\Sigma^{-1}\) 是求 \(\Sigma\) 的逆矩阵
- \(\Sigma\) 是协方差矩阵,在之前的高斯分布模型中,我们会为每个特征计算出方差 \(\sigma^2\),而在多元高斯分布模型中,之前的方差 \(\sigma^2\) 全部对应到了这个协方差矩阵的正对角线上。
换言之,如果多元高斯分布模型中的协方差矩阵只有正对角线上有值,其他地方全部为 0 的话 ,那就意味着和之前的高斯分布模型是一样的。而除了正对角线以外的地方如果也有值,就会产生一些正相关和负相关的效果。
下面我们来看看协方差矩阵是如何影响模型的:
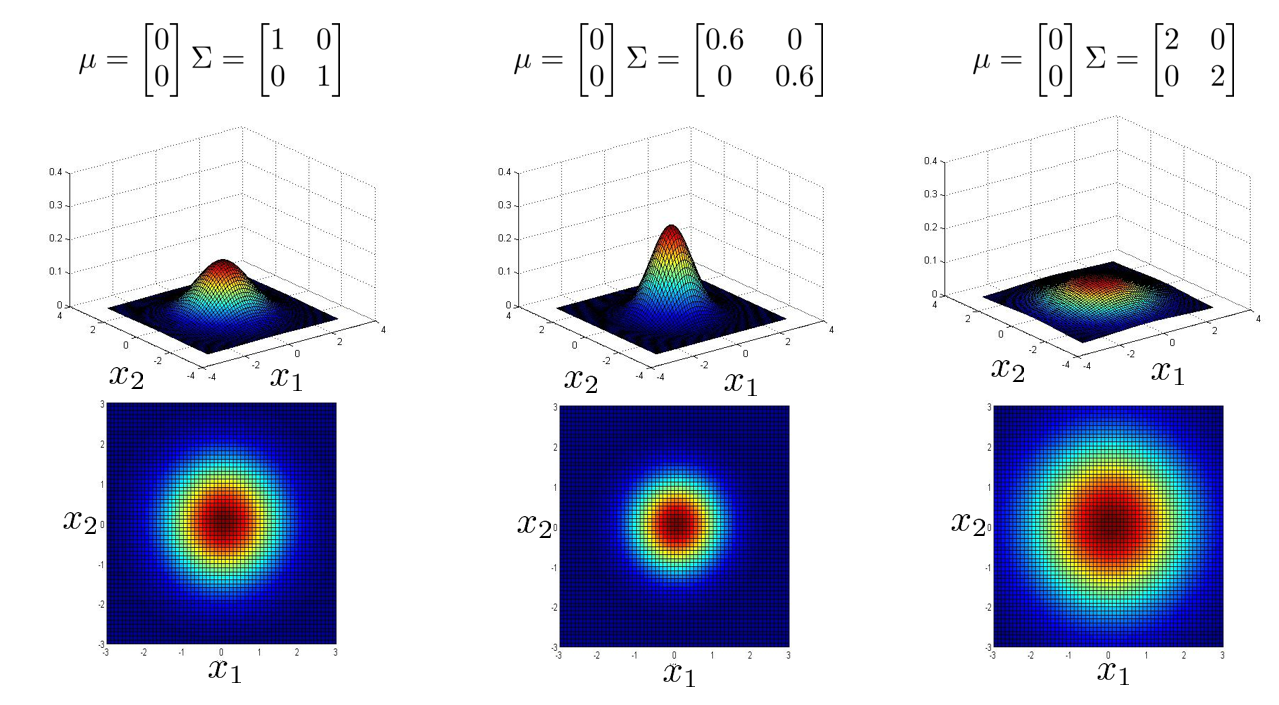
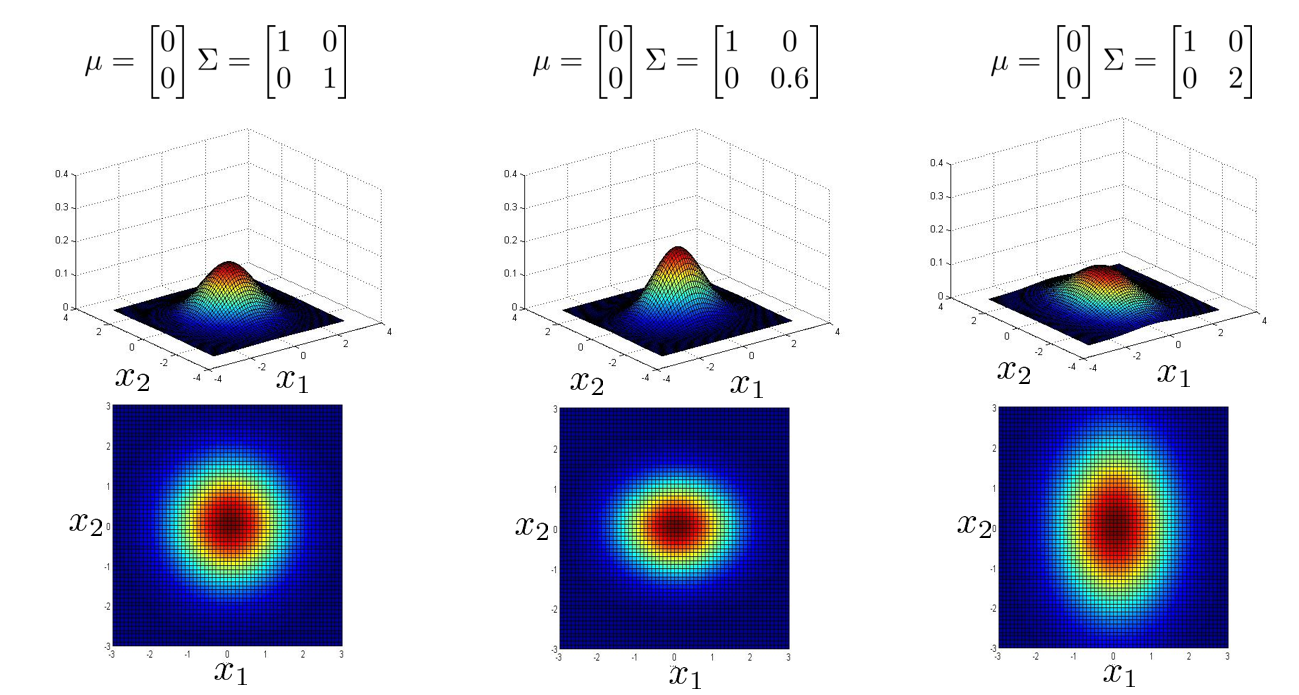
下面三张图中,协方差矩阵 \(\Sigma\) 中只有正对角线有非 0 值,说明虽然它是用多元高斯分布的方法来计算,但是它能捕获的概率图形和之前学的普通高斯分布效果一样。可以看到普通高斯分布的概率图形都是圆形或是椭圆的,而且都是轴对称的。
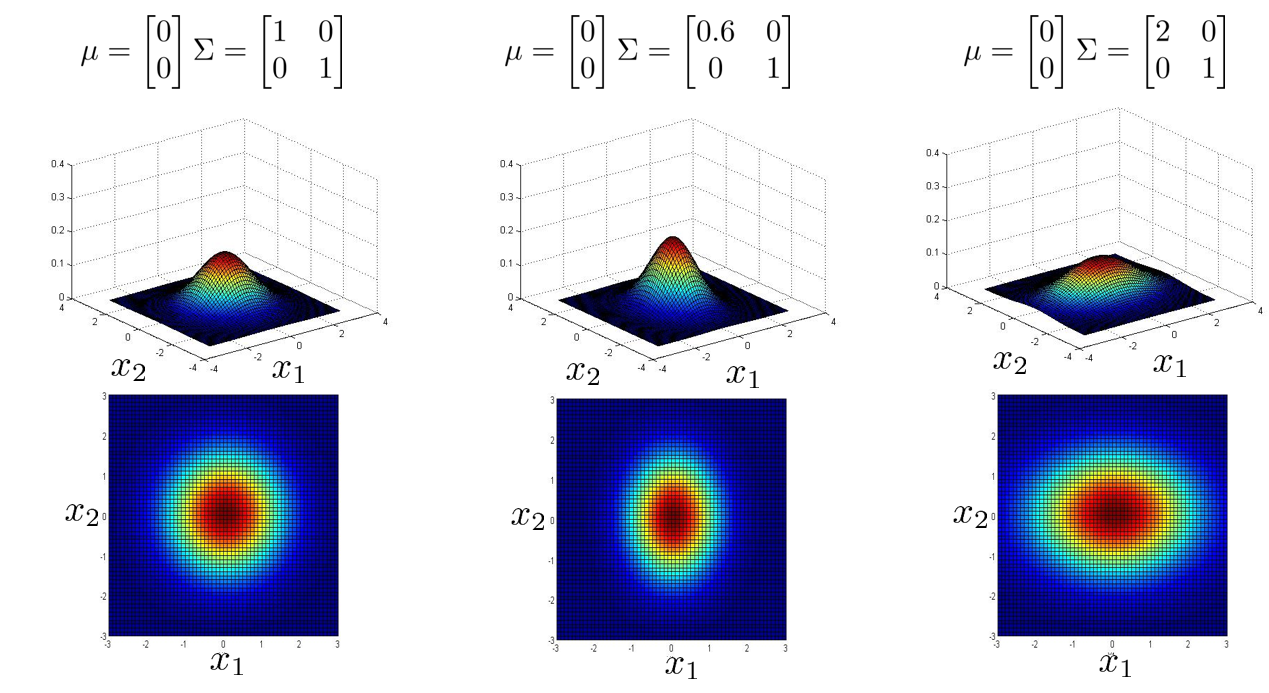
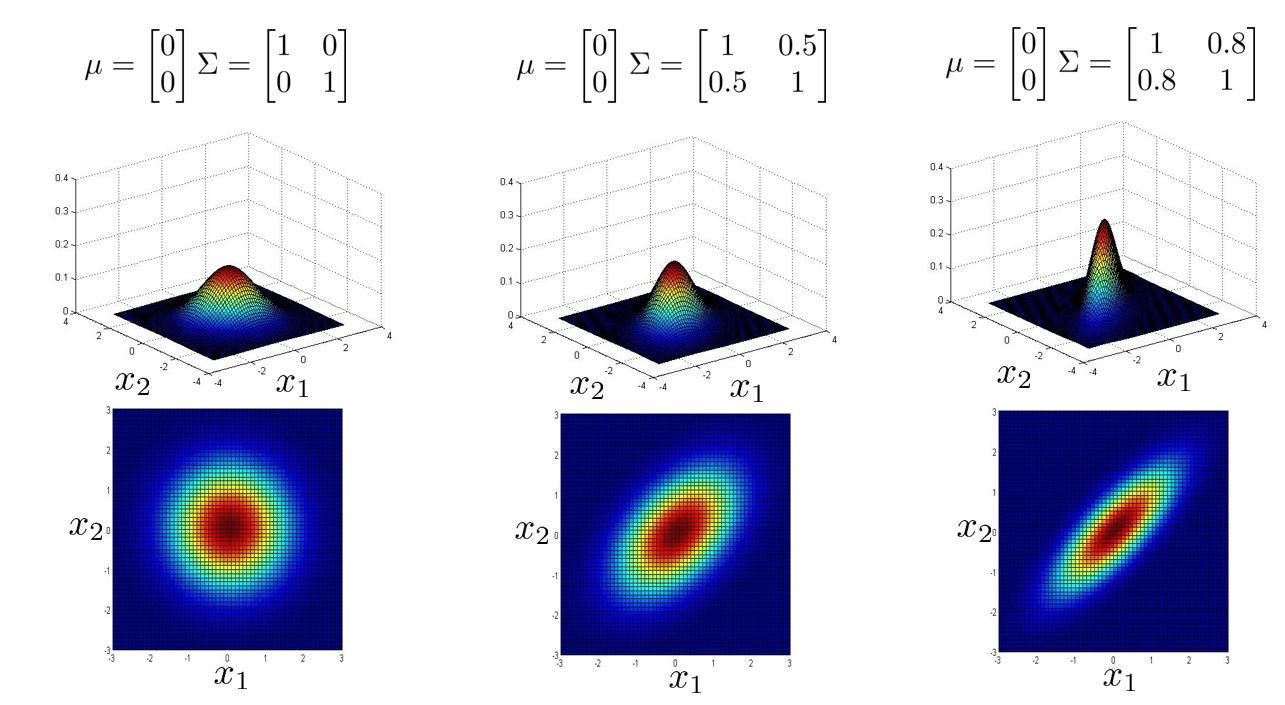
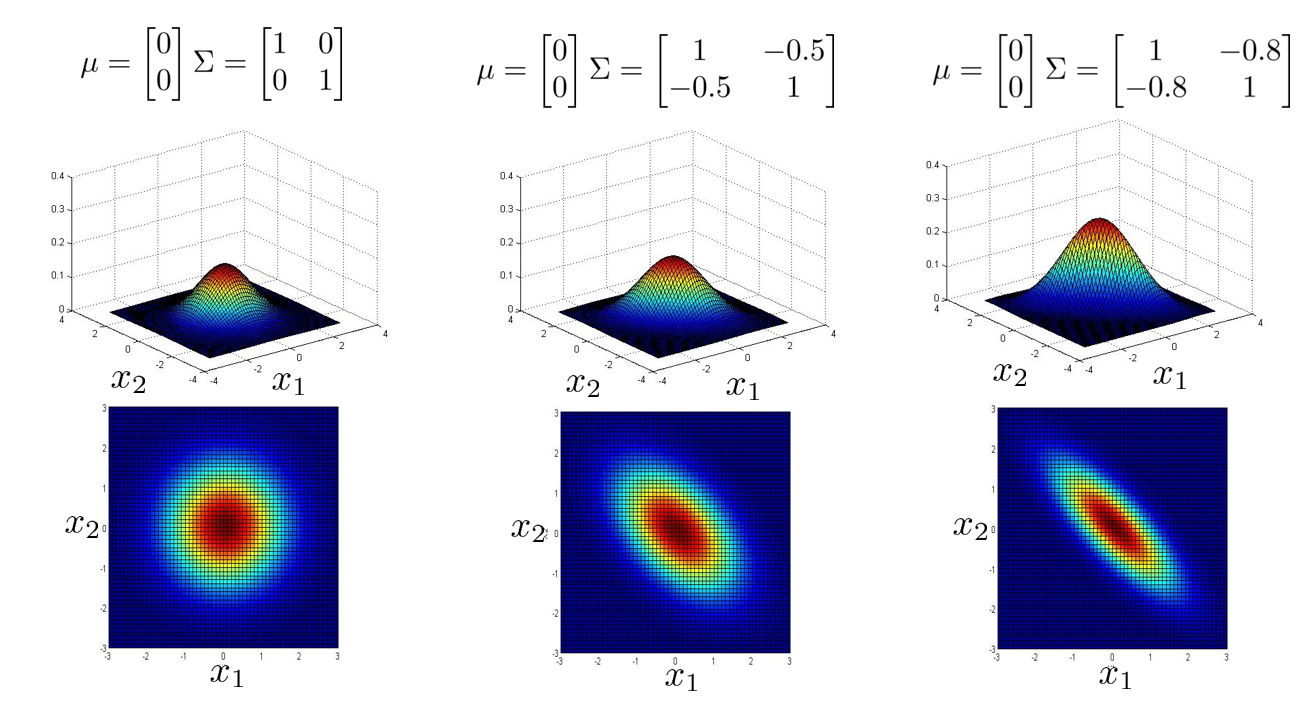
下面两张图中,协方差矩阵 \(\Sigma\) 中除正对角线之外,其他地方也有非 0 值,这时多元高斯分布会捕获一些正相关或负相关的概率图形,可以看到它们已经不是轴对称了,而是对角线对称。
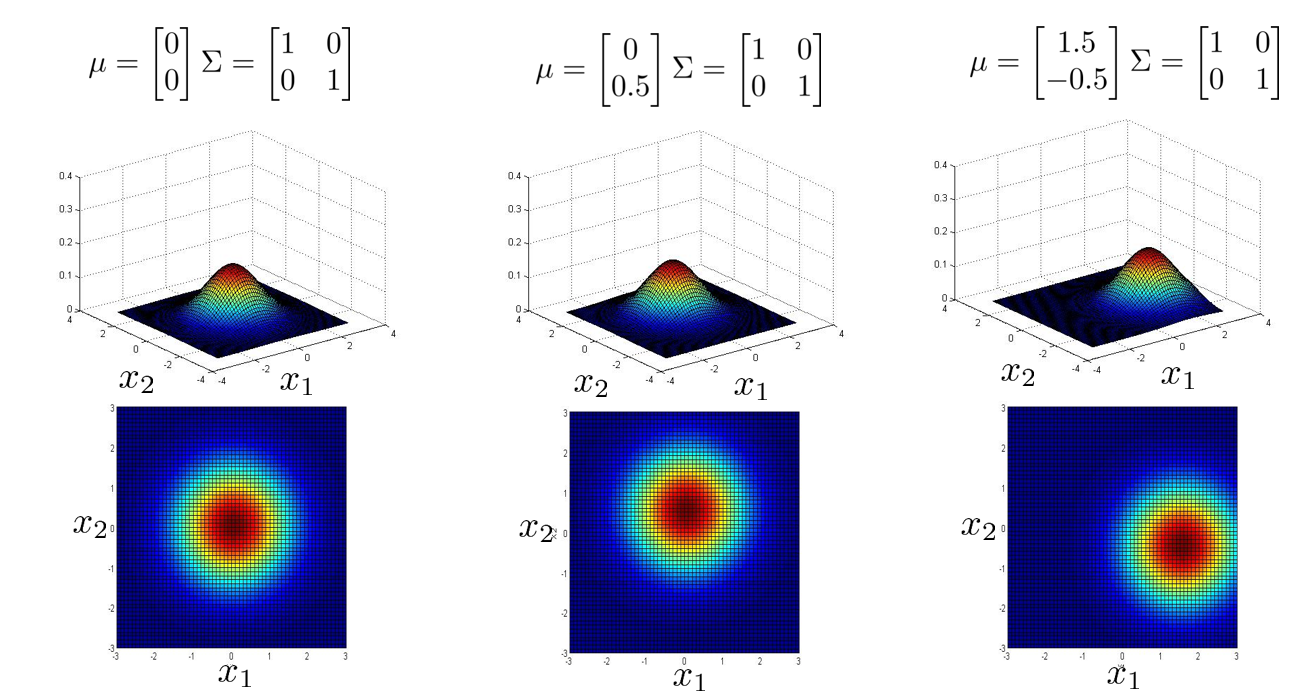
下面最后一张图,实验的是改变 \(\mu\) 的值,可以看到中心点发生了改变。
Anomaly Detection using the Multivariate Gaussian Distribution - Optional
具体步骤:

通过上面的步骤应用多元高斯分布来构建异常检测模型之后,就可以成功捕获到上图中的那个异常点了。
原始模型和多元高斯模型对比与选择:

- 多元高斯分布会自动捕获特征之间的相关性,而原始模型的高斯分布不会,必须要手动选择或添加特征,例如检测数据中心计算机的例子中新添加的特征 \(\frac{\text{CPU load}}{\text{network triffic}}\)
- 多元高斯分布由于需要计算逆矩阵,计算成本高。原始模型的高斯分布计算量小。
- 多元高斯分布由于需要计算逆矩阵,需保证 \(m > n\),具体是 \(m \geq 10n\),否则会出现不可逆现象。此外,如果有冗余(线性相关)的特征也会导致不可逆。此情况,几率低,如出现删除冗余特征即可。
程序代码
直接查看Anomaly detection.ipynb可点击
获取源码以其他文件,可点击右上角 Fork me on GitHub 自行 Clone。


