[C4] 前馈神经网络(Feedforward Neural Network)

前馈神经网络（Feedforward Neural Network - BP）

常见的前馈神经网络

感知器网络
感知器（又叫感知机）是最简单的前馈网络，它主要用于模式分类，也可用在基于模式分类的学习控制和多模态控制中。感知器网络可分为单层感知器网络和多层感知器网络。

BP网络
BP网络是指连接权调整采用了反向传播（Back Propagation）学习算法的前馈网络。与感知器不同之处在于，BP网络的神经元变换函数采用了S形函数（Sigmoid函数），因此输出量是0~1之间的连续量，可实现从输入到输出的任意的非线性映射。

RBF网络
RBF网络是指隐含层神经元由RBF神经元组成的前馈网络。RBF神经元是指神经元的变换函数为RBF（Radial Basis Function，径向基函数）的神经元。典型的RBF网络由三层组成：一个输入层，一个或多个由RBF神经元组成的RBF层（隐含层），一个由线性神经元组成的输出层。

定义符号（Symbol Definition）

• \(a_{i}^{(j)}\) = 第 \(j\) 层 第 \(i\) 个 Unit
• \(s_j\) = 第 \(j\) 层单元数（不包括 Bias Unit）
• \(s_{j+1}\) = 第 \(j+1\) 层单元数（不包括 Bias Unit）
• \(\Theta^{(j)}\) = \(j\) 层到 \(j+1\) 层的 Parameters Matrix
• \(\Theta^{(j)}\) 的 Deimension = \(s_{j+1}\) x \((s_j + 1)\)
• \(a^{(j)}\) 的 Deimension = \((s_j + 1)\) x 1, +1 'cause added one Bias Unit
• \(\Theta^{(j)}\) x \(a^{(j)}\) 的 Deimension = \(\big[s_{j+1}\) x \((s_j + 1)\big]\) x \(\big[(s_j + 1)\) x \(1\big]\) = \(\big[s_{j+1}\) x \(1\big]\)
• \((s_j + 1)\) 中的 '+1' 是因为 \(\Theta^{(j)}\) 和 \(a^{(j)}\) 均添加了 Bias Unit 1
• \(L\) = 神经网络的层数
• \(s_l\) = 第 \(l\) 层的单元数（不包括 Bias Unit）
• \(K\) = 输出单元数 = \(s_L\)
• Input Layer = 第一层 = \(A^{(1)}\)
• Hidden Layer = 第二层 到 \(L-1\) 层 = \(A^{(2)}\) ~ \(A^{(L-1)}\)
• Output Layer = 第 \(L\) 层 = \(A^{(L)}\)
• \(\delta_j^{(l)}\) = 单训练样本时，第 \(l\) 层 第 \(j\) 个节点的误差
• \(\delta^{(l)}\) = 单训练样本时，第 \(l\) 层 所有节点的误差（error）向量
• \(\Delta^{(l)}\) = 所有训练样本时，第 \(l\) 层 所有节点的误差（error）矩阵
• \(D^{(l)}\) = 网络中 第 \(l\) 层的 梯度 矩阵（反向传播算法就是为了计算它）

注 ：在一般情况下，用大写字母表示矩阵，用小写字母表示向量。

逻辑回归和神经网络的代价函数对照（Cost Function）

\[\begin{align} J(\Theta)= & - \frac{1}{m} \cdot \sum\limits_{i=1}^m \Bigg[ y^{(i)} log \big( h_\theta(x^{(i)}) \big) +(1-y^{(i)}) log \big(1 - h_\theta(x^{(i)}) \big) \Bigg] \\ & + \frac{\lambda}{2m} \sum\limits_{j=1}^{n} \theta_j^2 \quad \text{逻辑回归代价函数} \\ J(\Theta)= & - \frac{1}{m} \cdot \sum\limits_{i=1}^m \sum\limits_{k=1}^K \Bigg[ y_k^{(i)} log \Big( \big( h_\Theta(x^{(i)}) \big)_k \Big) +(1-y_k^{(i)}) log \Big(1 - \big( h_\Theta(x^{(i)}) \big)_k \Big) \Bigg] \\ & + \frac{\lambda}{2m} \sum\limits_{l=1}^{L-1} \sum\limits_{i=1}^{S_l} \sum\limits_{j=1}^{S_{l+1}} \big( \Theta_{j i}^{(l)} \big)^2 \quad \text{神经网络代价函数} \end{align} \]

神经网络成本函数是逻辑回归中使用的成本函数的推广
双和 只是将输出层中每个单元计算的逻辑回归成本相加
三重平方和 是将整个网络中的Θ相加（每一层 / 每一列 / 每一行 的元素相加），i 与训练示例中的 i 无关

反向传播算法概览（Backpropagation）

“反向传播“ 是最小化神经网络代价函数的一个术语，可以帮我们计算参数 \(\Theta\) 每次更新的梯度。

与 线性回归 和 逻辑回归 使用梯度下降算法一样，目标：\(\min\limits_{\Theta} J(\Theta)\)

所以，需要写代码来计算 代价函数值 和 更新的梯度值，即： \(J(\Theta)\) 和 \(\frac{\partial}{\partial\Theta_{i j}^{(l)}}J(\Theta)， \quad \Theta_{i j}^{(l)} \in \mathbb R\)

线性回归 和 逻辑回归 的梯度可以用 向量 表示，而神经网络因为涉及 多层结构，每层 多个单元（每个单元就是一个逻辑回归），每个单元又对应 多个 \(\Theta\)，所以神经网络的梯度需要用 多个矩阵 来表示。

用 \(D^{(l)}\) 来表示网络中第 \(l\) 层的 梯度 矩阵，反向传播算法就是为了计算出所有层的 梯度 矩阵，然后传递给优化后的高级梯度下降计算函数（Octave 中的 fmincg 或 fminunc），经过多次迭代之后，获取最优的参数解 \(\Theta\)，然后再用最优解通过正向传播方法来进行预测。

Forward propagation & Back propagation algorithm（Gradient computation）

以编程题中的例子为例（识别手写数字 0 - 9），三层的神经网络，输入层 X，即 \(A^{(1)}\) 有400个特征（20 x 20 像素的图片），共有5000个训练样本，隐藏层 \(A^{(2)}\) 有 25 个单元，输出层 \(A^{(3)}\) 有10个单元（分类）即：（0 - 9），如下图所示：

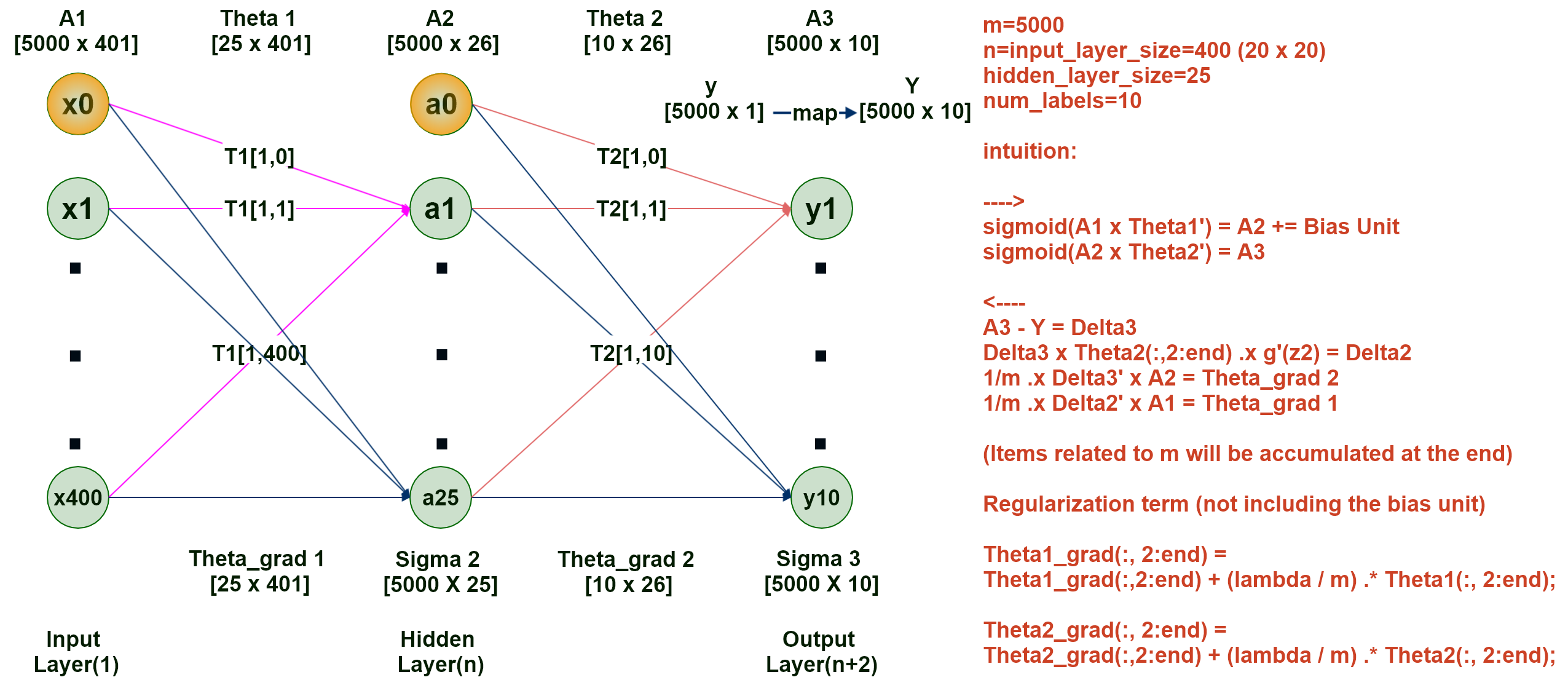
注：在理解时可先把m换成1，清楚之后，再把m换成5000，即先搞懂单个样本（向量）的计算方法，再研究所有样本(5000个)（矩阵）一起计算的方法。
另：输出层（0~9）需要表示成由 0 和 1 组成的 向量（当表示全部样本时为 m x 10 的 矩阵 ）的形式，例如：

• 1 = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
• 5 = [0, 0, 0, 0, 1, 0, 0, 0, 0, 0]
• 9 = [0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
• 0 = [0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
• etc.

而在 预测 时，会将 y 中概率最大的项的索引（从1开始）返回，作为预测结果，例如；

• [0.1, 0.1, 0.9, 0.1, 0.1, 0.2, 0.3, 0.5, 0.2, 0.1]，预测结果为 3
• [0.1, 0.1, 0.3, 0.1, 0.1, 0.2, 0.3, 0.5, 0.2, 0.9]，预测结果为 0
• [0.9, 0.1, 0.2, 0.1, 0.1, 0.2, 0.3, 0.5, 0.2, 0.1]，预测结果为 1
• etc.

正向传播 在直觉上也可试着用多层，每层多个 逻辑回归 （激活函数 activation function）来理解：

1. 先计算第二层的 \(A^{(2)}\)，即：\(A^{(2)} = g(A^{(1)}\) x \({\Theta^{(1)}}^T)\)
2. 将 \(A^{(2)}\) 添加偏置单元（Bias Unit）
3. 再计算第三层（输出层）的 Y（\(A^{(3)}\)），即：\(A^{(3)} = g(A^{(2)}\) x \({\Theta^{(2)}}^T)\)

如此，我们就完成了一次正向的传播，也得到了一个预测的 Y 值。

接着，我们可以从这个预测出的 Y 值出发，进行反向计算（反向传播算法），来得出这一次需要更新的 梯度。

反向传播 需要三个步骤：

1. 首先需要计算出 每一层的每个单元的误差（小写的 \(\delta\) 表示单训练样本时单层所有单元的误差向量，大写的 \(\Delta\) 表示所有训练样本时，单层所有单元的误差矩阵）

   \(\Delta^{(3)} = A^{(3)} - Y\)

   \(\Delta^{(2)} = \Delta^{(3)}\) x \(\Theta^{(2)}(不含偏置单元)\) .x \(g'(Z^{(2)})\)，注 \(Z^{(2)} = A^{(1)}\) x \({\Theta^{(1)}}^T\)

   注 ：\(g^{'}(Z^{(l)}) = \frac{d}{dz}g(Z^{(l)}) = g(Z^{(l)})(1-g(Z^{(l)})) = A^{(l)}\) .x \((1 - A^{(l)})\)
       and where \(sigmoid(z)=g(z)=\frac{1}{1+e^{-z}}\).

2. 然后用误差（error，即：\(\Delta\)）计算出 未正则化 的 梯度 值 \(D^{(l)}\)

   \(D^{(2)} = \frac{1}{m}\) .x \(({\Delta^{(3)}}^T\) x \(A^{(2)})\)

   \(D^{(1)} = \frac{1}{m}\) .x \(({\Delta^{(2)}}^T\) x \(A^{(1)})\)

3. 最后得到 正则化后 的 梯度 值 \(D^{(l)}\)，并返回：

   将 \(D^{(2)}\) 中 除偏置单元以外 的 所有项 均 .+ \((\frac{\lambda}{m})\) .x \(\Theta^{(2)}\)（\(\Theta\) 不含偏置单元）

   将 \(D^{(1)}\) 中 除偏置单元以外 的 所有项 均 .+ \((\frac{\lambda}{m})\) .x \(\Theta^{(1)}\)（\(\Theta\) 不含偏置单元）

   将最终的 梯度 矩阵（\(D^{(1)}\) 和 \(D^{(2)}\)）返回。

展开参数（Unrolling parameters）

在编写完用来计算 \(J(\Theta)\) 和 \(\frac{\partial}{\partial\Theta_{i j}^{(l)}}J(\Theta)\) 的函数代码后，当它被调用时，需要传入 \(\Theta\) ，并且返回 \(D\)，而此处它们都是多个矩阵的形式：

\(\Theta^{(1)}, \Theta^{(2)}\) - Matrices ( Theta1, Theta2)
\(D^{(1)}, D^{(2)}\) - Matrices ( D1, D2)

所以我们需要在将多个 \(\Theta\) 矩阵先转换为多个向量，再将多个向量拼接成一个向量，然后传入函数计算。
而在函数里面，接收到参数后，会将其转换回原来的多个矩阵，从而进行之后的计算逻辑。
同样，当函数需要返回多个矩阵 D 时，也会做如此转换，即返回一个向量。
而当我们在函数外面接收到它返回的向量 D 时，再将其转换回原来的多个矩阵，从而再进行之后的计算逻辑。

梯度检测（Gradient checking - Numerical estimation of gradients）

在编写完用来计算 \(J(\Theta)\) 和 \(\frac{\partial}{\partial\Theta_{i j}^{(l)}}J(\Theta)\) 的函数代码后，为了确保该段代码计算梯度的正确性，可以使用 有限差分法 计算出梯度的近似值，然后用该值与你的代码计算出的梯度进行比对来检查梯度计算的正确与否。有限差分法（finite differences），是微分方程解的近似值。

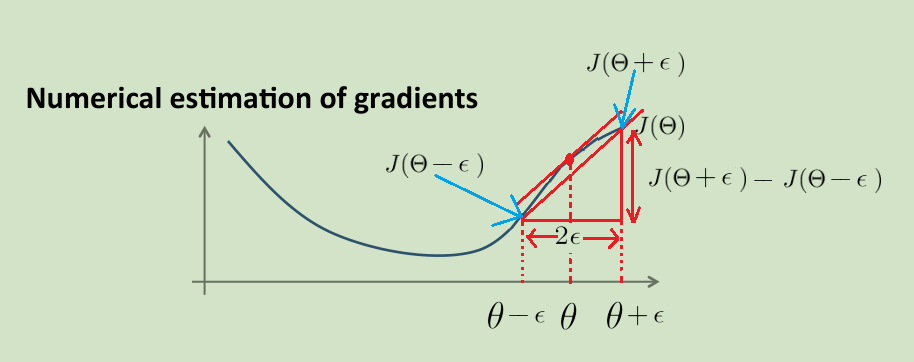
可以看到上图中，两条直线的斜率是及其近似的。

所以 ：\(\frac{\partial}{\partial \theta} J(\theta) \approx \frac{J(\theta + \epsilon) - J(\theta - \epsilon)}{2 \epsilon}\)，\(\epsilon = 10^{-4}\)

上面使用的是偏导数（Partial Derivative）符号\(\partial\)，所以，需要对每一个 \(\theta\) 单独计算数值梯度。在代码中可使用 loop 遍历的方式来实现。

整体的梯度检测流程为：

• 创建一个小的神经网络
• 初始化输入层，隐藏层，输出层数量，以及每层单元数
• 初始化 Theta，X，Y
• 使用你编写的梯度计算代码计算梯度
• 使用你编写的代价计算代码来计算数值估计的梯度
• 比较两个梯度，确保它们及其的近似 - the relative difference will be small (less than 1e-9)

可以看到，本质上其实是使用你编写的 代价 （\(\frac{J(\theta + \epsilon) - J(\theta - \epsilon)}{2 \epsilon}\)）计算代码来 debug 你编写的 梯度 计算代码

注 ：当进行完梯度检测之后，需将这部分代码注释掉，切记千万不要在你训练神经网络模型时，每次迭代都调用一次梯度检测，如此，你的训练会变得非常的慢。

随机初始化 \(\Theta\)（Random initialization）

如果将 \(\Theta\) 的所有项都初始化为 0，那么在每次更新之后，对应于进入所有隐藏单元的输入参数将会是相同的，所以最好的办法是随机初始化，打破对称性（symmetry breaking）。

初始化每一个 \(\Theta_{ij}^{(l)}\) 为一个在 [ - \(\epsilon\), \(\epsilon\) ] 之间的随机值

E.g.

INIT_EPSILON = 0.12;
Theta1 = rand(25, 401) * (2 * INIT_EPSILON) - INIT_EPSILON; 

Putting them together

Pick a network architecture (connectivity pattern between neurons)

• No. of input units : Dimension of features \(x^{(i)}\)
• No. of output units : Number of classes
• No. of hidden layer : Reasonable default : 1, or if > 1 hidden layer, have same no. of hidden units in every layer (usually the more the better)

Training a neural network

1. Randomly initialize weights
2. Implement forward propagation to get \(h_\Theta(x^{(i)})\) for any \(x^{(i)}\)
3. Implement code to compute cost function \(J(\Theta)\)
4. Implement backpropagation to compute partial derivatives \(\frac{\partial}{\partial \theta_{ik}^{(l)}} J(\theta)\)
   for i = 1:m
   Perform forward propagation and backpropagation using example (\(x^{(i)},y^{(i)}\))
   (Get activations \(a^{(l)}\) and delta term \(\delta^{(l)}\) for \(l\) = 2, ..., L).
5. Use gradient checking to compare \(\frac{\partial}{\partial \theta_{ik}^{(l)}} J(\theta)\) computed using backpropagation vs. using numerical estimate of gradient of \(J(\Theta)\)
   Then disable gradient checking code.
6. Use gradient descent or advanced optimization method with backpropagation to try to minimize \(J(\Theta)\) as a function of parameters \(\Theta\)

程序代码

直接查看BP Neural Network.ipynb可点击

获取源码以其他文件，可点击右上角 Fork me on GitHub 自行 Clone。