[C1] 线性回归(Linear Regression)
线性回归(Linear Regression with One / Multiple Variable)
定义符号(Symbol Definition)
- m = 数据集中训练样本的数量
- n = 特征的数量
- x = 输入变量 / 特征
- y = 输出变量 / 目标变量
- (x, y) 表示一个训练样本
- \(x^{(i)}\) 训练集中第 i 个样本
- \(x_j^{(i)}\) 训练集中第 i 个样本中第 j 个特征
假设函数(Hypothesis Function)
以下所有 \(x_0^{(i)} \equiv 1\)
\(h_\theta (x^{(i)}) = \theta_0x_0^{(i)} + \theta_1x_1^{(i)} + \theta_2x_2^{(i)} + ... + \theta_nx_n^{(i)}\)
\(\theta=\begin{bmatrix}\theta_0\\\theta_1\\\theta_2\\.\\.\\.\\\theta_n\end{bmatrix}\quad\in\mathbb{R^{n+1}},\qquad x^{(i)}=\begin{bmatrix}x_0^{(i)}\\x_1^{(i)}\\x_2^{(i)}\\.\\.\\.\\x_n^{(i)}\end{bmatrix}\quad\in\mathbb{R^{n+1}},\qquad X=\begin{bmatrix}x_0^{(1)},x_1^{(1)},x_2^{(1)},...x_n^{(1)}\\x_0^{(2)},x_1^{(2)},x_2^{(2)},...x_n^{(2)}\\x_0^{(3)},x_1^{(3)},x_2^{(3)},...x_n^{(3)}\\\quad.\\\quad.\\\quad.\\x_0^{(m)},x_1^{(m)},x_2^{(m)},...x_n^{(m)}\\\end{bmatrix}\)
\(h_\theta (x^{(i)}) = \theta^T x^{(i)} = X \theta\)
代价函数(Cost Function)
\(J(\theta_0, \theta_1,···\theta_n) = \frac 1{2m}\sum\limits_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2\)
梯度下降(Gradient Descent)
重复,直到收敛(Repeat until convergence):
\(\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1,···\theta_n)\), 其中 \(\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1,···\theta_n)\) 计算方法为对 \(\theta_j\) 求偏导数(partial derivative)
即(We can work out the derivative part using calculus to get):
\(\theta_j := \theta_j - \alpha\frac{1}{m}\sum\limits_{i = 1}^{m}\biggl(h_\theta(x^{(i)}) - y^{(i)}\biggl)\cdot x_j^{(i)}\)
同时更新(simultaneously update)\(\theta_j\), for j = 0, 1 ..., n
另外, \(x_0^{(i)} \equiv 1\)
特征缩放 - 加速梯度下降的收敛(Feature Scaling)
一个机器学习问题,且有多个特征,如果不同特征取值都处在一个相近范围,那么梯度下降法可更快收敛。正规方程法时,无需归一化特征变量。
通常目的是将特征的取值约束在 -1 到 +1 的范围内。 而 \(x_0 \equiv 1\) 已在这个范围内,所以无需做归一化处理。
-1 和 +1 这两个数字并不是太重要:
\(0\leq x_1\leq 3\quad √\)
\(-2\leq x_2\leq 0.5\quad √\)
\(-100\leq x_3\leq 100\quad ×\)
\(-0.0001\leq x_4\leq 0.0001\quad ×\)
下面这些典型的范围也都可以接受:
\(-3\leq x_1\leq 3\quad √\)
\(-\frac 13\leq x_2\leq \frac 13\quad √\)
均值归一化(mean normalization)
$ x_n = \frac{x_n - \eta_n}{S_n}, \quad \eta_n $ 为平均值, \(S_n\) 为 最大值 - 最小值, 也可以用标准差(Standard Deviation)来代替。
标准差 = 方差的算术平方根 = \(\sqrt{ \frac{1}{N} \cdot \sum\limits_{i = 1}^{N} (x_i - \eta_n)^2 }\)
特征缩放其实无需太精确,其目的只是为了让梯度下降能够运行得更快一点,让梯度下降收敛所需的循环次数更少一些而已。
调试梯度下降,选择适合的 \(\alpha\)(Debugging Gradient Descent)
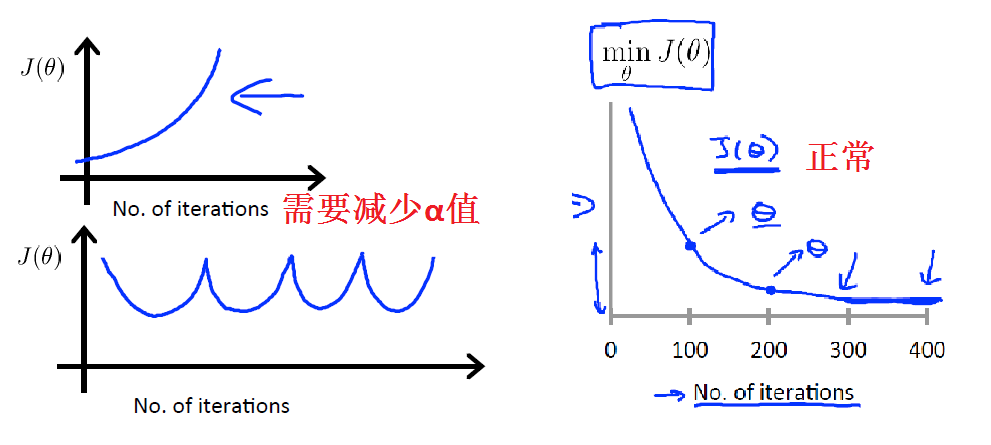
调试梯度下降,在坐标系中的x轴上画一个迭代次数,y轴 J(θ) 的图,如果随着下降法的迭代次数增加 J(θ) 的值呈现出增加或波浪形式,那么你可能需要降低 \(\alpha\)。
已经证明如果学习速率α足够小,那么J(θ)将在每个迭代中减少。
\(\alpha\) 太小,收敛慢;\(\alpha\) 太大,不收敛还有可能会发散。
选择 \(\alpha\) 的经验是:...,0.001,0.003,0.01,0.03,0.1,0.3,1,... ,找到 \(\alpha\) 的最大值,然后选择比最大值略小的 \(\alpha\) 值。
特征的选择方法与多项式回归(Features and Polynomial Regression)
当线性假设函数不能很好拟合现有样本时,可以通过对特征值进行平方、立方或开方来进行调整,即使用多元线性回归算法来拟合数据。
值得注意的是这种选择特征的方式,那么归一化就显得非常重要了,因为特征之间的差距非常大。
以后可以使用一个算法,观察给出的数据,并自动为你选择到底应该选择一个二次函数或者一个三次函数,还是别的函数。
通过采取适当的角度来观察特征就可以得到一个更符合你的数据的模型。
正规方程法(最小二乘法)求解多元线性回归 (Normal Equation)

对于上面的数据集,使用\(\theta = (X^TX)^{-1}X^Ty\) 可以直接求出最优解的 \(\theta\) 向量。
正规方程与梯度下降对比(Normal Equation VS Gradient Descent)
这里列举了一些它们的优点和缺点(假如你有 m 个训练样本和 n 个特征变量):
使用正规方程,不需要归一化特征变量,但是如果使用梯度下降,就需要对特征变量进行归一化。
梯度下降法的缺点之一就是,你需要选择学习速率 \(\alpha\),这通常表示需要运行多次,尝试不同的学习速率 \(\alpha\),然后找到运行效果最好的那个,所以这是一种额外的工作和麻烦。
梯度下降法的另一个缺点是,它需要更多次的迭代,因为一些细节,计算可能会更慢。
至于正规方程,你不需要选择学习速率 \(\alpha\) 所以就非常方便,也容易实现,你只要运行一下,通常这就够了,并且你也不需要迭代,所以不需要画出 J(θ) 的曲线来检查收敛性或者采取所有其他额外的步骤。
梯度下降法在有很多特征变量的情况下也能运行地相当好,所以即使你有上百万的特征变量,你可以运行梯度下降法,并且通常很有效,它会正常的运行。
相对于正规方程法,为了求解参数 θ 需要求解这一项 X 转置乘以 X 的逆,它是一个 \(n*n\) 的矩阵,而实现逆矩阵计算所需要的计算量,大致是矩阵维度的三次方,因此计算这个逆矩阵需要计算大致 \(O(n^3)\),有时稍微比计算 \(O(n^3)\) 快一些,但是对我们来说很接近,所以如果特征变量的数量 n 很大的话,那么计算这个量会很慢。
千位数乘千位数的矩阵做逆变换,对于现代计算机来说实际上是非常快的,但如果 n 上万,那么我可能会开始犹豫,上万乘上万维的矩阵作逆变换,会开始有点慢。
总结一下,只要特征变量数量小于一万,我通常使用正规方程法,而不使用梯度下降法。
随着我们要讲的学习算法越来越复杂,例如,当我们讲到分类算法,像逻辑回归算法,我们会看到,实际上对于那些算法,并不能使用正规方程法,我们将不得不仍然使用梯度下降法。因此,梯度下降法是一个非常有用的算法,可以用在有大量特征变量的线性回归问题,或者我们以后在课程中,会讲到的一些其他的算法。因为,标准方程法不适合或者不能用在它们上,但对于这个特定的线性回归模型,正规方程法是一个比梯度下降法更快的替代算法。所以,根据具体的问题,以及你的特征变量的数量,这两算法都是值得学习的。
正规方程不可逆问题(Normal Equation Non-invertibility)
有些矩阵可逆的,而有些矩阵不可逆的,我们称那些不可逆矩阵为奇异矩阵或退化矩阵,问题的重点在于 \(X^TX\) 的不可逆问题很少发生。在用 Octave 实现正规方程时,我们可以使用 pinv 函数代替 inv 函数。pinv 函数将给出 θ 的值,即使 \(X^TX\) 是不可逆的。
如果 \(X^TX\) 是不可逆的,则常见的原因可能是:
-
有冗余特征:其中两个特性非常密切相关(即,它们是线性相关的),可以删除线性相关的其中一个特征来解决不可逆的问题。例如,在预测住房价格时,如果 x1 是以英尺为单位,\(x_2\) 是以平方米为单位。同时 你也知道 1 米等于 3.28 英尺 ( 四舍五入到两位小数 ) 。因此,你的这两个特征值将总是满足约束 \(x_1\) 等于 3.28 平方米乘以 \(x_2\)。而此时,矩阵 \(X^TX\) 将是不可逆的。
-
特征过多 (e.g. m ≤ n) :删除多余的特征或者使用正则化来解决不可逆的问题。
程序代码
直接查看Linear regression.ipynb可点击
获取源码以其他文件,可点击右上角 Fork me on GitHub 自行 Clone。



