GCM模式查表优化

一、GCM介绍

GCM 是分组密码的一种工作模式，具体细节可通过 NIST 的文档了解

Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC

二、GHash查表优化

查表优化的思想就是利用预处理生成查找表，在正式运算时利用查表节约操作开销，该优化方案在 OpenSSL 和 Oryx Embedded 这两个密码库中都有采用。

优化算法论文为 D. McGrew and J. Viega 的 The Galois/Counter Mode of Operation (GCM)

2.1 GHash模块

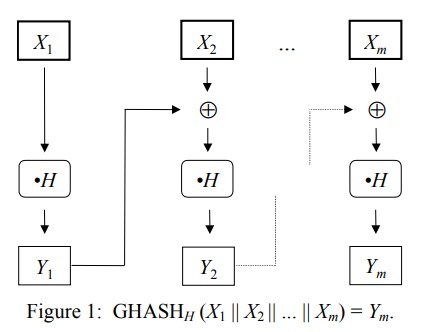
GHash 模块的结构与 CFB 模式类似，记每一轮输入为 \(X_i\)，输出为 \(Y_i\)。那么

\[Y_i = (Y_{i-1} \oplus X_i) \cdot H \]

其中 \(Y_1 = X_1 \cdot H\)，乘法为 \(GF(2^{128})\) 有限域乘法，\(X_i\) 长度为 128bit

合并后表达式如下

\[Y_m = \text{GHash}_H(X_1|X_2|\cdots|X_m) = ((((X_1 \cdot H) \oplus X_2) \cdot H ) \oplus \cdots \oplus X_m) \cdot H \]

2.2 \(GF(2^{128})\) 有限域乘法 gmul 模块

\(GF(2^{128})\) 中使用的不可约多项式为 \(p(x)=1+x+x^2+x^7+x^{128}\)

对于一个比特串 \(b_0 b_1 \cdots b_{127}\)，其对应的多项式为 \(b_0 + b_1 x + b_{127} x^{127}\)。例如，不可约多项式 \(p(x)\) 对应的比特串为 \(E1|(0 \cdots 0)_{120}, \; E1=11100001\)

2.3 有限域乘法查表优化

将表达式 \(X \cdot H\) 进一步展开成 \(X = b_0 + b_1 x^8 + \cdots + b_{15} x^{120}\)，有

\[\begin{array}{ll} X \cdot H &= (b_0 H) + (b_1 H) \cdot x^8 + \cdots + (b_{15} H) \cdot x^{120}\\ &=( ( b_{15} H \cdot x^8 + b_{14} H) \cdot x^8 \cdots ) \cdot x^8 + b_0 H \end{array} \]

其中 \(b_i\) 是 8 比特数，故可预先生成查找表 \(\text{HTable}(a) = a \cdot H, \; a \in [0, 255]\)，将 \(b_i \cdot H\) 转化为查表操作

查找表可以通过如下公式递推生成，记 \(a = a_0 + a_1 x + \cdots a_7 x^7\)

• \(\text{HTable(0)} = 0, \text{HTable(1)} = H\)
• 若 \(a_0 = 0\)，那么 \(\text{HTable(a)} = x \cdot \text{HTable(a / x)}\)
• 若 \(a_0 = 1\)，那么 \(\text{HTable(a)} = H \oplus \text{HTable(a - 1)}\)

此外，对于 \(x^8\) 乘法等价于直接移位，将会溢出 8 比特数据位，这部分也通过预先生成的查找表 \(\text{ReduceTable}(a) = a \cdot x^{128} \equiv a \cdot (1+x+x^2+x^7) \bmod p\)，利用查表完成模操作

注：除了像上述以 8 比特为单位外，还可以 4 比特为单位。虽然速率有所降低，但所需要的查找表大小大幅减小。

三、代码实现

GCM的代码我已经开源至我自己写的密码库GMLib中，下面截取其中的有限域乘法gmul模块

3.1 功能函数

首先是大端读入与存储的功能函数

/// @brief 大端读入64比特整数
static uint64_t loadu64(uint8_t* in) {
    uint64_t r = 0;
    for (int i = 0; i < 8; i++) {
        r = (r << 8) | in[i];
    }
    return r;
}

/// @brief 大端存入64比特整数
static void storeu64(uint8_t* out, uint64_t n) {
    for (int i = 7; i >= 0; i--) {
        out[i] = n & 0xFF;
        n >>= 8;
    }
}

3.2 gmul 普通实现

NIST 文档 p13-14 页已经给出 gmul 的伪代码，通过该伪代码可以得到 gmul 的普通实现

void gmul_common(uint8_t* res, uint8_t* X, uint8_t* Y) {
    // Rh = E100...00 (64bit)
    uint64_t Rh = (uint64_t)0xE1 << 56;
    // 定义128bit数Z，区分高64位和低64位
    uint64_t Zh = 0, Zl = 0;
    // 定义128bit数V，区分高64位和低64位，并从Y对应的内存中加载
    uint64_t Vh = loadu64(Y), Vl = loadu64(Y + 8);
    // 进行乘法
    for (int i = 0; i < 16; i++) {
        uint8_t x = X[i];
        for (int j = 7; j >= 0; j--) {
            if ((x >> j) & 1) {
                Zh ^= Vh, Zl ^= Vl;
            }
            int t = Vl & 1;
            Vl = (Vh << 63) | (Vl >> 1);
            Vh = Vh >> 1;
            if (t) {
                Vh ^= Rh;
            }
        }
    }
    // 将Z存入res中
    storeu64(res, Zh);
    storeu64(res + 8, Zl);
}

3.3 gmul 查表优化实现

查表初始化操作的 \(a\) 递推顺序为 1000 0000, 0100 0000, 1100 0000, ..., 1111 1111。为了解决递推索引顺序与 \(a\) 的差异，定义比特翻转的查找表，即 \(\text{Rev}(b_0 b_1 \cdots b_7) = b_7 \cdots b_0\)。当索引 \(i\) 从 1 递增到 255 时，对应的 \(a = \text{Rev}(i)\) 则从 1000 0000 递增到 1111 1111

static int Rev[256] = {
    0,  128, 64, 192, 32, 160, 96,  224, 16, 144, 80, 208, 48, 176, 112, 240,
    8,  136, 72, 200, 40, 168, 104, 232, 24, 152, 88, 216, 56, 184, 120, 248,
    4,  132, 68, 196, 36, 164, 100, 228, 20, 148, 84, 212, 52, 180, 116, 244,
    12, 140, 76, 204, 44, 172, 108, 236, 28, 156, 92, 220, 60, 188, 124, 252,
    2,  130, 66, 194, 34, 162, 98,  226, 18, 146, 82, 210, 50, 178, 114, 242,
    10, 138, 74, 202, 42, 170, 106, 234, 26, 154, 90, 218, 58, 186, 122, 250,
    6,  134, 70, 198, 38, 166, 102, 230, 22, 150, 86, 214, 54, 182, 118, 246,
    14, 142, 78, 206, 46, 174, 110, 238, 30, 158, 94, 222, 62, 190, 126, 254,
    1,  129, 65, 193, 33, 161, 97,  225, 17, 145, 81, 209, 49, 177, 113, 241,
    9,  137, 73, 201, 41, 169, 105, 233, 25, 153, 89, 217, 57, 185, 121, 249,
    5,  133, 69, 197, 37, 165, 101, 229, 21, 149, 85, 213, 53, 181, 117, 245,
    13, 141, 77, 205, 45, 173, 109, 237, 29, 157, 93, 221, 61, 189, 125, 253,
    3,  131, 67, 195, 35, 163, 99,  227, 19, 147, 83, 211, 51, 179, 115, 243,
    11, 139, 75, 203, 43, 171, 107, 235, 27, 155, 91, 219, 59, 187, 123, 251,
    7,  135, 71, 199, 39, 167, 103, 231, 23, 151, 87, 215, 55, 183, 119, 247,
    15, 143, 79, 207, 47, 175, 111, 239, 31, 159, 95, 223, 63, 191, 127, 255,
};

查表表定义和初始化操作，将查找表 HTable 定义为二维数组，第一维是 a 的索引，第二维分别存储 HTable[a] 的高 64 位和低 64 位

typedef uint64_t HTable[256][2];

/// @brief ghash_init 初始化 HTable
void ghash_init(uint8_t* H, HTable t) {
    uint64_t Hh, Hl;
    Hh = loadu64(H);
    Hl = loadu64(H + 8);

    // 初始化HTable[0], HTable[1]
    t[0][0] = 0, t[0][1] = 0;
    t[Rev[1]][0] = Hh, t[Rev[1]][1] = Hl;
    for (int i = 2; i < 256; i++) {
        // 奇数: M(i) = M(i-1) + M(1)
        if (i & 1) {
            t[Rev[i]][0] = t[Rev[i - 1]][0] ^ t[Rev[1]][0];
            t[Rev[i]][1] = t[Rev[i - 1]][1] ^ t[Rev[1]][1];
        }
        // 偶数: M(i) = M(i/2) * x
        else {
            uint64_t* m = t[Rev[i / 2]];
            // R = 1110 0001 | 0(120)
            uint64_t Rh = (uint64_t)0b11100001 << (64 - 8);
            //  >> 1
            t[Rev[i]][1] = (m[0] << 63) | (m[1] >> 1);
            t[Rev[i]][0] = m[0] >> 1;
            // mod
            if (m[1] & 1) {
                t[Rev[i]][0] ^= Rh;
            }
        }
    }
}

定义 ReduceTable

static uint16_t ReduceTable[256] = {
    0x0000, 0x01c2, 0x0384, 0x0246, 0x0708, 0x06ca, 0x048c, 0x054e, 0x0e10,
    0x0fd2, 0x0d94, 0x0c56, 0x0918, 0x08da, 0x0a9c, 0x0b5e, 0x1c20, 0x1de2,
    0x1fa4, 0x1e66, 0x1b28, 0x1aea, 0x18ac, 0x196e, 0x1230, 0x13f2, 0x11b4,
    0x1076, 0x1538, 0x14fa, 0x16bc, 0x177e, 0x3840, 0x3982, 0x3bc4, 0x3a06,
    0x3f48, 0x3e8a, 0x3ccc, 0x3d0e, 0x3650, 0x3792, 0x35d4, 0x3416, 0x3158,
    0x309a, 0x32dc, 0x331e, 0x2460, 0x25a2, 0x27e4, 0x2626, 0x2368, 0x22aa,
    0x20ec, 0x212e, 0x2a70, 0x2bb2, 0x29f4, 0x2836, 0x2d78, 0x2cba, 0x2efc,
    0x2f3e, 0x7080, 0x7142, 0x7304, 0x72c6, 0x7788, 0x764a, 0x740c, 0x75ce,
    0x7e90, 0x7f52, 0x7d14, 0x7cd6, 0x7998, 0x785a, 0x7a1c, 0x7bde, 0x6ca0,
    0x6d62, 0x6f24, 0x6ee6, 0x6ba8, 0x6a6a, 0x682c, 0x69ee, 0x62b0, 0x6372,
    0x6134, 0x60f6, 0x65b8, 0x647a, 0x663c, 0x67fe, 0x48c0, 0x4902, 0x4b44,
    0x4a86, 0x4fc8, 0x4e0a, 0x4c4c, 0x4d8e, 0x46d0, 0x4712, 0x4554, 0x4496,
    0x41d8, 0x401a, 0x425c, 0x439e, 0x54e0, 0x5522, 0x5764, 0x56a6, 0x53e8,
    0x522a, 0x506c, 0x51ae, 0x5af0, 0x5b32, 0x5974, 0x58b6, 0x5df8, 0x5c3a,
    0x5e7c, 0x5fbe, 0xe100, 0xe0c2, 0xe284, 0xe346, 0xe608, 0xe7ca, 0xe58c,
    0xe44e, 0xef10, 0xeed2, 0xec94, 0xed56, 0xe818, 0xe9da, 0xeb9c, 0xea5e,
    0xfd20, 0xfce2, 0xfea4, 0xff66, 0xfa28, 0xfbea, 0xf9ac, 0xf86e, 0xf330,
    0xf2f2, 0xf0b4, 0xf176, 0xf438, 0xf5fa, 0xf7bc, 0xf67e, 0xd940, 0xd882,
    0xdac4, 0xdb06, 0xde48, 0xdf8a, 0xddcc, 0xdc0e, 0xd750, 0xd692, 0xd4d4,
    0xd516, 0xd058, 0xd19a, 0xd3dc, 0xd21e, 0xc560, 0xc4a2, 0xc6e4, 0xc726,
    0xc268, 0xc3aa, 0xc1ec, 0xc02e, 0xcb70, 0xcab2, 0xc8f4, 0xc936, 0xcc78,
    0xcdba, 0xcffc, 0xce3e, 0x9180, 0x9042, 0x9204, 0x93c6, 0x9688, 0x974a,
    0x950c, 0x94ce, 0x9f90, 0x9e52, 0x9c14, 0x9dd6, 0x9898, 0x995a, 0x9b1c,
    0x9ade, 0x8da0, 0x8c62, 0x8e24, 0x8fe6, 0x8aa8, 0x8b6a, 0x892c, 0x88ee,
    0x83b0, 0x8272, 0x8034, 0x81f6, 0x84b8, 0x857a, 0x873c, 0x86fe, 0xa9c0,
    0xa802, 0xaa44, 0xab86, 0xaec8, 0xaf0a, 0xad4c, 0xac8e, 0xa7d0, 0xa612,
    0xa454, 0xa596, 0xa0d8, 0xa11a, 0xa35c, 0xa29e, 0xb5e0, 0xb422, 0xb664,
    0xb7a6, 0xb2e8, 0xb32a, 0xb16c, 0xb0ae, 0xbbf0, 0xba32, 0xb874, 0xb9b6,
    0xbcf8, 0xbd3a, 0xbf7c, 0xbebe,
};

使用上文提及的公式，利用查找表完成 gmul 操作

void gmul_htable(uint8_t* out, uint8_t* in, HTable ht) {
    uint64_t rh = ht[in[15]][0], rl = ht[in[15]][1];
    for (int i = 14; i >= 0; i--) {
        uint8_t rem = rl & 0xFF;
        rl = (rh << 56) | (rl >> 8);
        rh = (rh >> 8) ^ ((uint64_t)ReduceTable[rem] << (64 - 16));

        rh ^= ht[in[i]][0], rl ^= ht[in[i]][1];
    }
    storeu64(out, rh);
    storeu64(out + 8, rl);
}

3.4 调用样例

HTable t;
// H = 01 02 03 04 05 06 07 08 09 0a 0b 0c 00 00 00 00
// x = 01 02 03 04 05 06 07 08 09 0a 0b 0c 00 00 00 00
uint8_t H[16] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12};
uint8_t x[16] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12};
ghash_init(H, t);  // 初始化 HTable
// y = 00 e0 84 e7 10 e6 94 f9 40 22 00 28 00 2a 00 80
uint8_t y[16];
gmul_common(y, x, H);  // 普通乘法
gmul_htable(y, x, t);  // 查表优化

参考资料：D. McGrew and J. Viega. The Galois/Counter Mode of Operation (GCM)