有限域算法

一、有限域介绍

有限域亦称伽罗瓦域（Galois Fields），是伽罗瓦于 18 世纪 30 年代研究代数方程根式求解问题时引出的概念。有限域在密码学、近代编码、计算机理论、组合数学等方面有着广泛的应用

在抽象代数中，域是一个对加法和乘法封闭的集合，其中要求每个元素都有加法逆元，每个非零元素都有乘法逆元。若域 \(F\) 只包含有限个元素，则称为有限域，有限域中元素的个数称为有限域的阶。可以证明，有限域的阶必为素数的幂，即有限域的阶可表示为 pⁿ（p 是素数，n 是正整数）。有限域通常记为 GF(pⁿ)

有限域 GF(pⁿ) 中的元素可以看成有限域 GF(p) 上次数小于 n 的多项式，因此 GF(pⁿ) 构成 GF(p) 上的 n 维线性空间，其中的一组基为 {1, x, x², ......, x^n-1}，所以有限域 GF(pⁿ) 中的所有元素可以用基 {1, x, x², ......, x^n-1} 的线性组合来表示，其线性组合的系数在 GF(p) 中，即 GF(pⁿ) = {a₀ + a₁ x + a₂ x² + ... + a_n-1 x^n-1 | a_i ∈ GF(p), i = 0, 1, 2, ..., n-1}。

若将 GF(p) 上的加法单位元记作 0，乘法单位元记作 1，元素 a 的加法逆元记作 -a，非零元素 b 的乘法逆元记作 b^-1，则有：a + (-a) = 0 (mod p), b × b^-1 = 1 (mod p)。针对 GF(p) 中的元素 a 和非零元素 b，加法是 (a + b) mod p，减法是 (a + (-b)) mod p，乘法是 a × b mod p，除法是 a × b^-1 mod p，该算法对多项式运算同样成立，因此 GF(pⁿ) 上的四则运算可以由 GF(p) 上多项式的四则运算导出。

特别地，当 p=2 时，GF(2ⁿ) 中的元素 a₀ + a₁ x + a₂ x² + ... + a_n-1 x^n-1 可以转化为二进制数 a_n-1 ... a₂ a₁ a₀。因为计算机中使用的是二进制数，且 1 字节为 8 位，所以在密码学中常常用到有限域 GF(2⁸)

二、有限域的四则运算

1. 有限域 GF(2ⁿ) 加法

1.1 原理介绍

GF(2ⁿ) 上的加法即为 GF(2) 上多项式的加法，具体是将 GF(2) 上多项式的系数分别相加。而对于 GF(2) 上的元素，加法即为异或运算。所以，GF(2ⁿ) 上的加法运算即为按位异或运算

1.2 具体实现(python)

def gf2_add(a: int, b: int, poly) -> int:
    """
    :param a: 被加数
    :param b: 加数
    :param poly: 不可约多项式
    :return: 和
    """
    return a ^ b

1.3 测试样例及结果

# 不可约多项式 poly = 0b100011011

0x89 + 0x4d = 0xc4
0xaf + 0x3b = 0x94
0x35 + 0xc6 = 0xf3

2. 有限域 GF(2ⁿ) 减法

2.1 原理介绍

GF(2ⁿ) 上的减法即为 GF(2) 上多项式的减法。具体是将 GF(2) 上多项式的系数分别相减。而对于 GF(2) 上的元素，减法即为加法。所以，GF(2ⁿ) 上的减法即为 GF(2ⁿ) 上的加法

2.2 具体实现(python)

def gf2_sub(a: int, b: int, poly) -> int:
    """
    :param a: 被减数
    :param b: 减数
    :param poly: 不可约多项式
    :return: 差
    """
    return a ^ b

2.3 测试样例及结果

# 不可约多项式 poly = 0b100011011

0x89 - 0x4d = 0xc4
0xaf - 0x3b = 0x94
0x35 - 0xc6 = 0xf3

3. 有限域 GF(2ⁿ) 乘法

3.1 原理介绍

GF(2ⁿ) 上的乘法即为 GF(2) 上多项式的乘法，具体是将 GF(2) 上的两个多项式相乘，但是两个多项式相乘之后的次数可能大于等于 n，因此在计算两个多项式的乘积之后，还需要模一个 GF(2) 上的 n 次不可约多项式，来保证得到的多项式次数小于 n

在具体实现中，模 n 次不可约多项式的操作可以分解到每一次乘 x 的运算中，即乘 x 的运算通过左移一位后再根据条件按位异或给定的不可约多项式对应的 n 位二进制数的后 n-1 位实现。乘 x 的更高次幂可以通过重复使用该方法实现，这样一来，GF(2ⁿ) 上的乘法结果可由多个中间结果相加得到。有限域 GF(2ⁿ) 上乘法运算的详细步骤如下：

1. 输入 a, b 和不可约多项式 poly，并将 a, b 转化为二进制数，将乘法结果 ans 初始化为 0
2. 判断 b 是否大于 0，若大于 0，则转第（3）步，否则转第（6）步
3. 判断 b 的最低位是否为 1，若是，将 ans 与 a 进行按位异或运算，再将 a 左移一位，否则直接将 a 左移一位
4. 判断 a 的最高位（xⁿ 对应位）是否为 1，若是，则将 a 与 poly 进行按位异或运算
5. 将 b 右移一位，转置第（2）步
6. 输出 ans

3.2 流程图

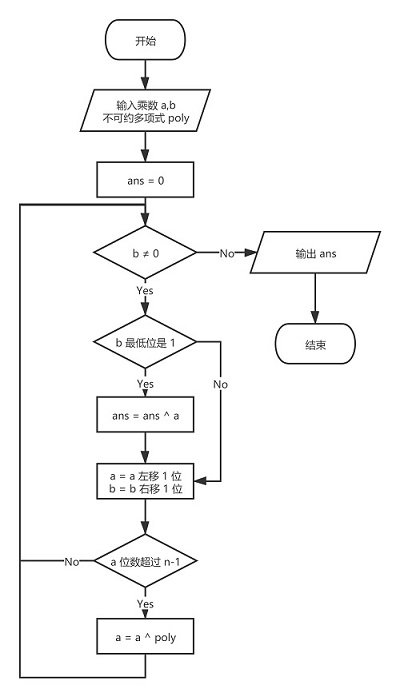
3.3 具体实现(python)

def gf2_mul(a: int, b: int, poly: int) -> int:
    """
    :param a: 被乘数
    :param b: 乘数
    :param poly: 不可约多项式
    :return: 积
    """
    ans = 0
    digit_1 = poly.bit_length() - 1
    while b:
        if b & 1:
            ans = ans ^ a
        a, b = a << 1, b >> 1
        if a >> digit_1:  # 取出 a 的最高位
            a = a ^ poly
    return ans

3.4 测试样例及结果

# 不可约多项式 poly = 0b100011011

0xce * 0xf1 = 0xef
0x70 * 0x99 = 0xa2
0x00 * 0xa4 = 0x00

4. 有限域 GF(2ⁿ) 带余除法

4.1 原理介绍

GF(2ⁿ) 上的除法指 GF(2) 上多项式的带余除法，具体是将 GF(2) 上的两个多项式相除，得到商和余数

在具体实现中，令 a 为被除数，b 为除数，q 为商，r 为余数，且均为二进制数形式。将 q 的值初始化为 0，当 a 的比特长度大于等于 b 的比特长度时，b 左移 k 位后与 a 长度相等，此时将 q 与 1 左移 k 位后的值相加，将 a 与 b 左移 k 位后的值相减，再判断 a 与 b 的大小；若 a 大于等于 b，则重复以上步骤，直至 a 小于 b，此时 a 的值即为 r

有限域上除法运算的详细步骤如下：

1. 输入 a, b，并将 a, b 转化为二进制数，将商 ans 初始化为 0
2. 判断 a 的比特长度是否大于等于 b 的比特长度，若是，则转第（3）步，否则转第（6）步
3. 计算 a 的比特长度与 b 的比特长度之差，并将运算结果赋值给 rec
4. 将 a 与 b 左移 rec 位后的值进行按位异或运算
5. 将 ans 与 1 左移 rec 位后的值进行按位或运算，转第（2）步
6. 输出 ans，算法结束

4.2 流程图

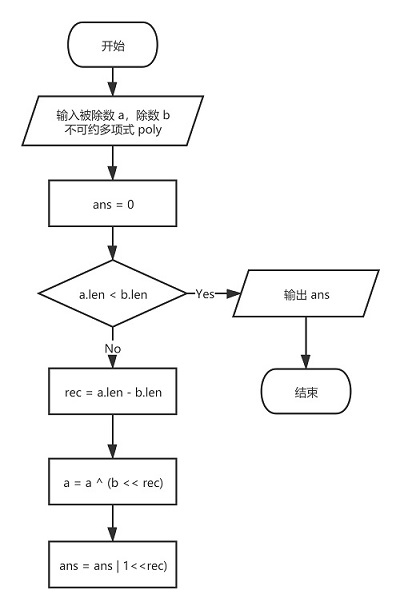
4.3 具体实现(python)

def gf2_divmod(a: int, b: int, poly: int) -> (int, int):
    """
    :param a: 被除数
    :param b: 除数
    :param poly: 不可约多项式
    :return: 商，余数
    """
    if b == 0:  # 除数不能为 0
        raise ZeroDivisionError
    ans = 0
    digit_a, digit_b = a.bit_length(), b.bit_length()
    while not a < b:
        rec = digit_a - digit_b
        a = a ^ (b << rec)
        ans = ans | (1 << rec)
        digit_a = a.bit_length()
    return ans, a

4.4 测试样例及结果

# 不可约多项式 poly = 0b100011011

0xde / 0xc6 = 0x01 ... 0x18
0x8c / 0x0a = 0x14 ... 0x04
0x3e / 0xa4 = 0x00 ... 0x3e

三、有限域数论算法

有限域的数论算法原理和实数域上的原理相同，此处仅给出代码，具体原理移步对应链接处

1. 有限域 GF(2ⁿ) 扩展欧几里得

https://www.cnblogs.com/kentle/p/14975039.html

1.1 具体实现

def gf2_ex_gcd(a: int, b: int, poly: int) -> (int, int, int):
    """
    :return: gcd x y
    """
    x1, y1, x2, y2 = 1, 0, 0, 1
    while b:
        q, r = gf2_divmod(a, b, poly)
        a, b = b, r
        x1, x2 = x2, x1 ^ gf2_mul(q, x2, poly)
        y1, y2 = y2, y1 ^ gf2_mul(q, y2, poly)
    return a, x1, y1

2. 有限域 GF(2ⁿ) 求逆

2.1 具体实现

def gf2_inverse(a: int, poly: int):
    """
    :param a: GF(2^n) 元素
    :param poly: 不可约多项式
    :return: a^(-1)
    """
    x1, x2 = 1, 0
    b = poly
    while b:
        q, r = gf2_divmod(a, b, poly)
        a, b = b, r
        x1, x2 = x2, x1 ^ gf2_mul(q, x2, poly)
    return x1

2.2 测试样例及结果

# 不可约多项式 poly = 0b100011011
iv(0x8c) = 0xf7 
iv(0xbe) = 0x86
iv(0x01) = 0x01
iv(0x2d) = 0x44

3. 有限域 GF(2ⁿ) 快速幂

https://www.cnblogs.com/kentle/p/14975044.html

3.1 具体实现

def gf2_quick_pow_mod(a: int, k: int, poly: int) -> int:
    """
    :return: a^k mod p
    """
    res = 1  # res: 计算结果
    while k:
        if k & 1:  # 如果 n 是奇数
            res = gf2_mul(res, a, poly)
        k = k // 2
        a = gf2_mul(a, a, poly)
    return res

四、用途

有限域 GF(2⁸) 常用于对称密码算法的构造，例如 AES 的列混淆和字节代替部分就使用了 GF(2⁸) 的有限域

参考资料：《密码学实验教程》