快速模幂

算法介绍

若要计算 a^k mod p，可先计算 a² mod p，a⁴ mod p，a⁸ mod p，...，再将 k 的二进制表示中等于 1 的位对应的 a 的幂相乘，便可得到结果，具体步骤如下：

1. 将 b 表示成二进制数 0 和 1 的字符串，令结果初始值为 1
2. 从 b 的最低位开始，若当前位为 1，则将当前结果乘以 a 模 p；若当前位为 0，则当前结果不变
3. 将 a 变为 a² mod p
4. 重复步骤（2）和步骤（3），直到 b 的每一位运算完毕，当前结果即为最终结果

算法流程图

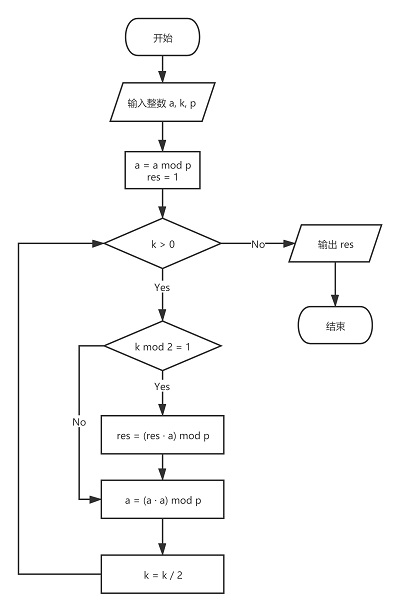
具体代码(python)

def quick_pow_mod(a: int, k: int, p: int) -> int:
    """
    :return: a^k mod p
    """
    a = a % p  # 避免 a 过大，先取一次模
    res = 1  # res: 计算结果
    while k:
        if k & 1:  # 如果 n 是奇数
            res = (res * a) % p
        k = k // 2
        a = (a * a) % p
    return res

测试样例及结果

# 样例一
a = 5
k = 1003
p = 31
# 结果 a^k mod p
res = 5

# 样例二
a = 1494462659429290047815067355171411187560751791530
k = 65537
p = 2268838711304724304304396119509416774597723292474
# 结果 a^k mod p
res = 2099538163720891467842744895846522520832379454230

最后

快速幂是一种思想，不一定只能用于整数的幂运算，在有限域（例如 GF2，椭圆曲线域）中的幂运算同样可以采用快速幂

如果是使用 python，在实际使用时建议使用自带的 pow 函数而不是自己写的快速模幂函数，因为 python 自带的 pow 效率要比自己写的要高得多

参考资料：《密码学实验教程》