扩展欧几里得算法

算法介绍

欧几里得算法（Euclid's Algorithm）又称辗转相除法。古希腊数学家欧几里得在其著作 The Elements 中最早描述了这种算法，所以该算法被命名为欧几里得算法。算法利用公式 gcd(a,b) = gcd(b, a mod b)，求两个非负整数 a 和 b 的最大公约数。欧几里得算法的具体步骤如下：

1. 若 b ≠ 0，使用带余除法，用 b 除以 a 得到余数 r；否则转到第（3）步
2. 用 b 代替 a, 用 r 代替 b，重复第（1）步
3. a 的值就是最大公约数 d

扩展欧几里得算法（Extend Euclid's Algorithm）是欧几里得算法的扩展，基于以下定理：对于任意两个整数 a, b，必存在整数 x, y，使得 xa + yb = gcd(a,b) 成立，求出整数解 x, y，可以得到 gcd(a,b)。扩展欧几里得算法具体步骤如下：

1. 定义 x1 = 1, y1 = 0, x2 = 0, y2 = 1
2. 若 b ≠ 0，使用带余除法，用 b 除以 a 得到余数 r；否则转到第（4）步
3. 用 b 代替 a, 用 r 代替 b， 令 x1, y1, x2, y2 = x2, y2, x1 - q·x2, y1 - q·y2，重复第（2）步
4. a 的值就是最大公约数 d，x1 和 y1 的值就是所求 x 和 y

扩展欧几里得原理

首先，有 \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} a \\ b \end{bmatrix}\)

令 \(q=[\frac{a}{b}]\)，即 q 为 \(a \div b\) 的整数部分，构建矩阵 \(\begin{bmatrix} 0 & 1 \\ 1 & -q \end{bmatrix}\)

将等式两端同时左乘上述矩阵，则有 \(\begin{bmatrix} 0 & 1 \\ 1 & -q \end{bmatrix} \cdot \begin{bmatrix} a\\b \end{bmatrix} = \begin{bmatrix} b \\ a-q \cdot b \end{bmatrix} = \begin{bmatrix} b \\ a \; mod \; b \end{bmatrix}\)

再令 \(q'=[\frac{b}{a \; mod \; b}]\)，重复上述步骤

最终有 \(\begin{bmatrix} x_1 & y_1 \\ x_2 & y_2 \end{bmatrix} \cdot \begin{bmatrix} a\\b \end{bmatrix} = \begin{bmatrix} gcd(a,b) \\ 0 \end{bmatrix}\)

即求出 \(x_1 \cdot a + y_1 \cdot b = gcd(a,b)\)

算法流程图

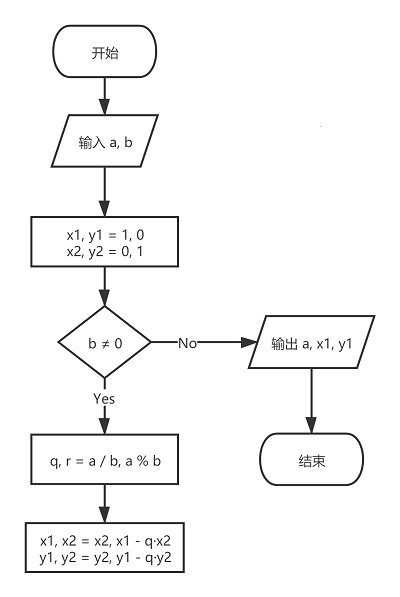
具体代码(python)

def ex_gcd(a: int, b: int) -> (int, int, int):
    """扩展欧几里得算法

    :return: gcd x y
    """
    # 0与0没有最大公约数，因为任何非零数都能整除 0
    if a == 0 and b == 0:
        return None
    else:
        x1, y1, x2, y2 = 1, 0, 0, 1  # 初始化x1,y1,x2,y2
        while b:
            q, r = divmod(a, b)
            a, b = b, r  # gcd(a,b)=gcd(b,a%b)
            # 下面操作模仿矩阵乘法，即
            # [[0,  1]    [[x1, y1]
            #  [1, -q]] x  [x2, y2]]
            x1, y1, x2, y2 = x2, y2, x1 - q * x2, y1 - q * y2
        # 返回一个三元组，依次是(gcd,x,y)，使得 xa+yb=gcd
        # 若传入的 a,b 是负数，那么最后结果有可能为负，需要取负
        return (a, x1, y1) if a > 0 else (-a, -x1, -y1)

测试样例和结果

# 样例一
a = 31
b = -13
# 结果 gcd = xa + yb
gcd = 1
x = -5
y = -12

# 样例二
a = 2461502723515673086658704256944912426065172925575
b = 1720876577542770214811199308823476528929542231719
# 结果 gcd = xa + yb
gcd = 1
x = -279503883787274514253902210297369853780943628056
y = 399795999407450264570090854758429065117844005679

# 样例三
a = 13709616469144948883512229123502305176385931810284088906755090238431898972708904439178898468021710798401875986657125211084472621499595371254346390738382042
b = 19235039994987625167590963480899777255933775238312044097122773255647530276806317636026727679800825370459321617724871515442147432420951257037823141069640181
# 结果 gcd = xa + yb
gcd = 1
x = -1076045803680437575165069317517720056816012968550552297497847522201869587140865136718292159497811949579872126471694232065112371318866682108000433819750738
y = 766942791672689226450200919445856853258490754050379704483194087100115700225755919066211027540484178869823084929299459228617007521725575705884841982026337

用途

在密码学中，互素是一个非常重要的概念，判断两个数互素就是计算其最大公约数是否为 1

同时，密码学中的逆元也是非常重要的概念，整数 e 在模数 p 下的逆元 d 需要满足 e·d mod p = 1。也就是 e·d + k·p = 1。使用扩展欧几里得算法计算 ex_gcd(e,p) 即可算出：如果结果的 gcd = 1，那么 x 就是 e 在模 p 下的逆元；如果结果的 gcd ≠ 1，那么表明 e 在模 p 下没有逆元

利用欧几里得求逆元

def inverse(n: int, p: int):
    """
    :return: n 在 mod p 下的逆元
    """
    gcd_, iv, _ = ex_gcd(n, p)
    if gcd_ != 1:
        raise ValueError(str(n) + " has no inverse in mod " + str(p))
    return iv % p

参考资料：《密码学实验教程》