使用 huffman 编码压缩与解压缩(python)
一、huffman 编码
1.1 huffman 编码介绍
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)
huffman 编码是最优码,也是即时码(证明较为复杂,在此不给出证明)
1.2 huffman 编码
此处介绍二元 huffman 编码
给定一个字符集合 \(S=\{s_0,s_1,\cdots,s_q\}\),每个字符的概率为 \(P=\{p_0,p_1,\cdots,p_q\}\)
-
将字符集合按概率由大到小重新排列,即使得 \(p_i ≥ p_{i+1}\)
-
将最末尾的两个字符 \(s_{q-1}\) 和 \(s_q\)合并,记为 \(s'\),\(s'\) 的概率为 \(p'=p_{q-1}+p_q\)
-
如果剩余的字符数不为 1,则回到第 1 步
huffman 编码的过程大致就上述三步
当编码完毕后,会构建出一棵码树,每个码字的编码可以从码树中获得
举个简单的例子,对于字符集合 \(S=\{A,B,C\}\),概率为 \(P={0.5,0.3,0.2}\)
-
将 \(B,C\) 合并,记为 \(BC\),\(p(BC)=p(B)+p(C)=0.3+0.2=0.5\)
-
然后将 \(A,BC\) 合并,记为 \(ABC\),\(p(ABC)=p(A)+p(BC)=0.5+0.5=1\)
记根节点 ABC 码字为空,从根节点向下遍历,往左走码字末尾添0,往右走添1,那么 A, B, C 的码字分别为 0, 10, 11,编码表就是 \(\{A:0,B:10,C:11\}\)
1.3 huffman 编程实现
见后文的代码实现
1.4 测试
首先在代码目录下新建一个newfile.txt,里边写入ABCDEFG
下面的代码实现了读取newfile.txt并对其压缩,将结果输出至output.enc
然后对output.enc进行解压缩,将解压缩结果输出至output.dec
# 读入文件
with open('newfile.txt', 'rb') as fp_in:
str_bytes = fp_in.read()
# 构建huffman编码
fre_dic = bytes_fre(str_bytes)
huffman_dic = build(fre_dic)
# 对文本进行编码
str_enc, padding = encode(str_bytes, huffman_dic, False)
# 输出至文件 output.enc
with open('output.enc', 'wb') as fp_out:
fp_out.write(str_enc)
# 对编码后的文本进行解码
str_dec = decode(str_enc, huffman_dic, padding, False)
# 输出至文件 output.dec
with open('output.dec', 'wb') as fp_out:
fp_out.write(str_dec)
# 打印huffman字典和填充位
print('huffman_dic:', huffman_dic)
print('padding:', padding)
观察压缩前和压缩后的文件,发现经过我们的程序压缩之后,文件小了很多
使用 winhex 打开 newfile.txt, output.enc, output.dec 查看对应的十六进制数值
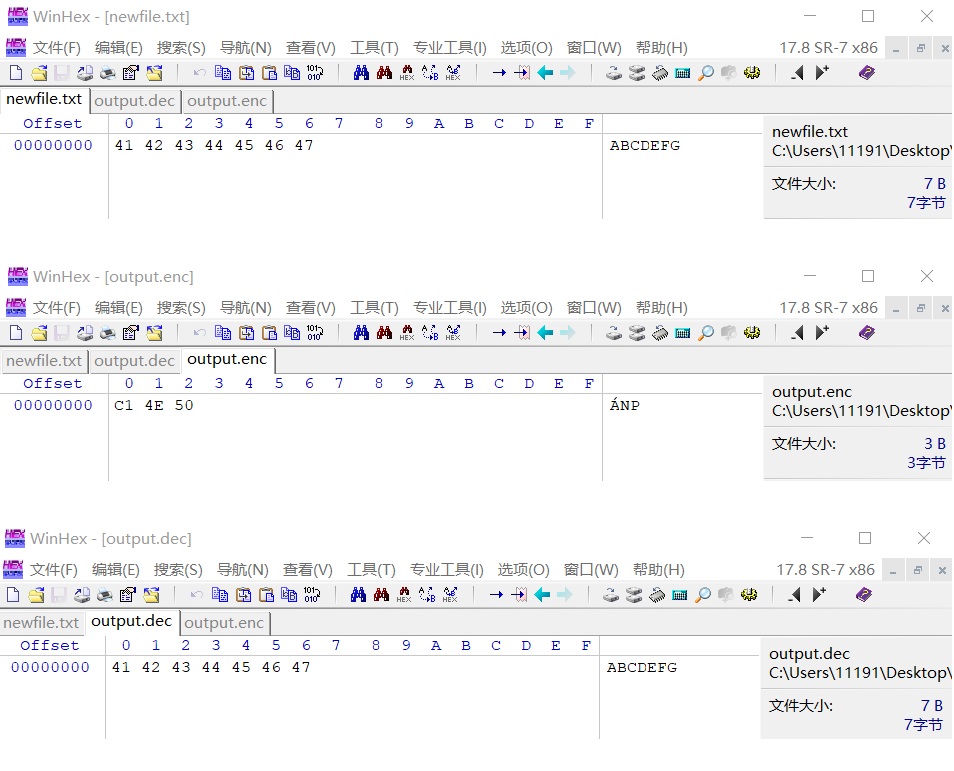
观察 newfile.txt 和 output.dec 的十六进制数值,发现一模一样,说明我们的压缩和解压并没有问题,程序正确
接下来来分析 output.enc 文件的内容
output.enc 中的数值为 C1 4E 50,转化成二进制为 11000001 01001110 01010000
我们将中间构造出的编码表打印出来,可以得到编码表
| 字符 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 编码 | 11 | 000 | 001 | 010 | 011 | 100 | 101 |
以及填充位 padding 的值为 4
我们对 newfile.txt 中的字符 ABCDEFG 进行编码,结果为 11 000 001 010 011 100 101。按 8 位二进制数一组划分后的结果为 11000001 01001110 0101,最后一组不满 8 位,需要补充 4 个 0,padding 值为 4,最后结果为 11000001 01001110 01010000,即 C1 4E 50
我们通过手算得出的编码输出和程序的编码输出一致!
说明程序正确!
二、利用 huffman 编码进行数据压缩
上面我们已经介绍了数据压缩的原理与最优码 huffman 编码,我们可以使用 huffman 编码对原先用 ASCII 码编码的数据重新编码,以达到数据压缩的目的
2.1 压缩
上面已经给出了 huffman 编码压缩的算法,而且也有很不错的压缩效率。但需要注意的是,无论是压缩的时候,还是解压的时候,我们都用到了从原文件中生成的 huffman 编码表和填充位数
思考一下我们平时的压缩软件,给它一个压缩包,它就能自动解压出原先的文件。但我们刚刚编写的程序似乎不行,它解码的时候需要用到一个编码表,而这个编码表只能从未编码的文件中获得,我们没办法只靠一个压缩后的文件就能恢复出源文件
那么,我们需要将编码表一并存入压缩文件中,在解压的时候读取编码表进行解压
2.2 码表存储
怎么存码表?这是一个非常复杂的问题。一个简单的方法是直接用明文存储,就像下图那样

事实上,根本不会有任何压缩软件采用这种方式存储码表,因为这占用非常大的存储空间。就拿上面的例子来说,一个 ASCII 字符占用 \(8\) 个二进制位,一共有 \(13\) 个字符,那么共占用了 \(8 \times 13 = 104\) 个二进制位!
看上去似乎并不大,但如果待编码字符数量增加到 256 个,最好的情况是每个码字都占用 \(8\) 个二进制位,那么存储码表需要 \(256 \times (8+8+8 \times 8) = 20480\) 个二进制位!也就是 \(\frac{20480}{8 \times 1024} = 2.5\) kb !
好吧,似乎看起来也不算太大,但它其实可以更小!
2.2.1 范式 huffman 编码
范式huffman编码对原先 huffman 编码的码树进行重构,使之变成具有特定规律的码树:位于码树同一层的码字,字典序小的靠左,字典序大的靠右,有后代的结点位于没有后代的结点的右侧
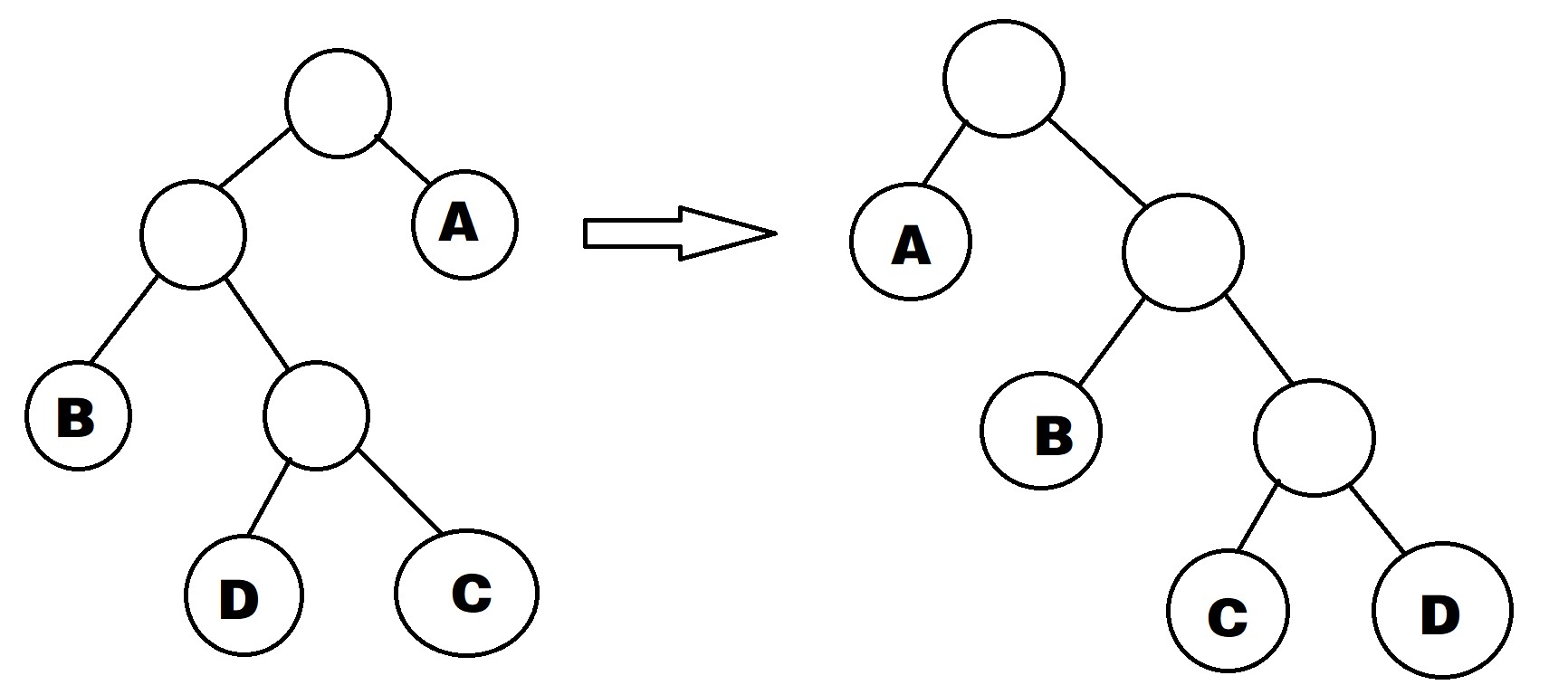
范式huffman 码字具有以下特点
-
将码树的码字由上至下,由左至右依次排列成 \(w_0,w_1,\cdots,w_n\)
-
对于同一层的码字,最左侧的码字总是形如 \(x\)0,之后的码字 \(w_i\) 都是其左侧码字的值加 1,即 \(w_i = w_{i-1} + 1\)
-
对于不在同一层的码字,设间隔层数为 \(d\),则 \(w_i = (w_{i-1}+1)\)0\(\cdots\)0 (\(d\)个\(0\))
以右图为例,\(A,B,C,D\) 四个字符对应的码字刚好符合上述特点
| 字符 | A | B | C | D |
|---|---|---|---|---|
| 码字 | 0 | 10 | 110 | 111 |
还原的时候,只需要知道字符序列 \(c_i\) 和对应的码字长度 \(l_i\),即可还原出最初的码字序列 \(w_i\)。根据码字长度可以确定出码字所在码树的层数,再结合 \(w_i\) 和 \(w_{i-1}\) 的递推关系,便可唯一确定码字序列
在构建 范式huffman 码表的时候,并不需要手动调节先前通过 huffman 编码所得的码树,只需要利用 huffman 编码所得到的码长序列,并按规则从新排列字符序列,传入 范式huffman 编码的构造函数之中,便可得到对应的码表
2.2.2 范式 huffman 的码表存储
|占用|1字节|1字节|m字节|n字节|x字节|
|-|-|-|-|-|-|-|
|含义|填充位数|最大码字长度m|\([1,m]\)长度的码字数量|字符序列|数据部分|
|记号|padding|m|length|char_lst|data|
通过读取 m 确定最大码字长度,后续的 m 个字节为 \([1,m]\) 长度的码字数目,进行处理可以获得码字长度序列 length_lst。对 length 求和可以获得字符个数 n,后续的 n 个字节为对应的字符序列 char_lst。通过 char_lst 和 length_lst 可以还原出码表
由于所有的字符数量为 256 个,最深码树深度为 255,故 m 并不会溢出(一个字节所能表示的数据范围为\([0,255]\))
但需要注意的是,若所有 256 个字符全部位于码树同一层,将无法用一个字节表示该层的码字数量。对于这种情况,将所有的码字数量全部置 0,即 length 全0;最大码字长度 m 不变。当检测到 length 全 0 但 m 不为 0 时,判断为 256 个字符全位于码树同一层的情况,将 length 最后一个数据修正为 256,继续后续操作
三、代码实现
3.1 一些函数
3.1.1 二进制与整数的转化
def int_to_bytes(n: int) -> bytes:
"""返回整数对应的二进制比特串 例如 50 -> b'\x50'"""
return bytes([n])
def bytes_to_int(b: bytes) -> int:
"""返回比特串对应的整数 例如 b'\x50' -> 50"""
return b[0]
3.1.2 压缩过程可视化
为了让我们能够看到压缩的进度,使用了 tqdm 库
tqdm 库可以打印出进度条,实时显示压缩与解压缩过程
需要注意,tqdm 库并不是 python 的自带库,需要通过 pip 或者 conda 安装
3.1.3 命令行参数
为了使我们的程序更方便他人调用,可以让其接收命令行的参数,从命令行中传入待压缩文件和输出路径,而不是通过修改代码中函数传入的文件路径
为此,python 的 argparse 库可以实现这个功能
需要注意,argparse 库并不是 python 的自带库,需要通过 pip 或者 conda 安装
3.2 基础 huffman 编码
为了使压缩过程可视化,需要导入 tqdm 库
为了让代码接口更为美观,需要导入 typing 库
from tqdm import tqdm
from typing import Dict, List, Tuple
3.2.1 频率统计
虽然在上面 huffman 编码的构造中使用的是字符的频率,但是由于计算机的精度问题,很可能会发生误差。所以此处采用的是频数来代替频率
def bytes_fre(bytes_str: bytes):
"""统计目标文本的字符频数, 返回频数字典
例如b'\x4F\x56\x4F' -> {b'\x4F':2, b'\x56':1}
"""
fre_dic = [0 for _ in range(256)]
for item in bytes_str:
fre_dic[item] += 1
return {int_to_bytes(x): fre_dic[x] for x in range(256) if fre_dic[x] != 0}
3.2.2 码表构建
首先先构造一个类,用于作为二叉树的结点
| 成员 | value | weight | lchild | rchild |
|---|---|---|---|---|
| 说明 | 具体的字符 | 字符的权重(频数) | 左孩子 | 右孩子 |
class Node:
"""Node结点,用于构建二叉数"""
def __init__(self, value, weight, lchild, rchild):
self.value = value
self.weight = weight
self.lchild = lchild
self.rchild = rchild
然后利用 Node 类构建 huffman 树,并生成 huffman 编码表
对于词频为空或者只有一个字符的情况,需要特殊考虑
def build(fre_dic: Dict[bytes, int]) -> Dict[bytes, str]:
"""通过字典构建Huffman编码,返回对应的编码字典
例如 {b'\x4F':1, b'\x56':1} -> {b'\x4F':'0', b'\x56':'1'}
"""
def dlr(current: Node, huffman_code: str, _huffman_dic: Dict[bytes, str]):
"""递归遍历二叉树求对应的Huffman编码"""
if current is None:
return
else:
if current.lchild is None and current.rchild is None:
_huffman_dic[current.value] = huffman_code
else:
dlr(current.lchild, huffman_code + '0', _huffman_dic)
dlr(current.rchild, huffman_code + '1', _huffman_dic)
if not fre_dic:
return {}
elif len(fre_dic) == 1:
return {value: '0' for value in fre_dic.keys()}
# 初始化森林, 权重weight小的在后
node_lst = [Node(value, weight, None, None) for value, weight in fre_dic.items()]
node_lst.sort(key=lambda item: item.weight, reverse=True)
# 构建Huffman树
while len(node_lst) > 1:
# 合并最后两棵树
node_2 = node_lst.pop()
node_1 = node_lst.pop()
node_add = Node(None, node_1.weight + node_2.weight, node_1, node_2)
node_lst.append(node_add)
# 调整森林
index = len(node_lst) - 1
while index and node_lst[index - 1].weight <= node_add.weight:
node_lst[index] = node_lst[index - 1]
index = index - 1
node_lst[index] = node_add
# 获取Huffman编码
huffman_dic = {key: '' for key in fre_dic.keys()}
dlr(node_lst[0], '', huffman_dic)
return huffman_dic
3.2.3 编码
def encode(str_bytes: bytes, huffman_dic: Dict[bytes, str], visualize: bool = False) -> Tuple[bytes, int]:
"""Huffman编码
输入待编码文本, Huffman字典huffman_dic
返回末端填充位数padding和编码后的文本
"""
bin_buffer = ''
padding = 0
# 生成整数->bytes的字典
dic = [int_to_bytes(item) for item in range(256)]
# 将bytes字符串转化成bytes列表
read_buffer = [dic[item] for item in str_bytes]
write_buffer = bytearray([])
# 循环读入数据,同时编码输出
for item in tqdm(read_buffer, unit='byte', disable=not visualize):
bin_buffer = bin_buffer + huffman_dic[item]
while len(bin_buffer) >= 8:
write_buffer.append(int(bin_buffer[:8:], 2))
bin_buffer = bin_buffer[8::]
# 将缓冲区内的数据填充后输出
if bin_buffer:
padding = 8 - len(bin_buffer)
bin_buffer = bin_buffer.ljust(8, '0')
write_buffer.append(int(bin_buffer, 2))
return bytes(write_buffer), padding
3.2.4 解码
def decode(str_bytes: bytes, huffman_dic: Dict[bytes, str], padding: int, visualize: bool = False):
"""Huffman解码
输入待编码文本, Huffman字典huffman_dic, 末端填充位padding
返回编码后的文本
"""
if not huffman_dic: # 空字典,直接返回
return b''
elif len(huffman_dic) == 1: # 字典长度为1,添加冗余结点,使之后续能够正常构建码树
huffman_dic[b'OVO'] = 'OVO'
# 初始化森林, 短码在前,长码在后, 长度相等的码字典序小的在前
node_lst = [Node(value, weight, None, None) for value, weight in huffman_dic.items()]
node_lst.sort(key=lambda _item: (len(_item.weight), _item.weight), reverse=False)
# 构建Huffman树
while len(node_lst) > 1:
# 合并最后两棵树
node_2 = node_lst.pop()
node_1 = node_lst.pop()
node_add = Node(None, node_1.weight[:-1:], node_1, node_2)
node_lst.append(node_add)
# 调整森林
node_lst.sort(key=lambda _item: (len(_item.weight), _item.weight), reverse=False)
# 解密文本
read_buffer, buffer_size = [], 0
# 生成字符->二进制列表的映射
dic = [list(map(int, bin(item)[2::].rjust(8, '0'))) for item in range(256)]
# 将str_bytes转化为二进制列表
for item in str_bytes:
read_buffer.extend(dic[item])
buffer_size = buffer_size + 8
read_buffer = read_buffer[0: buffer_size - padding:]
buffer_size = buffer_size - padding
write_buffer = bytearray([])
current = node_lst[0]
for pos in tqdm(range(0, buffer_size, 8), unit='byte', disable=not visualize):
for item in read_buffer[pos:pos + 8]:
# 根据二进制数移动current
if item:
current = current.rchild
else:
current = current.lchild
# 到达叶结点,打印字符并重置current
if current.lchild is None and current.rchild is None:
write_buffer.extend(current.value)
current = node_lst[0]
return bytes(write_buffer)
3.3 范式 huffman
3.3.1 码表的构造
def rebuild(char_lst: List[bytes], length_lst: List[int]) -> Dict[bytes, str]:
"""以范氏Huffman的形式恢复字典"""
huffman_dic = {value: '' for value in char_lst}
current_code = 0
for i in range(len(char_lst)):
if i == 0:
current_code = 0
else:
current_code = (current_code + 1) << (length_lst[i] - length_lst[i - 1])
huffman_dic[char_lst[i]] = bin(current_code)[2::].rjust(length_lst[i], '0')
return huffman_dic
3.3.2 普通huffman转范式huffman
def to_canonical(huffman_dic: Dict[bytes, str]) -> Dict[bytes, str]:
"""将Huffman编码转换成范氏Huffman编码"""
code_lst = [(value, len(code)) for value, code in huffman_dic.items()]
code_lst.sort(key=lambda item: (item[1], item[0]), reverse=False)
value_lst, length_lst = [], []
for value, length in code_lst:
value_lst.append(value)
length_lst.append(length)
return rebuild(value_lst, length_lst)
3.3.3 封装
将实现 范式huffman 功能的代码封装成 Huffman 类
| 函数名称 | 函数功能 | 返回值 |
|---|---|---|
| bytes_fre | 统计给定文本的词频 | 词频字典 |
| build | 给定词频字典构建 huffman 编码 | huffman 码表 |
| to_canonical | 将给定的 huffman 编码转化成 范式huffman 编码 | 范式huffman 编码的码表 |
| rebuild | 通过码表信息重构 范式huffman 编码 | 范式huffman 编码的码表 |
| encode | 使用给定码表对给定文本编码 | 编码后的文本 |
| decode | 使用给定码表对给定文本解码 | 解码后的文本 |
class Huffman:
"""Huffman编码"""
@staticmethod
def bytes_fre(bytes_str: bytes):
"""统计目标文本的字符频数, 返回频数字典
例如b'\x4F\x56\x4F' -> {b'\x4F':2, b'\x56':1}
"""
pass
@staticmethod
def build(fre_dic: Dict[bytes, int]) -> Dict[bytes, str]:
"""通过字典构建Huffman编码,返回对应的编码字典
例如 {b'\x4F':1, b'\x56':1} -> {b'\x4F':'0', b'\x56':'1'}
"""
pass
@classmethod
def to_canonical(cls, huffman_dic: Dict[bytes, str]) -> Dict[bytes, str]:
"""将Huffman编码转换成范氏Huffman编码"""
pass
@staticmethod
def rebuild(char_lst: List[bytes], length_lst: List[int]) -> Dict[bytes, str]:
"""以范氏Huffman的形式恢复字典"""
pass
@staticmethod
def decode(str_bytes: bytes, huffman_dic: Dict[bytes, str], padding: int, visualize: bool = False):
"""Huffman解码
输入待编码文本, Huffman字典huffman_dic, 末端填充位padding
返回编码后的文本
"""
pass
@staticmethod
def encode(str_bytes: bytes, huffman_dic: Dict[bytes, str], visualize: bool = False) -> Tuple[bytes, int]:
"""Huffman编码
输入待编码文本, Huffman字典huffman_dic
返回末端填充位数padding和编码后的文本
"""
pass
3.4 码表存储与恢复
将之前的 范式huffman 进一步封装,完成对码表的存储与恢复功能
然后对 Huffman 类进一步封装,封装成 OVO 类(名字乱起的
| 函数名称 | 函数功能 | 返回值 |
|---|---|---|
| encode | 对给定文件进行 huffman 编码 | 编码后的文件名 |
| decode | 对给定文件进行 huffman 解码 | 解码后的文件名 |
| encode_as_huffman | 对给定文本进行 huffman 编码 | 编码后的文本 |
| decode_as_huffman | 对给定文本进行 huffman 解码 | 解码后的文本 |
class OVO:
VERBOSE = 0b10 # -v 显示进度
@classmethod
def decode_as_huffman(cls, str_bytes: bytes, mode: int):
"""以huffman编码解码
输入byte串,返回解码后的byte串"""
padding = str_bytes[0]
max_length = str_bytes[1]
length = list(str_bytes[2:2 + max_length:])
char_num = sum(length)
# 如果length全零,那么表示256个字符全在同一层
if char_num == 0 and max_length != 0:
char_num = 256
length[max_length - 1] = 256
# 计算出还原huffman码表所需的信息
char_lst, length_lst = [], []
for pos in range(2 + max_length, 2 + max_length + char_num):
char_lst.append(int_to_bytes(str_bytes[pos]))
for i in range(max_length):
length_lst.extend([i + 1] * length[i])
# 重构码表
code_dic = Huffman.rebuild(char_lst, length_lst)
# huffman解码
str_bytes = str_bytes[2 + max_length + char_num::]
write_buffer = Huffman.decode(str_bytes, code_dic, padding, bool(mode & cls.VERBOSE))
return write_buffer
@classmethod
def encode_as_huffman(cls, str_bytes: bytes, mode: int):
"""以huffman编码的形式编码文件
输入bytes串,返回编码后的比特串"""
fre_dic = Huffman.bytes_fre(str_bytes)
code_dic = Huffman.build(fre_dic)
code_dic = Huffman.to_canonical(code_dic)
max_length = 0
for code in code_dic.values():
max_length = max(max_length, len(code))
length_lst = [0 for _ in range(max_length + 1)]
for code in code_dic.values():
length_lst[len(code)] += 1
# 要是256个字符全部位于同一层,使用全零标记
if length_lst[max_length] == 256:
length_lst[max_length] = 0
length_lst.pop(0) # 码长为0的字符并不存在,故删去
# 将码表信息转化成bytes类型
code_bytes = b''.join(code_dic.keys())
length_bytes = b''.join(map(int_to_bytes, length_lst))
# huffman编码
temp_buffer, padding = Huffman.encode(str_bytes, code_dic, bool(mode & cls.VERBOSE))
# 合并结果
code_data = int_to_bytes(max_length) + length_bytes + code_bytes
write_buffer = int_to_bytes(padding) + code_data + temp_buffer
return write_buffer
@classmethod
def decode(cls, source_path: str, target_path: str, mode: int = 0):
with open(source_path, 'rb') as fp_in:
with open(target_path, 'wb') as fp_out:
write_buffer = cls.decode_as_huffman(fp_in.read(), mode)
fp_out.write(write_buffer)
return target_path
@classmethod
def encode(cls, source_path: str, target_path: str, mode: int = 0):
with open(source_path, 'rb') as fp_in:
with open(target_path, 'wb') as fp_out:
write_buffer = cls.encode_as_huffman(fp_in.read(), mode)
fp_out.write(write_buffer)
return target_path
3.5 命令行调用
将上面的 Huffman 类和 OVO 类写在 OVO.py 文件内
3.5.1 压缩
在目录下创建 enc.py 文件,写入以下内容
命令行第一个参数是待压缩文件路径,第二个参数是压缩后的文件路径,-v参数是可选参数,添加-v后将会实时显示压缩进度
from OVO import OVO
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('source_path', type=str,
help='the file_path which you want to encode')
parser.add_argument('target_path', type=str, default=None,
help='the file_path which you want to output')
parser.add_argument('-v', '--verbose', help='increase output verbosity',
action='store_const', const=OVO.VERBOSE, default=0)
args = parser.parse_args()
mode = args.verbose
try:
res = OVO.encode(source_path=args.source_path, target_path=args.target_path, mode=mode)
print('\n{} has been encoded to {}'.format(args.source_path, res))
except FileNotFoundError as e:
print(e)
except OSError as e:
print(e)
print('check your path!')
except Exception as e:
print(e)
在调用时,我们只需要在控制台进入程序目录,输入 python enc.py newfile.txt output.enc 就可以实现对文件 newfile.txt 的压缩
3.5.2 解压
与压缩类似,在新建一个文件 dec.py,写入以下内容
from OVO import OVO
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('source_path', type=str,
help='the file_path which you want to encode')
parser.add_argument('target_path', type=str, default=None,
help='the file_path which you want to output')
parser.add_argument('-v', '--verbose', help='increase output verbosity',
action='store_const', const=OVO.VERBOSE, default=0)
args = parser.parse_args()
mode = args.verbose
try:
res = OVO.decode(source_path=args.source_path, target_path=args.target_path, mode=mode)
print('\n{} has been encoded to {}'.format(args.source_path, res))
except FileNotFoundError as e:
print(e)
except OSError as e:
print(e)
print('check your path!')
except Exception as e:
print(e)
在命令行输入 python dec.py output.enc output.dec 即可实现对文件 output.enc 的解压缩,解压结果位于 output.dec
3.5.3 效果
随便找一个大一点的文件(大约20M),然后使用我们的程序进行压缩
在这里使用了一张图片
输入 python enc.py ./test/pic.bmp output.enc -v
因为我的图片位于 ./test/pic.bmp,故第一个参数就是 ./test/pic.bmp;我想把压缩结果输出至当前目录下的 output.enc 文件中,故第二个参数就是 output.enc
然后添加 -v 参数,实时显示压缩进度

然后再对 output.enc 进行解压
输入 python dec.py output.enc pic_dec.bmp -v
因为我的压缩文件位于 output.enc,故第一个参数就是 output.enc;我想把解压结果输出至当前目录下的 pic_dec.bmp 文件中,故第二个参数就是 pic_dec.bmp
然后添加 -v 参数,实时显示压缩进度

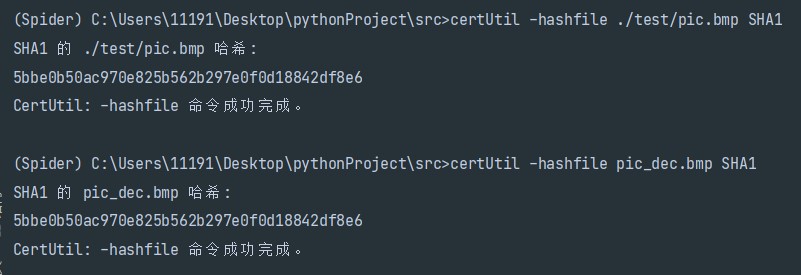
然后打开文件 pic_dec.bmp,可以正常打开!和之前的 pic.bmp 一模一样!程序正确!
不放心的话可以使用 winhex 检查16进制数值,或是通过命令certUtil -hashfile ./test/pic.bmp SHA1 和 certUtil -hashfile pic_dec.bmp SHA1 检查两个文件的 hash 值,一致的话就说明文件相同
3.6 完整代码
3.6.1 OVO.py
from tqdm import tqdm
from typing import Dict, List, Tuple
def int_to_bytes(n: int) -> bytes:
"""返回整数对应的二进制比特串 例如 50 -> b'\x50'"""
return bytes([n])
class Node:
"""Node结点,用于构建二叉数"""
def __init__(self, value, weight, lchild, rchild):
self.value = value
self.weight = weight
self.lchild = lchild
self.rchild = rchild
class Huffman:
"""Huffman编码"""
@staticmethod
def bytes_fre(bytes_str: bytes):
"""统计目标文本的字符频数, 返回频数字典
例如b'\x4F\x56\x4F' -> {b'\x4F':2, b'\x56':1}
"""
fre_dic = [0 for _ in range(256)]
for item in bytes_str:
fre_dic[item] += 1
return {int_to_bytes(x): fre_dic[x] for x in range(256) if fre_dic[x] != 0}
@staticmethod
def build(fre_dic: Dict[bytes, int]) -> Dict[bytes, str]:
"""通过字典构建Huffman编码,返回对应的编码字典
例如 {b'\x4F':1, b'\x56':1} -> {b'\x4F':'0', b'\x56':'1'}
"""
def dlr(current: Node, huffman_code: str, _huffman_dic: Dict[bytes, str]):
"""递归遍历二叉树求对应的Huffman编码"""
if current is None:
return
else:
if current.lchild is None and current.rchild is None:
_huffman_dic[current.value] = huffman_code
else:
dlr(current.lchild, huffman_code + '0', _huffman_dic)
dlr(current.rchild, huffman_code + '1', _huffman_dic)
if not fre_dic:
return {}
elif len(fre_dic) == 1:
return {value: '0' for value in fre_dic.keys()}
# 初始化森林, 权重weight小的在后
node_lst = [Node(value, weight, None, None) for value, weight in fre_dic.items()]
node_lst.sort(key=lambda item: item.weight, reverse=True)
# 构建Huffman树
while len(node_lst) > 1:
# 合并最后两棵树
node_2 = node_lst.pop()
node_1 = node_lst.pop()
node_add = Node(None, node_1.weight + node_2.weight, node_1, node_2)
node_lst.append(node_add)
# 调整森林
index = len(node_lst) - 1
while index and node_lst[index - 1].weight <= node_add.weight:
node_lst[index] = node_lst[index - 1]
index = index - 1
node_lst[index] = node_add
# 获取Huffman编码
huffman_dic = {key: '' for key in fre_dic.keys()}
dlr(node_lst[0], '', huffman_dic)
return huffman_dic
@classmethod
def to_canonical(cls, huffman_dic: Dict[bytes, str]) -> Dict[bytes, str]:
"""将Huffman编码转换成范氏Huffman编码"""
code_lst = [(value, len(code)) for value, code in huffman_dic.items()]
code_lst.sort(key=lambda item: (item[1], item[0]), reverse=False)
value_lst, length_lst = [], []
for value, length in code_lst:
value_lst.append(value)
length_lst.append(length)
return cls.rebuild(value_lst, length_lst)
@staticmethod
def rebuild(char_lst: List[bytes], length_lst: List[int]) -> Dict[bytes, str]:
"""以范氏Huffman的形式恢复字典"""
huffman_dic = {value: '' for value in char_lst}
current_code = 0
for i in range(len(char_lst)):
if i == 0:
current_code = 0
else:
current_code = (current_code + 1) << (length_lst[i] - length_lst[i - 1])
huffman_dic[char_lst[i]] = bin(current_code)[2::].rjust(length_lst[i], '0')
return huffman_dic
@staticmethod
def decode(str_bytes: bytes, huffman_dic: Dict[bytes, str], padding: int, visualize: bool = False):
"""Huffman解码
输入待编码文本, Huffman字典huffman_dic, 末端填充位padding
返回编码后的文本
"""
if not huffman_dic: # 空字典,直接返回
return b''
elif len(huffman_dic) == 1: # 字典长度为1,添加冗余结点,使之后续能够正常构建码树
huffman_dic[b'OVO'] = 'OVO'
# 初始化森林, 短码在前,长码在后, 长度相等的码字典序小的在前
node_lst = [Node(value, weight, None, None) for value, weight in huffman_dic.items()]
node_lst.sort(key=lambda _item: (len(_item.weight), _item.weight), reverse=False)
# 构建Huffman树
while len(node_lst) > 1:
# 合并最后两棵树
node_2 = node_lst.pop()
node_1 = node_lst.pop()
node_add = Node(None, node_1.weight[:-1:], node_1, node_2)
node_lst.append(node_add)
# 调整森林
node_lst.sort(key=lambda _item: (len(_item.weight), _item.weight), reverse=False)
# 解密文本
read_buffer, buffer_size = [], 0
# 生成字符->二进制列表的映射
dic = [list(map(int, bin(item)[2::].rjust(8, '0'))) for item in range(256)]
# 将str_bytes转化为二进制列表
for item in str_bytes:
read_buffer.extend(dic[item])
buffer_size = buffer_size + 8
read_buffer = read_buffer[0: buffer_size - padding:]
buffer_size = buffer_size - padding
write_buffer = bytearray([])
current = node_lst[0]
for pos in tqdm(range(0, buffer_size, 8), unit='byte', disable=not visualize):
for item in read_buffer[pos:pos + 8]:
# 根据二进制数移动current
if item:
current = current.rchild
else:
current = current.lchild
# 到达叶结点,打印字符并重置current
if current.lchild is None and current.rchild is None:
write_buffer.extend(current.value)
current = node_lst[0]
return bytes(write_buffer)
@staticmethod
def encode(str_bytes: bytes, huffman_dic: Dict[bytes, str], visualize: bool = False) -> Tuple[bytes, int]:
"""Huffman编码
输入待编码文本, Huffman字典huffman_dic
返回末端填充位数padding和编码后的文本
"""
bin_buffer = ''
padding = 0
# 生成整数->bytes的字典
dic = [int_to_bytes(item) for item in range(256)]
# 将bytes字符串转化成bytes列表
read_buffer = [dic[item] for item in str_bytes]
write_buffer = bytearray([])
# 循环读入数据,同时编码输出
for item in tqdm(read_buffer, unit='byte', disable=not visualize):
bin_buffer = bin_buffer + huffman_dic[item]
while len(bin_buffer) >= 8:
write_buffer.append(int(bin_buffer[:8:], 2))
bin_buffer = bin_buffer[8::]
# 将缓冲区内的数据填充后输出
if bin_buffer:
padding = 8 - len(bin_buffer)
bin_buffer = bin_buffer.ljust(8, '0')
write_buffer.append(int(bin_buffer, 2))
return bytes(write_buffer), padding
class OVO:
VERBOSE = 0b10 # -v 显示进度
@classmethod
def decode_as_huffman(cls, str_bytes: bytes, mode: int):
"""以huffman编码解码
输入byte串,返回解码后的byte串"""
padding = str_bytes[0]
max_length = str_bytes[1]
length = list(str_bytes[2:2 + max_length:])
char_num = sum(length)
# 如果length全零,那么表示256个字符全在同一层
if char_num == 0 and max_length != 0:
char_num = 256
length[max_length - 1] = 256
# 计算出还原huffman码表所需的信息
char_lst, length_lst = [], []
for pos in range(2 + max_length, 2 + max_length + char_num):
char_lst.append(int_to_bytes(str_bytes[pos]))
for i in range(max_length):
length_lst.extend([i + 1] * length[i])
# 重构码表
code_dic = Huffman.rebuild(char_lst, length_lst)
# huffman解码
str_bytes = str_bytes[2 + max_length + char_num::]
write_buffer = Huffman.decode(str_bytes, code_dic, padding, bool(mode & cls.VERBOSE))
return write_buffer
@classmethod
def encode_as_huffman(cls, str_bytes: bytes, mode: int):
"""以huffman编码的形式编码文件
输入bytes串,返回编码后的比特串"""
fre_dic = Huffman.bytes_fre(str_bytes)
code_dic = Huffman.build(fre_dic)
code_dic = Huffman.to_canonical(code_dic)
max_length = 0
for code in code_dic.values():
max_length = max(max_length, len(code))
length_lst = [0 for _ in range(max_length + 1)]
for code in code_dic.values():
length_lst[len(code)] += 1
# 要是256个字符全部位于同一层,使用全零标记
if length_lst[max_length] == 256:
length_lst[max_length] = 0
length_lst.pop(0) # 码长为0的字符并不存在,故删去
# 将码表信息转化成bytes类型
code_bytes = b''.join(code_dic.keys())
length_bytes = b''.join(map(int_to_bytes, length_lst))
# huffman编码
temp_buffer, padding = Huffman.encode(str_bytes, code_dic, bool(mode & cls.VERBOSE))
# 合并结果
code_data = int_to_bytes(max_length) + length_bytes + code_bytes
write_buffer = int_to_bytes(padding) + code_data + temp_buffer
return write_buffer
@classmethod
def decode(cls, source_path: str, target_path: str, mode: int = 0):
with open(source_path, 'rb') as fp_in:
with open(target_path, 'wb') as fp_out:
write_buffer = cls.decode_as_huffman(fp_in.read(), mode)
fp_out.write(write_buffer)
return target_path
@classmethod
def encode(cls, source_path: str, target_path: str, mode: int = 0):
with open(source_path, 'rb') as fp_in:
with open(target_path, 'wb') as fp_out:
write_buffer = cls.encode_as_huffman(fp_in.read(), mode)
fp_out.write(write_buffer)
return target_path
3.6.2 enc.py
from OVO import OVO
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('source_path', type=str,
help='the file_path which you want to encode')
parser.add_argument('target_path', type=str, default=None,
help='the file_path which you want to output')
parser.add_argument('-v', '--verbose', help='increase output verbosity',
action='store_const', const=OVO.VERBOSE, default=0)
args = parser.parse_args()
mode = args.verbose
try:
res = OVO.encode(source_path=args.source_path, target_path=args.target_path, mode=mode)
print('\n{} has been encoded to {}'.format(args.source_path, res))
except FileNotFoundError as e:
print(e)
except OSError as e:
print(e)
print('check your path!')
except Exception as e:
print(e)
3.6.3 dec.py
from OVO import OVO
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('source_path', type=str,
help='the file_path which you want to encode')
parser.add_argument('target_path', type=str, default=None,
help='the file_path which you want to output')
parser.add_argument('-v', '--verbose', help='increase output verbosity',
action='store_const', const=OVO.VERBOSE, default=0)
args = parser.parse_args()
mode = args.verbose
try:
res = OVO.decode(source_path=args.source_path, target_path=args.target_path, mode=mode)
print('\n{} has been encoded to {}'.format(args.source_path, res))
except FileNotFoundError as e:
print(e)
except OSError as e:
print(e)
print('check your path!')
except Exception as e:
print(e)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号