SM4加密算法原理和简单实现(java)
(一) SM4 算法介绍
下文引自百度百科
SM4.0(原名SM4.0)是中华人民共和国政府采用的一种分组密码标准,由国家密码管理局于2012年3月21日发布。
相关标准为“GM/T 0002-2012《SM4分组密码算法》(原SM4分组密码算法)”。
SM4 文档:http://www.gmbz.org.cn/main/viewfile/20180108015408199368.html
(二) SM4 算法流程
SM4 算法主要包含异或、移位以及盒变换操作。它分为密钥拓展和加/解密两个模块,这两个模块的流程大同小异
其中,移位变换是指循环左移;盒变换是一个将8bit输入映射到8bit输出的变换,是一个固定的变换
下图是 SM4 的加解密(左)和密钥拓展(右)的流程图
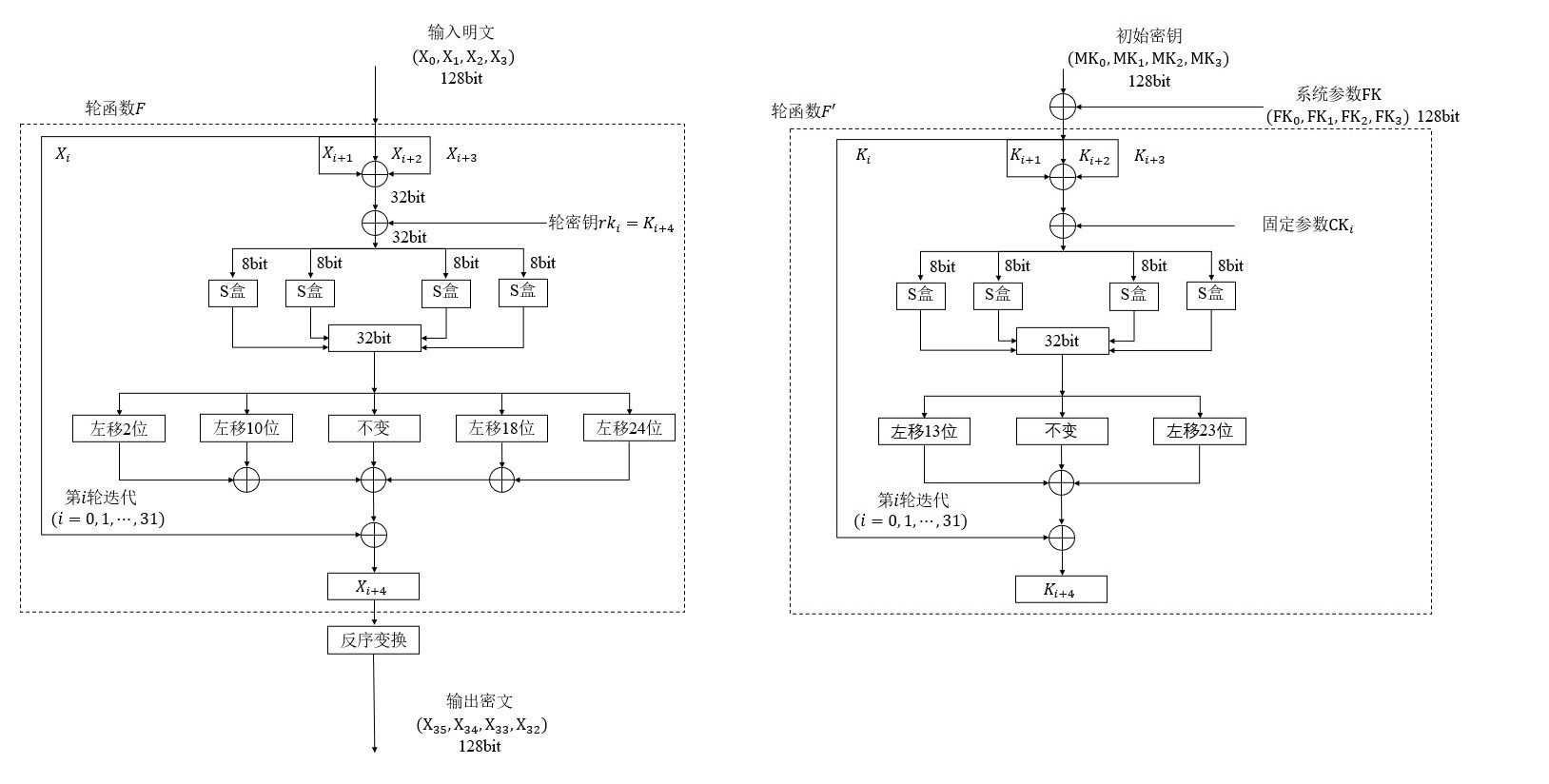
(1) 加解密
- 输入的明文为 128bit 的数据,将其按位拆分成 4 个 32bit 的数据 \(x_0,x_1,x_2,x_3\)
当 \(i=0\) 时为第一次轮变换,一直进行到 \(i=31\) 结束 - \(x_i\) 暂时不做处理,将 \(x_{i+1},x_{i+2},x_{i+3}\) 和轮密钥 \(rk_i\) 异或得到一个 32bit 的数据,作为盒变换的输入
即 \(sbox\_input= x_{i+1} \oplus x_{i+2} \oplus x_{i+3} \oplus rk_i\),\(\oplus\) 符号代表异或运算 - 将 \(sbox\_input\) 拆分成 4 个 8bit 数据,分别进行盒变换,之后再将 4 个 8bit 输出合并成一个 32bit 的 \(sbox\_output\)
- 将刚才获得的 \(sbox\_output\) 分别循环左移 2,10,18,24 位,得到 4 个 32bit 的结果,记移位结果为 \(y_2,y_{10},y_{18},y_{24}\)
- 将移位的结果 \(y_2,y_{10},y_{18},y_{24}\) 与盒变换输出 \(sbox\_output\) 和 \(x_i\) 异或,得到 \(x_{i+4}\)
即 \(x_{i+4}=sbox\_output \oplus y_2 \oplus y_{10} \oplus y_{18} \oplus y_{24} \oplus x_i\) - 至此完成了一轮的加解密运算
在实际加解密过程中,上述运算要执行 32 轮,同时使用 32 个不同的 \(rk_i\),\(rk_i\) 由密钥拓展生成 - 最后将生成的最后 4 个 32bit 数据 \(x_{35},x_{34},x_{33},x_{32}\) 合并成一个 128bit 的数据 \(output\),作为最后的输出结果
(2) 密钥拓展
- 密钥拓展的过程和加解密大同小异
- 输入的原始密钥 \(key\) 为 128bit 的数据,将其按位拆分成 4 个 \(32\)bit 的数据 \(K_0,K_1,K_2,K_3\)
- 将初始密钥 \(K_0,K_1,K_2,K_3\) 分别异或固定参数 \(FK_0,FK_1,FK_2,FK_3\) 得到用于循环的密钥 \(k_0,k_1,k_2,k_3\)
即 \(k_0=K_0 \oplus FK_0, k_1=K_1 \oplus FK_1, k_2=K_2 \oplus FK_2, k_3=K_3 \oplus FK_3\) - 进入轮密钥 \(rk_i\) 的生成
当 \(i=0\) 时为第一次轮变换,一直进行到 \(i=31\) 结束 - \(k_i\) 暂时不做处理,将 \(k_{i+1},k_{i+2},k_{i+3}\) 和固定参数 \(CK_i\) 异或得到一个 32bit 的数据,作为盒变换的输入
即 \(sbox\_input=k_{i+1} \oplus k_{i+2} \oplus k_{i+3} \oplus ck_i\) - 将 \(sbox\_input\) 拆分成 4 个 8bit 数据,分别进行盒变换,之后再将 4 个 8bit 输出合并成一个 32bit 的 \(sbox\_output\)
- 将刚才获得的 \(sbox\_output\) 分别循环左移 13,23 位,得到 2 个 32bit 的结果,记移位结果为 \(y_{13},y_{23}\)
- 将移位的结果 \(y_{13},y_{23}\) 与盒变换输出 \(sbox\_output\) 和 \(k_i\) 异或,得到 \(k_{i+4}\)
即 \(rk_i=k_{i+4}=sbox\_output \oplus y_{13} \oplus y_{23} \oplus k_i\) - 至此完成了一轮的加解密运算
在实际加解密过程中,上述运算要执行 32 轮,同时使用 32 个不同的 \(CK_i\),\(CK_i\) 为固定参数 - 执行完 32 轮后,便可获得 32 个用于加解密的 \(rk_i\)
(3) SM4 的逆运算
上文介绍了 SM4 的加密和密钥拓展部分,如果想要实现解密,一个简单的方法是将轮密钥 \(rk_i\) 逆序后再执行一次 32 轮的加密运算
即将密文投入加密函数,并且第 0 轮使用 \(rk_{31}\) 作为轮密钥,第 i 轮使用 \(rk_{31-i}\) 作为轮密钥,最后获得的结果便是加密前的密文
3.1 SM4 加密流程
先观察一下 SM4 加密的结构
-
令 SM4 的轮函数 \(F(x_i,x_{i+1},x_{i+2},x_{i+3},rk_i) = x_i \oplus T(x_{i+1} \oplus x_{i+2} \oplus x_{i+3} \oplus rk_i)\),其中函数 \(T\) 包括上述提到的盒变换和移位异或运算。那么 \(x_{i+4} = F(x_i,x_{i+1},x_{i+2},x_{i+3},rk_i)\)
-
以最后一轮加密运算为例,\(x_{35} = x_{31} \oplus T(x_{32} \oplus x_{33} \oplus x_{34} \oplus rk_{31})\),得到的 4 个 32 bit 字为 \(x_{32},x_{33},x_{34},x_{35}\)。最后输出会将这 4 个字逆序,即输出 \(x_{35},x_{34},x_{33},x_{32}\)
3.2 SM4 解密流程
接下来看解密,记加密的明文为 \(x_0, x_1, x_2, x_3\),将加密算法最后输出结果 \(x_{35}, x_{34}, x_{33}, x_{32}\) 记为 \(x_0', x_1', x_2',x_3'\),并让 \(rk_i' = rk_{31-i}\) (也就是轮密钥逆序)
将 \(x_0', x_1', x_2',x_3'\) 和 \(rk'_i\) 投入加密算法中,观察会发生什么结果
- 对于第 0 轮生成的 \(x_4' = x_0' \oplus T(x_1' \oplus x_2' \oplus x_3' \oplus rk_0')\),我们知道 \(x_0' = x_{35}, x_1' = x_{34}, x_2' = x_{33}, x_3' = x_{32}\),故 \(x_4' = x_{35} \oplus T(x_{34} \oplus x_{33} \oplus x_{32} \oplus rk_{31}) = x_{31} \oplus T(\cdots) \oplus T(\cdots) = x_{31}\)
- 类似的,我们可以得出 \(x_i' = x_{35-i}\),最后一轮函数结束后的结果为 \(x_3,x_2,x_1,x_0\),经过逆序后便是 \(x_0,x_1,x_2,x_3\),刚好是加密前的明文,完成了解密操作
通过 SM4 逆运算的过程,我们可以体会到 SM4 最后将结果逆序输出的巧妙之处
(三) SM4的java简单实现
需要注意的是,此处仅将 SM4 简单实现,而实际运用的时候,还需考虑各种工作模式(例如 OFB 或是 CFB)以及输入分组长度不是 128bit 的整数倍时需要添加的填充(例如 PKCS #7)。此处的代码仅用于展示 SM4 加解密过程的原理,输入的加密数据长度仅支持 128bit(长度为 16 的 byte 数组)
3.1 循环移位
在 java 中,移位操作符有 3 种,分别为 <<(左移),>>(算数右移)和 >>>(无符号右移)
其中,<< 是将 2 进制数整体左移一位,原先最高位舍弃,变为原先的次高位,最低位补 0
而 >> 是将 2 进制数整体右移一位,原先最低位舍弃,变为原先的次低位,最高位与原先最高位相同,效果类似于除 2
但 >>> 是将 2 进制数整体右移一位,原先最低位舍弃,变为原先的次低位,最高位补 0
在此我们使用的是 << 和 >>>
代码如下,非常简洁
/* 将input左移n位 */
private static int shift(int input, int n) {
return (input >>> (32 - n)) | (input << n);
}
3.2 将一个 32bit 数拆分成 4 个 8bit 数
/* 将32比特数拆分成4个8比特数 */
private static byte[] splitInt(int n) {
return new byte[]{(byte) (n >>> 24), (byte) (n >>> 16), (byte) (n >>> 8), (byte) n};
}
3.3 将 4 个 8bit 数合并为 1 个 32bit 数
此方法的是把 4 个 8bit 数合并为 1 个 32bit 数,输入 4 个 byte 类型,输出一个 int 类型
需要注意的是,因为 byte 类型存在符号位,对于 byte 的左移操作,倘若 byte 为负数,那么左移结果和我们想象的会不太一样。例如我们希望 0xFF 左移 8 位的结果为 0x0000FF00,但实际上结果却是 0xFFFFFF00
byte b = (byte)0xFF;
System.out.printf("%08x", b<<8);//0xffffff00
这是因为在 byte 类型左移时,会先转化成 int 类型,但由于符号位的原因,0xFF 会被转化成 0xFFFFFFFF(扩大的部分用符号位填充),导致结果与预期不同
为了抵消掉符号位的影响,我们可以先 与 上 0xFF。在进行 与 运算时,byte 类型同样会先转化成 int 类型,但我们只取其最低的 8 位,其余位置 0,便可抵消符号位的影响
/* 将4个8比特数合并成32比特数 */
private static int jointBytes(byte byte_0, byte byte_1, byte byte_2, byte byte_3) {
return ((byte_0 & 0xFF) << 24) | ((byte_1 & 0xFF) << 16) | ((byte_2 & 0xFF) << 8) | (byte_3 & 0xFF);
}
3.4 盒变换
S 盒实际上是一个 8 比特到 8 比特的映射。S 盒为 \(16 \times 16\) 的表格,输入的 8 比特数的前 4 比特确定行,后 4 比特确定列,行和列共同确定表格中的一项
下表是盒变换对应的表格(遇到表格显示不全时请缩放浏览器页面)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0xd6 | 0x90 | 0xe9 | 0xfe | 0xcc | 0xe1 | 0x3d | 0xb7 | 0x16 | 0xb6 | 0x14 | 0xc2 | 0x28 | 0xfb | 0x2c | 0x05 |
| 1 | 0x2b | 0x67 | 0x9a | 0x76 | 0x2a | 0xbe | 0x04 | 0xc3 | 0xaa | 0x44 | 0x13 | 0x26 | 0x49 | 0x86 | 0x06 | 0x99 |
| 2 | 0x9c | 0x42 | 0x50 | 0xf4 | 0x91 | 0xef | 0x98 | 0x7a | 0x33 | 0x54 | 0x0b | 0x43 | 0xed | 0xcf | 0xac | 0x62 |
| 3 | 0xe4 | 0xb3 | 0x1c | 0xa9 | 0xc9 | 0x08 | 0xe8 | 0x95 | 0x80 | 0xdf | 0x94 | 0xfa | 0x75 | 0x8f | 0x3f | 0xa6 |
| 4 | 0x47 | 0x07 | 0xa7 | 0xfc | 0xf3 | 0x73 | 0x17 | 0xba | 0x83 | 0x59 | 0x3c | 0x19 | 0xe6 | 0x85 | 0x4f | 0xa8 |
| 5 | 0x68 | 0x6b | 0x81 | 0xb2 | 0x71 | 0x64 | 0xda | 0x8b | 0xf8 | 0xeb | 0x0f | 0x4b | 0x70 | 0x56 | 0x9d | 0x35 |
| 6 | 0x1e | 0x24 | 0x0e | 0x5e | 0x63 | 0x58 | 0xd1 | 0xa2 | 0x25 | 0x22 | 0x7c | 0x3b | 0x01 | 0x21 | 0x78 | 0x87 |
| 7 | 0xd4 | 0x00 | 0x46 | 0x57 | 0x9f | 0xd3 | 0x27 | 0x52 | 0x4c | 0x36 | 0x02 | 0xe7 | 0xa0 | 0xc4 | 0xc8 | 0x9e |
| 8 | 0xea | 0xbf | 0x8a | 0xd2 | 0x40 | 0xc7 | 0x38 | 0xb5 | 0xa3 | 0xf7 | 0xf2 | 0xce | 0xf9 | 0x61 | 0x15 | 0xa1 |
| 9 | 0xe0 | 0xae | 0x5d | 0xa4 | 0x9b | 0x34 | 0x1a | 0x55 | 0xad | 0x93 | 0x32 | 0x30 | 0xf5 | 0x8c | 0xb1 | 0xe3 |
| a | 0x1d | 0xf6 | 0xe2 | 0x2e | 0x82 | 0x66 | 0xca | 0x60 | 0xc0 | 0x29 | 0x23 | 0xab | 0x0d | 0x53 | 0x4e | 0x6f |
| b | 0xd5 | 0xdb | 0x37 | 0x45 | 0xde | 0xfd | 0x8e | 0x2f | 0x03 | 0xff | 0x6a | 0x72 | 0x6d | 0x6c | 0x5b | 0x51 |
| c | 0x8d | 0x1b | 0xaf | 0x92 | 0xbb | 0xdd | 0xbc | 0x7f | 0x11 | 0xd9 | 0x5c | 0x41 | 0x1f | 0x10 | 0x5a | 0xd8 |
| d | 0x0a | 0xc1 | 0x31 | 0x88 | 0xa5 | 0xcd | 0x7b | 0xbd | 0x2d | 0x74 | 0xd0 | 0x12 | 0xb8 | 0xe5 | 0xb4 | 0xb0 |
| e | 0x89 | 0x69 | 0x97 | 0x4a | 0x0c | 0x96 | 0x77 | 0x7e | 0x65 | 0xb9 | 0xf1 | 0x09 | 0xc5 | 0x6e | 0xc6 | 0x84 |
| f | 0x18 | 0xf0 | 0x7d | 0xec | 0x3a | 0xdc | 0x4d | 0x20 | 0x79 | 0xee | 0x5f | 0x3e | 0xd7 | 0xcb | 0x39 | 0x48 |
- 例如 sbox(13)=0x76
实际上,我们并不需要特地将 S盒 设置成 \(16 \times 16\) 的二维数组,可以直接设置成长度为 \(256\) 的一维数组,就不需要拆分 8 比特确定行和列了
/* S盒变换 */
private static int sBox(int box_input) {
//s盒的参数
final int[] SBOX = {
0xD6, 0x90, 0xE9, 0xFE, 0xCC, 0xE1, 0x3D, 0xB7, 0x16, 0xB6, 0x14, 0xC2, 0x28, 0xFB, 0x2C, 0x05, 0x2B, 0x67, 0x9A,
0x76, 0x2A, 0xBE, 0x04, 0xC3, 0xAA, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99, 0x9C, 0x42, 0x50, 0xF4, 0x91, 0xEF,
0x98, 0x7A, 0x33, 0x54, 0x0B, 0x43, 0xED, 0xCF, 0xAC, 0x62, 0xE4, 0xB3, 0x1C, 0xA9, 0xC9, 0x08, 0xE8, 0x95, 0x80,
0xDF, 0x94, 0xFA, 0x75, 0x8F, 0x3F, 0xA6, 0x47, 0x07, 0xA7, 0xFC, 0xF3, 0x73, 0x17, 0xBA, 0x83, 0x59, 0x3C, 0x19,
0xE6, 0x85, 0x4F, 0xA8, 0x68, 0x6B, 0x81, 0xB2, 0x71, 0x64, 0xDA, 0x8B, 0xF8, 0xEB, 0x0F, 0x4B, 0x70, 0x56, 0x9D,
0x35, 0x1E, 0x24, 0x0E, 0x5E, 0x63, 0x58, 0xD1, 0xA2, 0x25, 0x22, 0x7C, 0x3B, 0x01, 0x21, 0x78, 0x87, 0xD4, 0x00,
0x46, 0x57, 0x9F, 0xD3, 0x27, 0x52, 0x4C, 0x36, 0x02, 0xE7, 0xA0, 0xC4, 0xC8, 0x9E, 0xEA, 0xBF, 0x8A, 0xD2, 0x40,
0xC7, 0x38, 0xB5, 0xA3, 0xF7, 0xF2, 0xCE, 0xF9, 0x61, 0x15, 0xA1, 0xE0, 0xAE, 0x5D, 0xA4, 0x9B, 0x34, 0x1A, 0x55,
0xAD, 0x93, 0x32, 0x30, 0xF5, 0x8C, 0xB1, 0xE3, 0x1D, 0xF6, 0xE2, 0x2E, 0x82, 0x66, 0xCA, 0x60, 0xC0, 0x29, 0x23,
0xAB, 0x0D, 0x53, 0x4E, 0x6F, 0xD5, 0xDB, 0x37, 0x45, 0xDE, 0xFD, 0x8E, 0x2F, 0x03, 0xFF, 0x6A, 0x72, 0x6D, 0x6C,
0x5B, 0x51, 0x8D, 0x1B, 0xAF, 0x92, 0xBB, 0xDD, 0xBC, 0x7F, 0x11, 0xD9, 0x5C, 0x41, 0x1F, 0x10, 0x5A, 0xD8, 0x0A,
0xC1, 0x31, 0x88, 0xA5, 0xCD, 0x7B, 0xBD, 0x2D, 0x74, 0xD0, 0x12, 0xB8, 0xE5, 0xB4, 0xB0, 0x89, 0x69, 0x97, 0x4A,
0x0C, 0x96, 0x77, 0x7E, 0x65, 0xB9, 0xF1, 0x09, 0xC5, 0x6E, 0xC6, 0x84, 0x18, 0xF0, 0x7D, 0xEC, 0x3A, 0xDC, 0x4D,
0x20, 0x79, 0xEE, 0x5F, 0x3E, 0xD7, 0xCB, 0x39, 0x48
};
byte[] temp = splitInt(box_input);//拆分32比特数
byte[] output = new byte[4];//单个盒变换输出
//盒变换
for (int i = 0; i < 4; i++) {
output[i] = (byte) SBOX[temp[i] & 0xFF];
}
//将4个8位字节合并为一个字作为盒变换输出
return jointBytes(output[0], output[1], output[2], output[3]);
}
3.5 加解密主函数
这个函数输入的是 byte 数组,输出也是 byte 数组。byte 只有 8 位,而加解密过程我们是以 32bit,即 int 类型为单位运算的,故先要把 byte 数组合并成 int 数组
最后函数输出的是 byte 类型数组,同样的,需要把最后 int 类型的结果转化成 byte
/* 加解密主模块 */
private static byte[] sm4Main(byte[] input, int[] key_r, int mod) {
int[] text = new int[4];//32比特字
//将输入以32比特分组
for (int i = 0; i < 4; i++) {
text[i] = jointBytes(input[4 * i], input[4 * i + 1], input[4 * i + 2], input[4 * i + 3]);
}
int box_input, box_output;//盒变换输入和输出
for (int i = 0; i < 32; i++) {
int index = (mod == 0) ? i : (31 - i);//通过改变key_r的顺序改变模式
box_input = text[1] ^ text[2] ^ text[3] ^ key_r[index];
box_output = sBox(box_input);
int temp = text[0] ^ box_output ^ shift(box_output, 2) ^ shift(box_output, 10) ^ shift(box_output, 18) ^ shift(box_output, 24);
text[0] = text[1];
text[1] = text[2];
text[2] = text[3];
text[3] = temp;
}
byte[] output = new byte[16];//输出
//将结果的32比特字逆序拆分
for (int i = 0; i < 4; i++) {
System.arraycopy(splitInt(text[3 - i]), 0, output, 4 * i, 4);
}
return output;
}
(四) 完整代码
public class SM4 {
int[] key_r;
/* 初始化轮密钥 */
SM4(byte[] key) {
this.key_r = keyGenerate(key);
}
/* 密钥拓展 */
private int[] keyGenerate(byte[] key) {
int[] key_r = new int[32];//轮密钥rk_i
int[] key_temp = new int[4];
int box_in, box_out;//盒变换输入输出
final int[] FK = {0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc};
final int[] CK = {
0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
};
//将输入的密钥每32比特合并,并异或FK
for (int i = 0; i < 4; i++) {
key_temp[i] = jointBytes(key[4 * i], key[4 * i + 1], key[4 * i + 2], key[4 * i + 3]);
key_temp[i] = key_temp[i] ^ FK[i];
}
//32轮密钥拓展
for (int i = 0; i < 32; i++) {
box_in = key_temp[1] ^ key_temp[2] ^ key_temp[3] ^ CK[i];
box_out = sBox(box_in);
key_r[i] = key_temp[0] ^ box_out ^ shift(box_out, 13) ^ shift(box_out, 23);
key_temp[0] = key_temp[1];
key_temp[1] = key_temp[2];
key_temp[2] = key_temp[3];
key_temp[3] = key_r[i];
}
return key_r;
}
/* 加解密主模块 */
private static byte[] sm4Main(byte[] input, int[] key_r, int mod) {
int[] text = new int[4];//32比特字
//将输入以32比特分组
for (int i = 0; i < 4; i++) {
text[i] = jointBytes(input[4 * i], input[4 * i + 1], input[4 * i + 2], input[4 * i + 3]);
}
int box_input, box_output;//盒变换输入和输出
for (int i = 0; i < 32; i++) {
int index = (mod == 0) ? i : (31 - i);//通过改变key_r的顺序改变模式
box_input = text[1] ^ text[2] ^ text[3] ^ key_r[index];
box_output = sBox(box_input);
int temp = text[0] ^ box_output ^ shift(box_output, 2) ^ shift(box_output, 10) ^ shift(box_output, 18) ^ shift(box_output, 24);
text[0] = text[1];
text[1] = text[2];
text[2] = text[3];
text[3] = temp;
}
byte[] output = new byte[16];//输出
//将结果的32比特字拆分
for (int i = 0; i < 4; i++) {
System.arraycopy(splitInt(text[3 - i]), 0, output, 4 * i, 4);
}
return output;
}
/* 加密 */
public byte[] encrypt(byte[] plaintext) {
return sm4Main(plaintext, key_r, 0);
}
/* 解密 */
public byte[] decrypt(byte[] ciphertext) {
return sm4Main(ciphertext, key_r, 1);
}
/* 将32比特数拆分成4个8比特数 */
private static byte[] splitInt(int n) {
return new byte[]{(byte) (n >>> 24), (byte) (n >>> 16), (byte) (n >>> 8), (byte) n};
}
/* 将4个8比特数合并成32比特数 */
private static int jointBytes(byte byte_0, byte byte_1, byte byte_2, byte byte_3) {
return ((byte_0 & 0xFF) << 24) | ((byte_1 & 0xFF) << 16) | ((byte_2 & 0xFF) << 8) | (byte_3 & 0xFF);
}
/* S盒变换 */
private static int sBox(int box_input) {
//s盒的参数
final int[] SBOX = {
0xD6, 0x90, 0xE9, 0xFE, 0xCC, 0xE1, 0x3D, 0xB7, 0x16, 0xB6, 0x14, 0xC2, 0x28, 0xFB, 0x2C, 0x05, 0x2B, 0x67, 0x9A,
0x76, 0x2A, 0xBE, 0x04, 0xC3, 0xAA, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99, 0x9C, 0x42, 0x50, 0xF4, 0x91, 0xEF,
0x98, 0x7A, 0x33, 0x54, 0x0B, 0x43, 0xED, 0xCF, 0xAC, 0x62, 0xE4, 0xB3, 0x1C, 0xA9, 0xC9, 0x08, 0xE8, 0x95, 0x80,
0xDF, 0x94, 0xFA, 0x75, 0x8F, 0x3F, 0xA6, 0x47, 0x07, 0xA7, 0xFC, 0xF3, 0x73, 0x17, 0xBA, 0x83, 0x59, 0x3C, 0x19,
0xE6, 0x85, 0x4F, 0xA8, 0x68, 0x6B, 0x81, 0xB2, 0x71, 0x64, 0xDA, 0x8B, 0xF8, 0xEB, 0x0F, 0x4B, 0x70, 0x56, 0x9D,
0x35, 0x1E, 0x24, 0x0E, 0x5E, 0x63, 0x58, 0xD1, 0xA2, 0x25, 0x22, 0x7C, 0x3B, 0x01, 0x21, 0x78, 0x87, 0xD4, 0x00,
0x46, 0x57, 0x9F, 0xD3, 0x27, 0x52, 0x4C, 0x36, 0x02, 0xE7, 0xA0, 0xC4, 0xC8, 0x9E, 0xEA, 0xBF, 0x8A, 0xD2, 0x40,
0xC7, 0x38, 0xB5, 0xA3, 0xF7, 0xF2, 0xCE, 0xF9, 0x61, 0x15, 0xA1, 0xE0, 0xAE, 0x5D, 0xA4, 0x9B, 0x34, 0x1A, 0x55,
0xAD, 0x93, 0x32, 0x30, 0xF5, 0x8C, 0xB1, 0xE3, 0x1D, 0xF6, 0xE2, 0x2E, 0x82, 0x66, 0xCA, 0x60, 0xC0, 0x29, 0x23,
0xAB, 0x0D, 0x53, 0x4E, 0x6F, 0xD5, 0xDB, 0x37, 0x45, 0xDE, 0xFD, 0x8E, 0x2F, 0x03, 0xFF, 0x6A, 0x72, 0x6D, 0x6C,
0x5B, 0x51, 0x8D, 0x1B, 0xAF, 0x92, 0xBB, 0xDD, 0xBC, 0x7F, 0x11, 0xD9, 0x5C, 0x41, 0x1F, 0x10, 0x5A, 0xD8, 0x0A,
0xC1, 0x31, 0x88, 0xA5, 0xCD, 0x7B, 0xBD, 0x2D, 0x74, 0xD0, 0x12, 0xB8, 0xE5, 0xB4, 0xB0, 0x89, 0x69, 0x97, 0x4A,
0x0C, 0x96, 0x77, 0x7E, 0x65, 0xB9, 0xF1, 0x09, 0xC5, 0x6E, 0xC6, 0x84, 0x18, 0xF0, 0x7D, 0xEC, 0x3A, 0xDC, 0x4D,
0x20, 0x79, 0xEE, 0x5F, 0x3E, 0xD7, 0xCB, 0x39, 0x48
};
byte[] temp = splitInt(box_input);//拆分32比特数
byte[] output = new byte[4];//单个盒变换输出
//盒变换
for (int i = 0; i < 4; i++) {
output[i] = (byte) SBOX[temp[i] & 0xFF];
}
//将4个8位字节合并为一个字作为盒变换输出
return jointBytes(output[0], output[1], output[2], output[3]);
}
/* 将input左移n位 */
private static int shift(int input, int n) {
return (input >>> (32 - n)) | (input << n);
}
}
(五) 代码正确性检验
为了验证自己实现的 SM4 代码是正确的,此处将加密结果与 Hutool 库的加密结果作比对,说明算法的正确性(SM4Test.java与SM4.java位于同一目录)
import cn.hutool.core.util.HexUtil;
import cn.hutool.crypto.SmUtil;
import cn.hutool.crypto.symmetric.SymmetricCrypto;
public class SM4Test {
public static void main(String[] args) {
// key必须是16位
byte[] key = "1234567812345678".getBytes();//128bit(16byte)
byte[] plaintext = "1234567812345678".getBytes();//128bit(16byte)
SymmetricCrypto sm4 = SmUtil.sm4(key);
byte[] ciphertext = sm4.encrypt(plaintext);//库加密结果
System.out.println("库函数加密结果\t\t" + new String(HexUtil.encodeHex(ciphertext)));
//e863652f50ad5ed9fcc038b25deb07101db94f833e5b4cf024c8f8d61d70d48c
SM4 sm4_t = new SM4(key);
byte[] ciphertext_t = sm4_t.encrypt(plaintext);//自己写的函数加密结果
System.out.println("自己写的函数加密结果\t" + new String(HexUtil.encodeHex(ciphertext_t)));
//e863652f50ad5ed9fcc038b25deb0710
byte[] res = sm4_t.decrypt(ciphertext_t);
System.out.println("加解密正确性\t\t\t" + new String(res).equals(new String(plaintext)));
//true
//byte[] padding = sm4_t.encrypt(HexUtil.decodeHex("10101010101010101010101010101010"));
//System.out.println("填充位数据加密结果\t\t" + new String(HexUtil.encodeHex(padding)));
//1db94f833e5b4cf024c8f8d61d70d48c
}
}
我们发现,Hutool 库的加密结果有 256bit(32字节),其中前 128bit(16字节) 和我们自己的函数加密结果一致。对于多出来的 128bit,是因为其采用了 PKCS #7 填充(应该是)
-
SM4 的加密分组为 16 字节,对于分组长度为 \(n\) 字节 的数据,其后续填充的长度为 \(16 - (n \; mod \; 16)\) 字节,填充的值为填充的字节数。需要注意的是,当数据分组长度恰好是加密分组长度的整数倍时,依旧需要填充
-
对于上述的数据,因为加密分组长度为 16 字节,根据
PKCS #7填充规则,需要填充 \(16 - (16 \; mod \; 16) = 16\) 字节的数据,数据内容为 16 (对应的十六进制数为 0x10)。故填充位数据用 16 进制字符串表示则为 16 个10
我们试着加密十六进制数据 10101010101010101010101010101010 (也就是把上面代码的后面部分解除注释),结果如下
byte[] padding = sm4_t.encrypt(HexUtil.decodeHex("10101010101010101010101010101010"));
System.out.println("填充位数据加密结果\t\t"+ new String(HexUtil.encodeHex(padding)));
//1db94f833e5b4cf024c8f8d61d70d48c
发现加密的结果就是库函数加密结果的后面 128bit,验证了 Hutool 的 SM4 采用了 PKCS #7 填充方式,同时也验证了我们自己写的函数能够实现 SM4 的加解密操作
突然发现 HuTool 可以设置不使用填充的 SM4,具体代码如下(小心和上面自己写的SM4发生命名冲突)
import cn.hutool.core.util.HexUtil;
import cn.hutool.crypto.Mode;
import cn.hutool.crypto.Padding;
import cn.hutool.crypto.symmetric.SM4;
public class SM4Test {
public static void main(String[] args) {
// key必须是16位
byte[] key = "1234567812345678".getBytes();//128bit(16byte)
byte[] plaintext = "1234567812345678".getBytes();//128bit(16byte)
SM4 sm4 = new SM4(Mode.ECB, Padding.NoPadding, key);
byte[] ciphertext = sm4.encrypt(plaintext);//库加密结果
System.out.println("库函数加密结果\t\t" + new String(HexUtil.encodeHex(ciphertext)));
//e863652f50ad5ed9fcc038b25deb07101db94f833e5b4cf024c8f8d61d70d48c
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号