DFT频谱分析实验

题述

　　有一调幅信号$x_\alpha (t)=[1+cos(2\pi \times 100t)]cos(2\pi \times 600t)$，用DFT做频谱分析，要求能分辨出$x_\alpha (t)$的所有频率分量。

 

 

理论分析

　　本题考察的是对时域采样和频域采样的理解。

　　对于时域采样，不失真的条件是$f_s > 2f_h$，即采样频率必须大于信号的最大频率分量；其次，我们还能得到数字频率量和模拟频率之间的关系：$\omega = \Omega T$，T为采样的时间间隔，该关系是由以下变换得到的：

$x_a(t)=Asin(\Omega t + \varphi ) \rightarrow  x(n)=Asin(\Omega nT + \varphi )=Asin(\omega n + \varphi )$

　　对于频域采样，DFT实际上是对Z域单位圆上的等间隔采样，假设输入的有限长序列长度为N，则采样间隔$\Delta \omega = \frac{2 \pi}{N}$。结合时域采样，可知DFT变换的结果$X(k)$各频率点对应的模拟频率为$\Omega = \frac{2 \pi k}{NT}$，频谱的分辨率为$\Delta f = \frac{1}{NT}$。

　　显然，如果时域信号里的有较大的频率分量，那么为了保证不失真，就要增大采样频率；但是这样一来会使得频谱分辨率变大，更多的频率分量会被忽略，所以必须增大序列长度N，也就是在时域采更多的点。

　　题目中的调幅信号可以简化为$x_\alpha (t)=cos(2\pi \times 600t) + \frac{1}{2}cos(2\pi \times 700t)+ \frac{1}{2}cos(2\pi \times 500t)$。最高频率为700Hz，那么采样频率需满足$f_s > 1.4kHz$，这里取$f_s = 3kHz$；因为信号最小的频率差是100Hz，于是可得$N > 30$。实验中一般选择2的幂次方，利用FFT加速计算。

 

 

 

实验结果

 

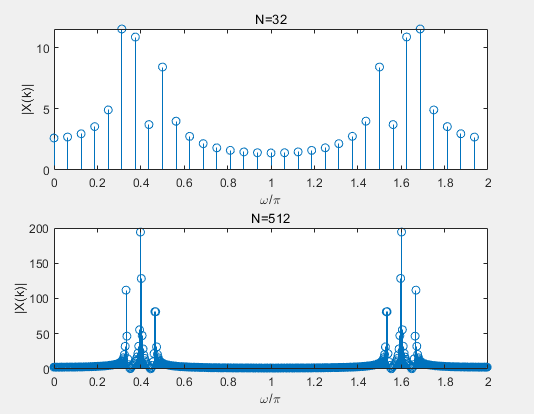
　　这里对比了N=32和N=512的两种情况，在N=32时，由于截断了较少的数据点，频谱发生了严重的泄露，导致其他分量上也出现了较大的幅值；N=512时，频域采样较密，结果更精确。

　　另外还应注意到，得到的两个频谱都关于$\omega = \pi$对称。事实上，由于采样条件$f_s > 2f_h$的限制，使得有效的数字频率$|\omega| = \Omega T \leq \frac{2\pi f_h}{f_s} \leq \pi$。也就是说，在$\omega = \pi$的附近是高频，而0和$2\pi$则是低频。有时候，$w=0 \sim \pi$的频谱就完全可以表示时域信号的频率特性，只是DFT是在$w=0 \sim 2\pi$上多采样了半个周期罢了。当然，有时候频谱并不是关于$\omega = \pi$对称的，还得看频域的采样点是否能取到$\omega = \pi$。