序列卷积:线性、周期和圆周
线性卷积
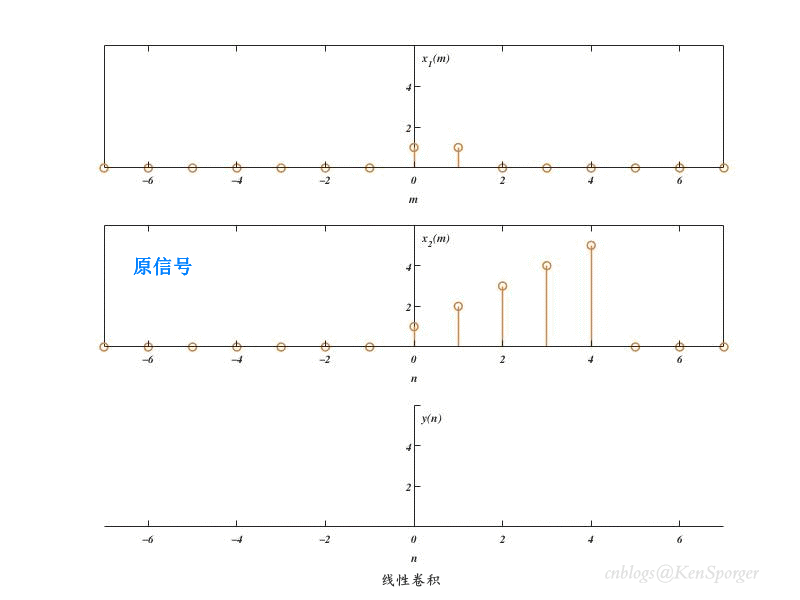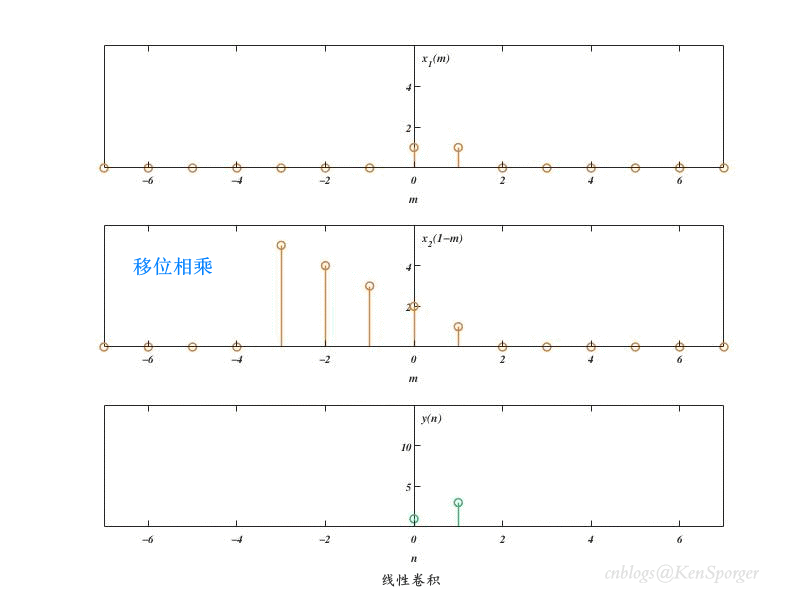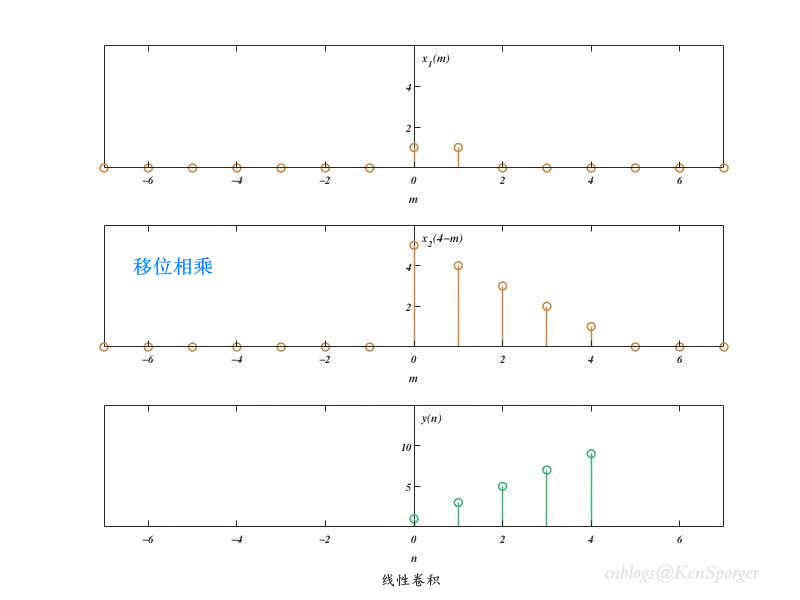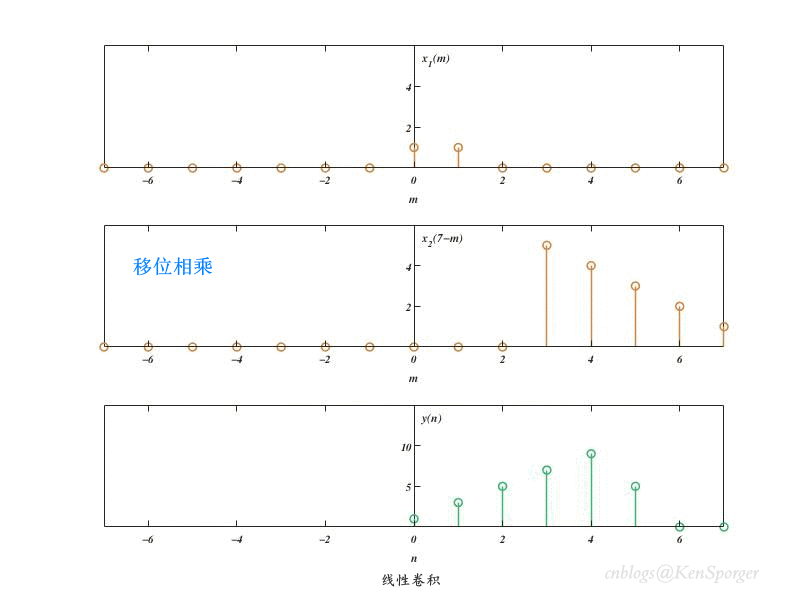
线性卷积公式为$y(n)=x_1(n) \ast x_2(n)= \sum_{m=-\infty}^{\infty} x_1(m)x_2(n-m) = \sum_{m=-\infty}^{\infty} x_2(m)x_1(n-m)$。
卷积的过程可以理解为其中一个序列关于Y轴翻褶,然后不断移位,同时与另外一个序列进行相乘。
周期卷积
周期为N的卷积公式为$\tilde{y}(n)=\sum_{m=0}^{N-1} \tilde{x_1}(m) \tilde{x_2}(n-m)$。
首先,两个输入都是周期为N的序列,卷积的方法与线性卷积类似,只是相乘时有效部分为m=0到N-1,即只在m=0到N-1上进行卷积。
N=10的周期卷积如下 ,可以看到卷积结果也是一个周期为N的序列。而且,$x_1(n)$的有效长度$N_1=2$,$x_2(n)$的有效长度$N_2=5$,而周期$N>N_1+N_2-1$,所以$\tilde{y}(n)$的主值序列与线性卷积结果是相同的。
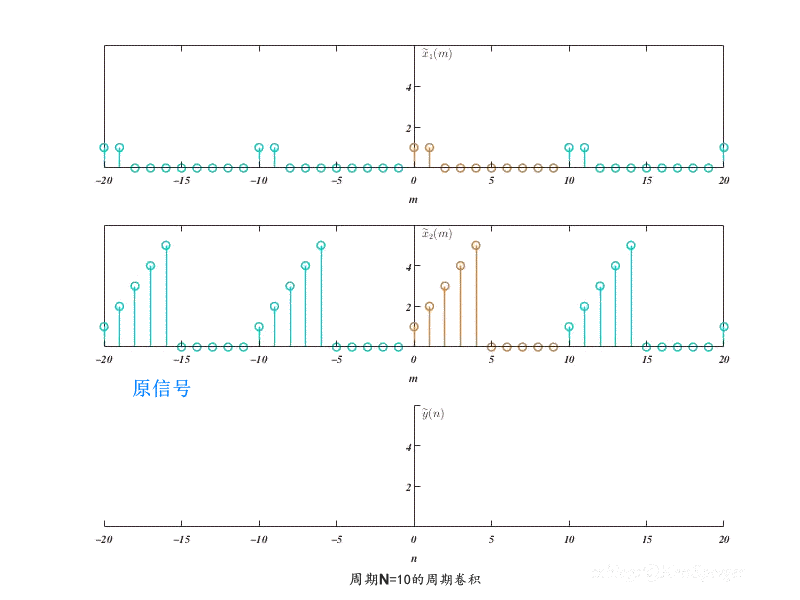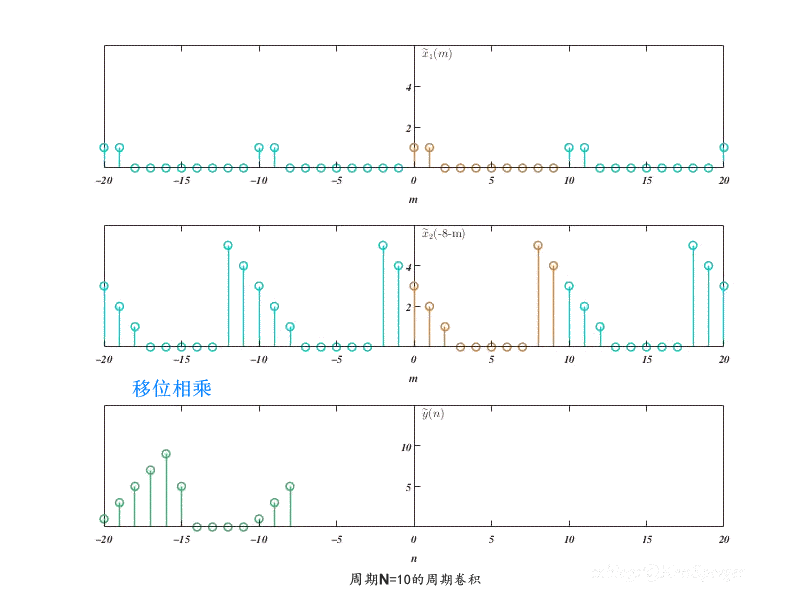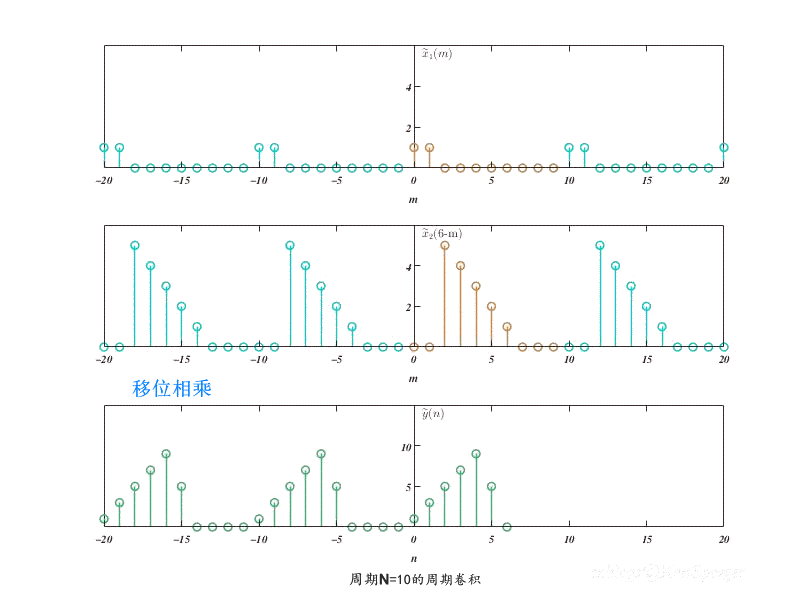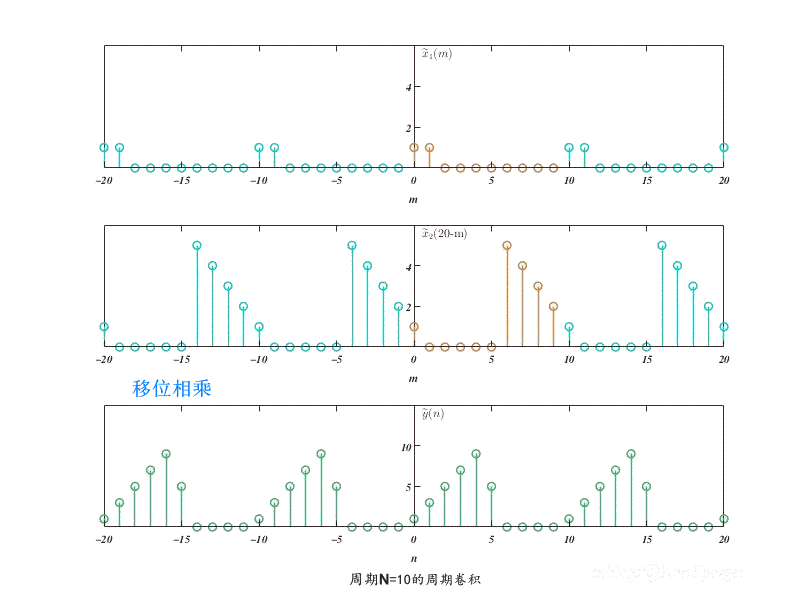
N=5的周期卷积如下,此时$N<N_1+N_2-1$,可以认为序列发生了首位交叠,导致输出与线性卷积结果不同。

圆周卷积
N点的圆周卷积公式为$y(n)=\sum_{m=0}^{\infty} x_1(m) x_2((n-m))_NR_N(n)$。
卷积的过程:先是对两个输入序列进行补0,使得其长度为N;然后在对其中一个序列进行周期延拓,之后跟周期卷积一样进行移位相乘即可。
N=10点的圆周卷积如下。同样$N>N_1+N_2-1$,故卷积结果和线性卷积相同。

N=5点的圆周卷积如下。结果序列首尾各有一点交叠(线性卷积结果的最后一点叠加到了最开始的一点上),其长度为N点。
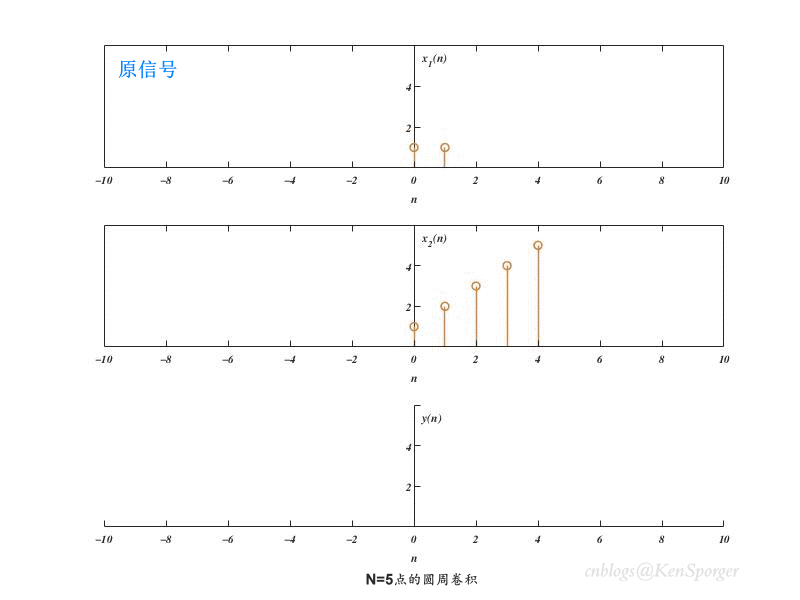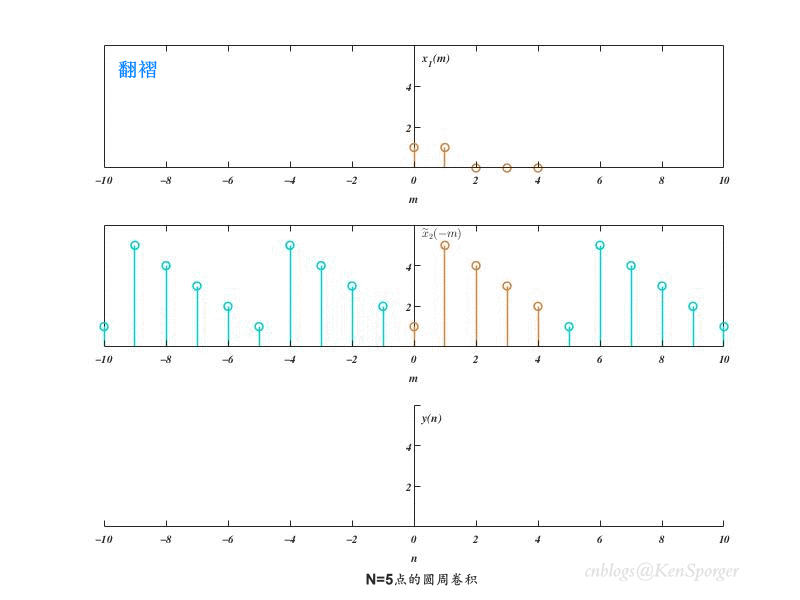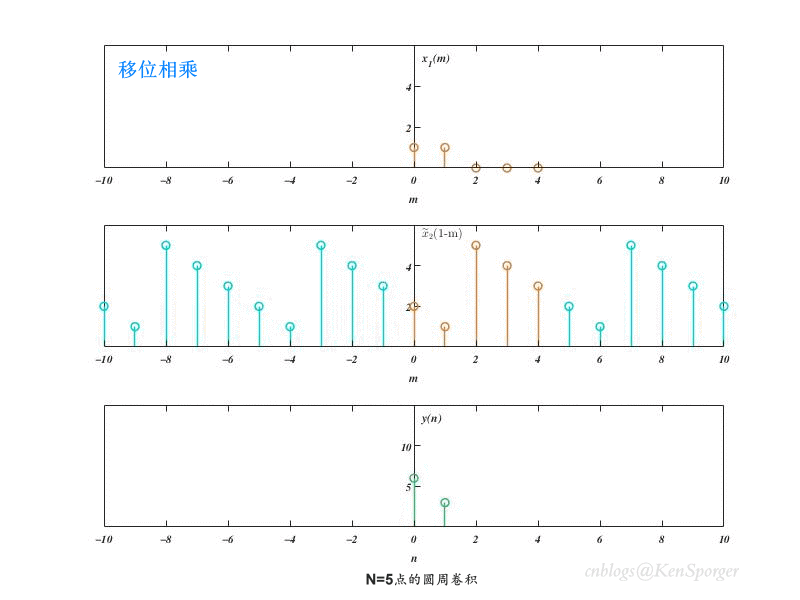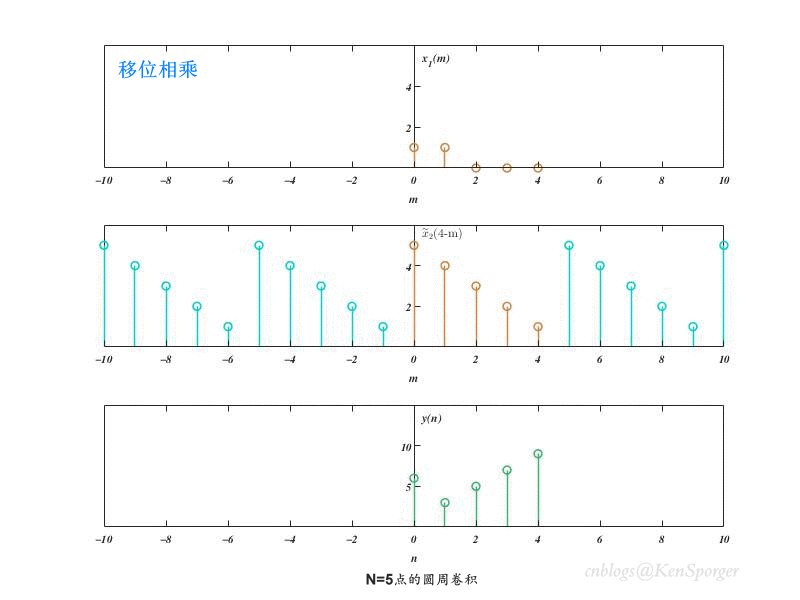
以上结果表明,圆周卷积结果实际上就是周期卷积的主值序列。


