阻抗匹配网络

带载LC电路

　　《PSpice仿真一阶LC谐振电路》一文中对LC空载谐振网络进行了较详细的分析，但在实际应用往往都是带载的情况。以并联LC为例，当网络的输出接上了负载$R_L$，谐振状态下的总电阻将由$R_0$减少为$R_\Sigma = R_0 // R_L$，并且品质因数也不再是$Q_0$，变成$Q_L = \frac{R_\Sigma}{\omega L}$。显然，此时的品质因数显著下降，导致网络的选频能力减弱。

　　为了缓解这个问题，上文曾提出过选择L和C使得$\frac{C}{L}=\frac{1}{rR_L}$来最大化品质因数的方法。此外，我们也希望负载能够尽可能地大，使得并联后的电阻值不会下降得太多，然而这只是我们的一厢情愿。如果负载阻值较小是难以改变的事实，就需要另辟蹊径，从电路本身去着手。阻抗匹配网络就是一个非常好的解决方案。其带来大致三个好处：

　　　　1、改善网络的选频能力。

　　　　2、通过负载和网络输出电阻的匹配、信号源内阻和网络输入电阻的匹配，使信号源功率最大化传输到负载上（并非效率最大化）。

　　　　3、有时负载并非是纯电阻性，会干扰谐振频率点，匹配网络可以使谐振频率更稳定。

 

 

 

匹配网络

　　阻抗匹配网络常见的有三种形式：自耦变压器、互感变压器、电容分压式，前两种都是基于自感和互感原理。这些网络变压的关系基本相似，都定义了一个接入系数$n$，它是小于1的一个数。利用电感匹配的接入系数$n=\frac{N_2}{N_1}$，$N_1、N_2$分别为初级和次级匝数；利用电容分压的接入系数$n= \frac{C_1}{C_1+C_2}$。

 

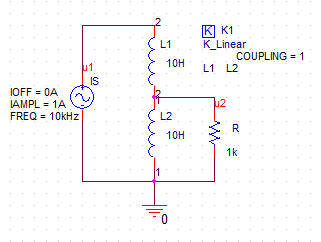
自耦变压器

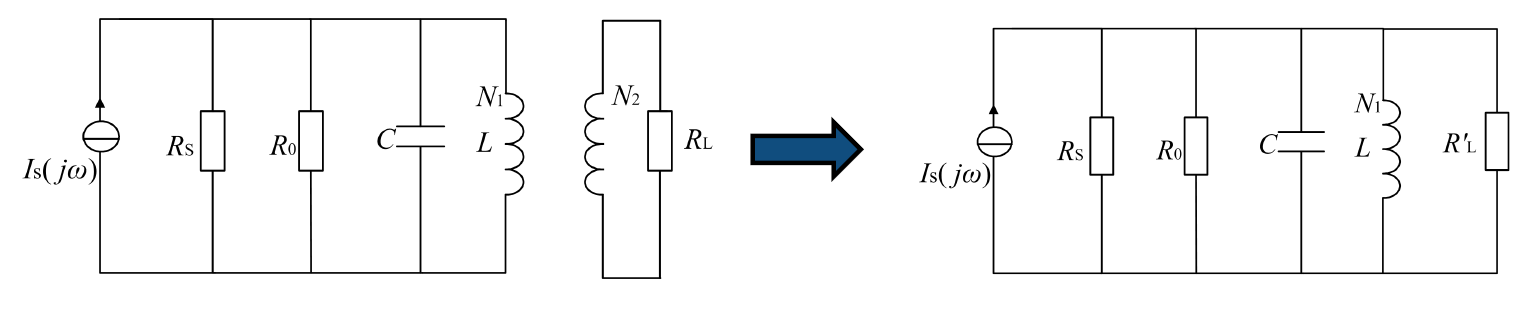
　　如上面的左图所示，自耦变压器采用了电感抽头的方法，即将负载一端搭在电感身上。若$R_L$接入的电感部分匝数为$N_2$，总电感$L$匝数为$N_1$，那么因为是理想的全耦合，则电压之比等于匝数比，即$\frac{U_1^2}{U_2^2}=\frac{N_1^2}{N_2^2}$。

　　对电路进行等效变换得到上面的右图。根据功率相等的原则，$\frac{U_1^2}{R_L'}=\frac{U_2^2}{R_L}$，所以$R_L' = \frac{1}{n^2}R_L$，其中$n=\frac{N_2}{N_1}$。也就是说，通过部分接入，负载阻值相当于被“增大”了。

　　假如负载是一个电容，通过$\frac{U_1^2}{\frac{1}{j\omega C_L'}}=\frac{U_2^2}{\frac{1}{j\omega C_L}}$，可以得到$C_L'=n^2C_L$，那么电路的总电容$C_\Sigma = C_L' + C$显然要比直接把负载电容接在输出端更接近C——谐振频率更稳定。

 

互感变压器

　　互感变压器与自耦变压器原理类似，接入系数$n=\frac{N_2}{N_1}$，$R_L' = \frac{1}{n^2}R_L$，结论一模一样，就不再多说了。

 

电容分压式

　　电容分压式分析的前提条件是$R_L >> \frac{1}{\omega C_2}$，以使得负载接入后流过$C_2$的电流基本没有影响，那么就可以利用电容分压来计算初级和次级电压比：$\frac{U_2}{U_1} = \frac{\frac{1}{j\omega C_2}}{\frac{1}{j\omega C_1} + \frac{1}{j\omega C_2}} = \frac{C_1}{C_1+C2}$。同样再根据功率等效可得$R_L' = \frac{1}{n^2}R_L \; , n=\frac{C_1}{C_1+C2}$。可以看到，等效负载依然相对于真实负载变大了。

 

 

 

 

全耦合变压器

　　变压器实质是电感的耦合，而理想变压器假定电感之间为全耦合，耦合系数K=1。它的变压与线圈数相关，具体表示为$\frac{U_1}{U_2} = \frac{N_1}{N_2}$，其中$U_1、N_1$是初级网络耦合电感的电压和线圈数，$U_2、N_2$是次级网络耦合电感的电压和线圈数，而线圈数和电感值又满足$\frac{N_1}{N_2}=\sqrt { \frac{L_1}{L_2}}$。

 

　　　　　　

 

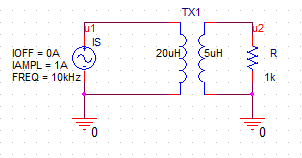
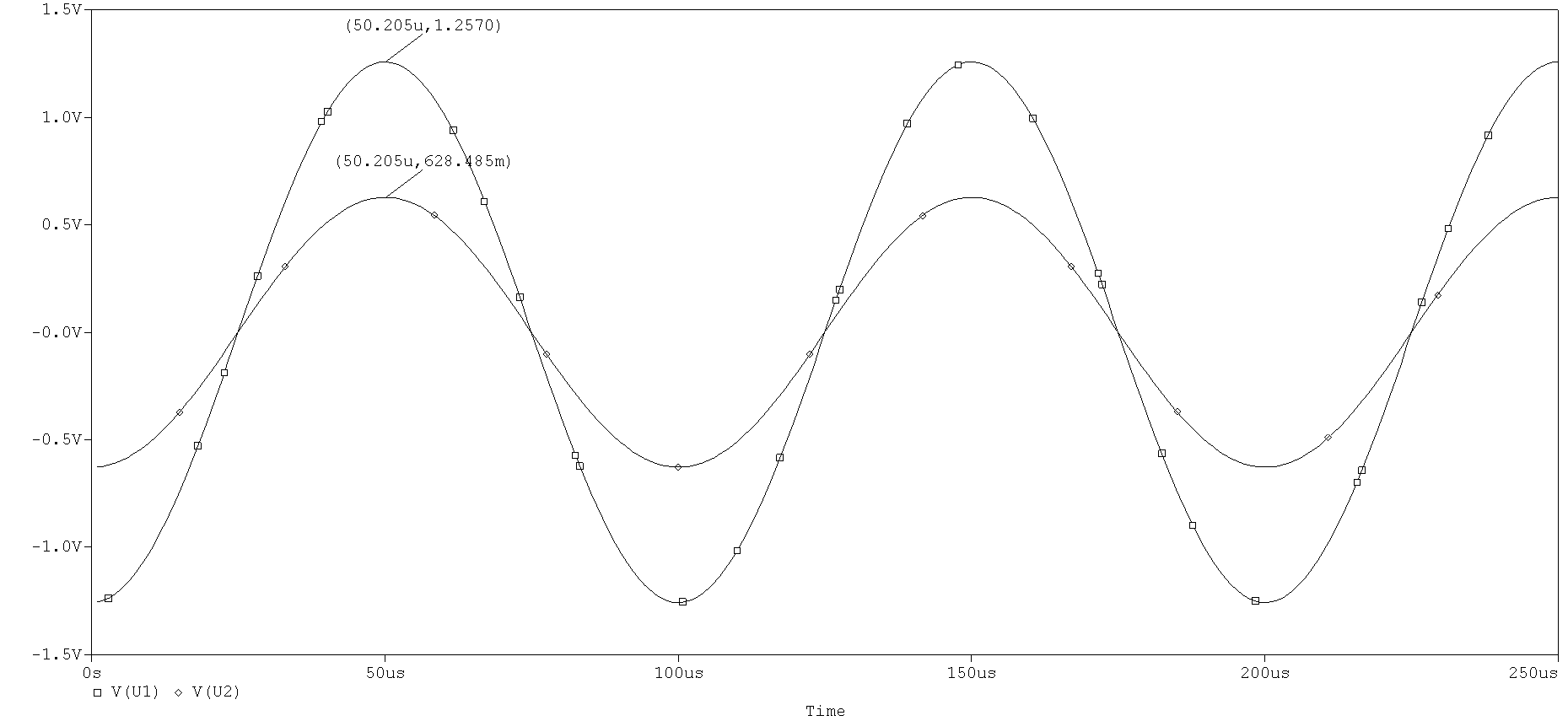
　　上图为全耦合变压器的PSpice仿真电路和电压关系（TX1耦合系数设置为1）。初级的电感是次级电感的四倍，因此匝数比为$\frac{N_1}{N_2}=2$。通过波形结果可以看到，初级电压与次级电压完全同向，幅度是次级的两倍。并且，无论TX1的电感值是多少，只要比值一定，变压倍数就不变。对于初级网络来说，变压器的等效电感就是初级接入的部分，在上图中是$20uH$。

　　电感抽头相对互感要麻烦一点，而且PSpice里也找不到现成的模型，只能引入K_Linear来模拟。如下图所示，其接入系数$n=\frac{\sqrt{L_2}}{\sqrt{L_1}+\sqrt{L_2}}=\frac{1}{2}$，变压关系同上，无论电感取值多少，初级和次级电压都是同向的。对于初级网络来说，等效电感值为$L_1+L_2+2\sqrt{L_1 L_2}$。

 

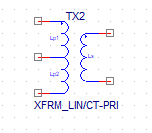
　　PSpice还有另外一种变压器，把上面两种形式组合了起来。由于它涉及到了三个电感的耦合，因此对其的分析比较复杂(本人也没有弄清楚右半部分的接入系数），但左半部分的电感抽头与上面的是一样的结论，等效电感依然是$L_1+L_2+2\sqrt{L_1 L_2}$。

　　

 

 

 

仿真设计

 

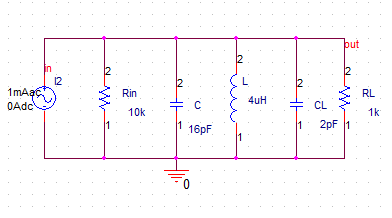
 　　这次仿真对比使用阻抗匹配前后的电路性能，首先是原始的电路图如下。可以计算得到$f_0 \approx 20MHz$、$Q_L = 1.8$、$R_{\Sigma} \approx 0.9K$、$U_m = I_{sm}·R_{\Sigma}=0.9V$、$W(R_L)=0.573mW$，下面右图是仿真结果，可以看到谐振频率发生了偏移，选频能力也并不满意（L和C取值故意取得不好，要不然还不上天）。

　　　　　

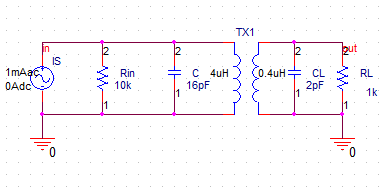
　　接下来使用阻抗匹配对电路进行改善，设计目标是在谐振频率$f_0 \approx 20MHz$的前提下，将电感替换为耦合电感，使得$R_L$和$R_{in}$达到阻抗匹配。我们采用互感变压器形式，根据之前得出的阻抗变换结论，可知接入系数需满足$n^2=\frac{1}{10}$，所以取初级电感值为$4uH$，次级电感值为

 $0.4uH$。电路和仿真结果如下，由图中数据可知，经过阻抗匹配后，初级回路电阻$R_{\Sigma} = 5K$，初级电压$U_{in}=5V$，次级输出电压$U_{out}=nU_{in} \approx 1.58V$。通过计算，$Q_L= 10$，选频能力得到较大提升，负载的功率增大到$2.45mW$。