图像平滑去噪之高斯滤波器
高斯滤波器是根据高斯函数来选择权值的线性平滑滤波器,对随机分布和服从正态分布的噪声有很好地滤除效果。本文从opencv内置的高斯滤波函数入手,深入介绍高斯滤波器的原理与实现。
一、高斯分布函数与高斯卷积核
高斯分布函数指的就是概率论中的正态分布的概率密度函数,均值μ=0时的一维形式和二维形式如下。 其中σ为正态分布的标准偏差,其值决定了函数的衰减快慢。
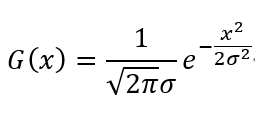

从这两个公式不难看出,二维公式其实等于两个一维函数相乘。从概率论角度看,因为随机变量X,Y是相互独立的,那么他们的联合概率密度就等于边缘概率密度之积。这个特性是非常重要的,后面将再次提及。现在让我们先看一下高斯函数的图像分布与二维高斯卷积核的样子:
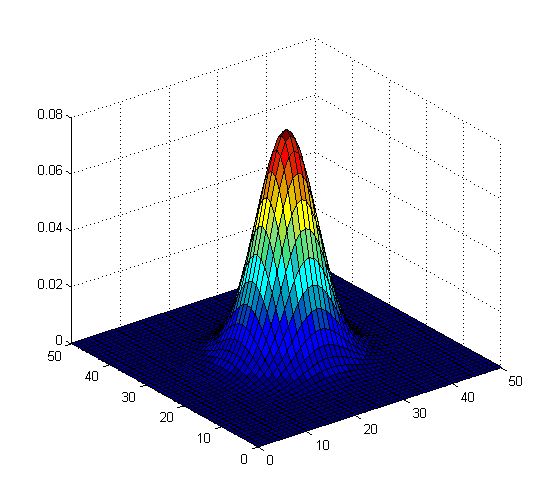
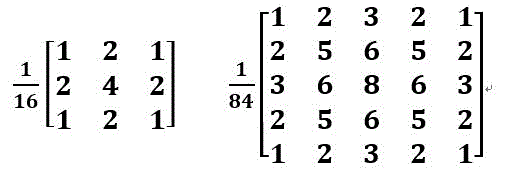
图像上,靠近原点的位置地势高,距离原点越远则地势越低。相应地,卷积核也是中心数值最大,并向四周减小,减小的幅度并不是随意的,而是要求整个卷积核近似高斯函数的图像。由于高斯滤波实质是一种加权平均滤波,为了实现平均,核还带有一个系数,例如上图中的十六分之一、八十四分之一。这些系数等于矩阵中所有数值之和的倒数。
二、高斯滤波
在实际滤波中,将当前像素作为核中心,利用卷积核对周围邻域像素作加权平均,其值作为当前像素的新值。这个过程实质上也是矩阵的卷积(矩阵卷积要求其中一个矩阵要旋转180度,在图像处理时,卷积核可以认为是已经过旋转的矩阵),因此才有卷积核这样的称呼。对于图像边界点,有多种处理方法,如对图像进行扩展、缩小高斯核等。OpenCV中提供了高斯滤波函数:

src为输入的图像,可以是单通道灰度图像,也可以是三通道RGB图像;ksize是卷积核大小,接受tuple类型;sigmaX是水平方向的标准差,sigmaY是垂直方向的标准差,这两个参数可以设置为0,函数内部会根据ksize自动计算标准差,标准差越大,核就越大,核变化趋势就越缓;borderType是边界的处理方式,采取默认值即可。以下是OpenCV-Python的滤波实例:
import cv2 img = cv2.imread('D:/programe/matlab/img/man.jpg') gaussian = cv2.GaussianBlur(img,ksize=(5,5),sigmaX=0,sigmaY=0) cv2.imshow('img',img) cv2.imshow('gaussian',gaussian) cv2.waitKey(0)
滤波前后对比如下图。因为高斯滤波是以空间距离来确定权重大小的,但并没有考虑用颜色距离来确定权重,这样就导致了高斯滤波在去除噪声的同时,也一定程度上模糊了边界。


三、高斯卷积核的构造方法
OpenCV本身就提供了高斯核的生成函数,不过它只能构建一维的核,但是根据上面我们提到过的一维乘积性质,我们可以通过两个一维核向量相乘得到一个二维核,该函数接口和代码如下:

#二维高斯卷积核 def GetGaussianKernel2D(ksize,sigma): kernelX = cv2.getGaussianKernel(ksize[0],sigma).reshape(ksize[0],1)#行向量 kernelY = cv2.getGaussianKernel(ksize[1],sigma).reshape(1,ksize[1])#列向量 kernel = kernelX*kernelY return kernel print(GetGaussianKernel2D((3,3),0.8)) #[[0.05711826 0.12475775 0.05711826] # [0.12475775 0.27249597 0.12475775] # [0.05711826 0.12475775 0.05711826]]
这里sigma是根据经验指定的,实际上更多地是让函数自动计算,标准差的计算公式为:

由于我们需要的是二维核,故可以设置两个标准差,分别表示X方向和Y方向,这两个标准差默认采用公式计算。最终获得的卷积核是小数形式,但是我们像素卷积需要整数,同时为了减小计算开销,我们希望核的值为较小的整数。因此,最常用的做法是将角点化为1,其它点相应乘以相同倍数再四舍五入或者直接去除小数部分,这样使得整个核的值较小,可以加快计算。由于标准差指定可能不同,因此还是会有很多相同大小但值不同的核存在,这并不需要惊讶,因为这些核都符合高斯分布,只是在实际滤波时效果有略微差异罢了。
#二维高斯卷积核 def GetGaussianKernel2D(ksize,sigmaX=None,sigmaY=None): if sigmaX is None: sigmaX = 0.3*((ksize[0]-1)*0.5-1)+0.8 if sigmaY is None: sigmaY = 0.3 * ((ksize[1] - 1) * 0.5 - 1) + 0.8 kernelX = cv2.getGaussianKernel(ksize[0],sigmaX).reshape(ksize[0],1) kernelY = cv2.getGaussianKernel(ksize[1],sigmaY).reshape(1,ksize[1]) kernel = kernelX*kernelY kernel = kernelX*kernelY k = 1/kernel[0,0] kernel = np.int32(kernel*k+0.5) return kernel print(GetGaussianKernel2D((3,3))) #[[1 2 1] # [2 5 2] # [1 2 1]]
四、高斯卷积核的构造原理
我们也可以自己构造核,但首先我们要先知道高斯核与高斯函数之间的关系。以核中心为平面中心,则核的每个元素都对应一个坐标(x,y)如下图所示:
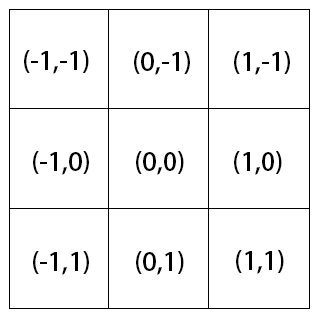
将每个元素对应的坐标代入到二维高斯函数中,得到的函数值作为该位置的值,再经归一化和整数化后就可以得到最终所要的卷积核。
首先构造高斯函数,Python中我没找到可以直接用的接口,所以就自定义算了,注意二维可以不用再写一遍公式,可以通过一维高斯获取:
#一维高斯函数 def Gaussian(x,sigma=1.0): result = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-(x/sigma)**2/2) return result #二维高斯函数 def Gaussian2D(x,y,sigmaX=1.0,sigmaY=1.0): result = Gaussian(x,sigmaX)*Gaussian(y,sigmaY) return result
根据高斯核与高斯函数的关系,定义一维高斯核构造函数:
#一维高斯卷积核 def GaussianKernel(length,sigma=None): radius = length//2 kernel = np.zeros(length,dtype=np.float32) if sigma is None: sigma = 0.3*((length-1)*0.5-1)+0.8 for i in range(length): kernel.itemset(i,Gaussian(i-radius,sigma=sigma)) #归一化 sum = np.sum(kernel) kernel = kernel/sum return kernel
上面的函数就类似于OpenCV的getGaussianKernel。因此二维核也采用相同方法创建即可:
#二维高斯卷积核 def GaussianKernel2D(ksize,sigmaX=None,sigmaY=None): kernelX = GaussianKernel(ksize[0],sigmaX).reshape(ksize[0],1) kernelY = GaussianKernel(ksize[1],sigmaY).reshape(1,ksize[1]) kernel = kernelX*kernelY #整数化 k = 1 / kernel[0, 0] kernel = np.int32(kernel * k + 0.5) return kernel
五、卷积可分离性
在高斯卷积应用中,可能会用到较大的卷积核,此时程序性能就不太令人满意了。卷积可分离性就是解决这种问题的一种优化手段。对于高斯卷积来说,我们可以将图像先与一维水平卷积核相卷积,再与一维垂直方向的卷积核相卷积,所得结果跟直接用二维核来卷积相同,这就是高斯卷积核的可分离性。利用该分离性,卷积复杂度大大降低,并且我们也不需要生成二维卷积核,而只要生成一维核即可,这也减少了计算量。在实际应用中,甚至还可以直接存储常用维数的高斯核数值来提升性能。
下面谈一谈卷积可分离性的原理,不感兴趣的读者可直接阅读下一节。
假设A为n维列向量,B为n维行向量,则有A*B(卷积)=B*A=A·B。例如n=3时,如下图所示:
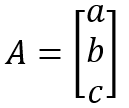
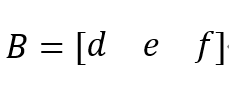

A对B的卷积(A作为核)需要注意先将A向量旋转180度,再做加权求和操作,过程如下:

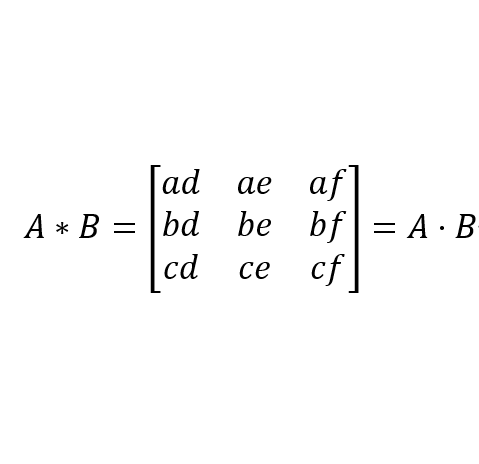
前面说过高斯核Kernel2D=KernelX·KernelY,那么卷积过程就可以表示为:Dst=Src*Kernel2D=(Src*KernelX)*KernelY=(Src*KernelY)*KernelX。一般来说,无论对于何种卷积滤波,只要其卷积核可以拆解为两个行向量与列向量的乘积,那么就算卷积可分离。
六、优化的高斯滤波实现
这一节综合了上面所有代码,并且添加了优化的自定义高斯滤波函数:
import numpy as np import cv2 #一维高斯函数 def Gaussian(x,sigma=1.0): result = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-(x/sigma)**2/2) return result #二维高斯函数 def Gaussian2D(x,y,sigmaX=1.0,sigmaY=1.0): result = Gaussian(x,sigmaX)*Gaussian(y,sigmaY) return result #一维高斯卷积核 def GaussianKernel(length,sigma=None): radius = length//2 kernel = np.zeros(length,dtype=np.float32) if sigma is None: sigma = 0.3*((length-1)*0.5-1)+0.8 for i in range(length): kernel.itemset(i,Gaussian(i-radius,sigma=sigma)) #归一化 sum = np.sum(kernel) kernel = kernel/sum return kernel #二维高斯卷积核 def GaussianKernel2D(ksize,sigmaX=None,sigmaY=None): kernelX = GaussianKernel(ksize[0],sigmaX).reshape(ksize[0],1) kernelY = GaussianKernel(ksize[1],sigmaY).reshape(1,ksize[1]) kernel = kernelX*kernelY k = 1 / kernel[0, 0] kernel = np.int32(kernel * k + 0.5) return kernel #二维高斯卷积核 def GetGaussianKernel2D(ksize,sigmaX=None,sigmaY=None): if sigmaX is None: sigmaX = 0.3*((ksize[0]-1)*0.5-1)+0.8 if sigmaY is None: sigmaY = 0.3 * ((ksize[1] - 1) * 0.5 - 1) + 0.8 kernelX = cv2.getGaussianKernel(ksize[0],sigmaX).reshape(ksize[0],1) kernelY = cv2.getGaussianKernel(ksize[1],sigmaY).reshape(1,ksize[1]) kernel = kernelX*kernelY k = 1/kernel[0,0] kernel = np.int32(kernel*k+0.5) return kernel #优化的高斯滤波 def GaussianFilter(src,ksize): #卷积分离 kernelX = GaussianKernel(ksize[0]) kernelX = np.resize(kernelX,(ksize[0],1)) kernelY = GaussianKernel(ksize[1]) kernelX = np.resize(kernelX, (1,ksize[1])) dst = cv2.filter2D(src,-1,kernelX) dst = cv2.filter2D(dst,-1,kernelY) return dst if __name__ == '__main__': src=cv2.imread('man.jpg') dst = GaussianFilter(src,(5,5)) cv2.imshow('src',src) cv2.imshow('dst',dst) cv2.waitKey(0)

