Java求区间连续最大和的三种解法(含输出起始位置)
先上题
面试华为 OD (社招)的时候给我来了这么一道题,妈耶,没刷过这题,给我虐得,气急败坏,只好跟面试官说不会。但是,谁还愿意服输啊,面试完了,我倒想看看这是个什么类型的题目。
1.1 问题描述
首先,输入一个正整数 N (1<=N<=100000),接着再输入 N 个整数,数值范围为 [-1000,1000]。要求得到子序列的最大和,并求出此时子序列第一个数字的位置,和最后一个数字的位置。
1.2 输入示例
5 6 -1 5 4 -7
1.3 输出示例
14 1 4
分析
力扣类似题型
力扣的题库里有一道类似的题目 连续子数组的最大和,可以去这里面检验一下试试。
给定序列 a[1],a[2],a[3] ... a[n],您的工作是计算子序列的最大和。例如,给定(6,-1, 5, 4,-7),此序列的最大和为 6 +(-1)+ 5 + 4 = 14。
解题
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int arrayLength = in.nextInt();
int[] nums = new int[arrayLength];
for (int i = 0; i < arrayLength; i++) {
nums[i] = in.nextInt();
}
// 通过多态来尝试多种解决方法
Solution maxSum = new ViolentSolution();
// 这里的代码就和力扣原题十分类似了,maxSubArray 的结果稍加改动就可以拿到力扣上去测试了
int[] result = maxSum.maxSubArray(nums);
if (result.length == 3) {
String resultStr = String.format("%d %d %d", result[0], result[1], result[2]);
System.out.println(resultStr);
}
}
public int[] maxSubArray(int[] nums) {
return new int[3];
}
}
Solution 接口
public interface Solution {
/**
* 返回一个包含三个元素的数组,第一个元素表示子序列最大和,第二个元素表示子序列第一个数字的位置,第二个元素表示子序列最后一个数字的位置
*/
int[] maxSubArray(int[] nums);
}
1. 暴力解法
public class ViolentSolution implements Solution {
public int[] maxSubArray(int[] nums) {
int maxSum = nums[0]; // 子序列最大和
int low = 0; // 起始下标
int high = 0; // 结束下标
final int arrayLength = nums.length;
for (int i = 0; i < arrayLength; i++) {
for (int j = i; j < arrayLength; j++) {
int sum = sumOf(nums, i, j);
if (sum > maxSum) {
maxSum = sum;
low = i;
high = j;
}
}
}
// 因为我是从0开始计算的,而返回值要求从1开始
return new int[]{maxSum, low + 1, high + 1};
}
private int sumOf(int[] nums, int i, int j ) {
int sum = 0;
for (int k = i; k <=j ; k++) {
sum += nums[k];
}
return sum;
}
}
思路
划分子序列区间,计算子序列内的值。
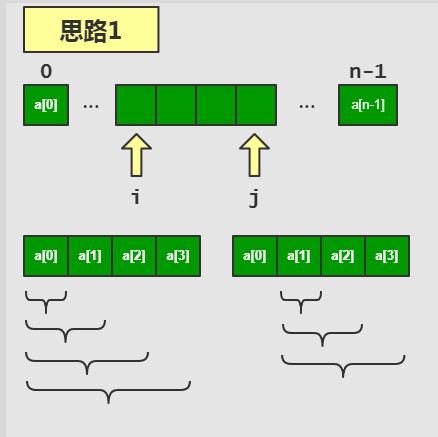
- i, j 可以划分出一个子序列
- i 和 j 从小向大发展
- 依次计算所有子序列的和,并且通过比较,保留下最大的
缺点
时间复杂度高,时间复杂度是 \(O(n^3)\) , 因此 leetcode 也没给通过。

2. 分治法
解题
public class DivideSolution implements Solution {
@Override
public int[] maxSubArray(int[] nums) {
int[] result = maxSubArray(nums, 0, nums.length - 1);
return new int[]{ result[0], result[1] + 1, result[2] + 1};
}
private int[] maxSubArray(int[] nums, int low, int high) {
if (low == high) {
return new int[]{nums[low], low, high};
}
int mid = (low + high) / 2;
int[] leftResult = maxSubArray(nums, low, mid);
int[] rightResult = maxSubArray(nums, mid + 1, high);
int[] midResult = maxSubArray(nums, low, mid, high);
if (leftResult[0] >= rightResult[0] && leftResult[0] >= midResult[0]) {
return leftResult;
} else if (midResult[0] >= leftResult[0] && midResult[0] >= rightResult[0]) {
return midResult;
} else {
return rightResult;
}
}
private int[] maxSubArray(int[] nums, int low, int mid, int high) {
int maxLeftSum = nums[mid];
int leftSum = 0;
int leftIndex = mid;
// 从中点开始往左边增加
for (int i = mid; i >= low; i--) {
leftSum += nums[i];
if (leftSum > maxLeftSum) {
maxLeftSum = leftSum;
leftIndex = i;
}
}
int maxRightSum = nums[mid + 1];
int rightSum = 0;
int rightIndex = mid + 1;
// 从中点开始往右边增加
for (int i = mid + 1; i <= high; i++) {
rightSum += nums[i];
if (rightSum > maxRightSum) {
maxRightSum = rightSum;
rightIndex = i;
}
}
return new int[]{maxLeftSum + maxRightSum, leftIndex, rightIndex};
}
}
3.动态规划
动态规划解析(摘自力扣精选答案):
状态定义: 设动态规划列表 \(dp\) ,\(dp[i]\) 代表以元素 \(nums[i]\) 为结尾的连续子数组最大和。
- 为何定义最大和 \(dp[i]\) 中必须包含元素 \(nums[i]\) :保证 \(dp[i]\) 递推到 \(dp[i+1]\) 的正确性;如果不包含 \(nums[i]\) ,递推时则不满足题目的 连续子数组 要求。
转移方程: 若 \(dp[i-1] ≤ 0\),说明 \(dp[i−1]\) 对 \(dp[i]\) 产生负贡献,即 \(dp[i-1] + nums[i]\) 还不如 \(nums[i]\) 本身大。
当 \(dp[i - 1] > 0\) 时:执行 \(dp[i] = dp[i-1] + nums[i]\);
当 \(dp[i - 1] ≤ 0\) 时:执行 \(dp[i] = nums[i]\) ;
初始状态: \(dp[0] = nums[0]\),即以 \(nums[0]\) 结尾的连续子数组最大和为 nums[0] 。
返回值: 返回 \(dp\) 列表中的最大值,代表全局最大值。

解题
public class DynamicSolution implements Solution {
@Override
public int[] maxSubArray(int[] nums) {
// 准备一个数组来缓存结果
// dp[i] 存储 nums[0...i] 子序列的最大和且必须包含 nums[i]
int[] dp = new int[nums.length];
// 存储子序列的起始位置
int[] start = new int[nums.length];
// 赋予初始值
dp[0] = nums[0];
start[0] = 0;
for (int i = 1; i < dp.length; i++) {
// 递推公式
if (dp[i - 1] < 0) { // 负贡献,不参与累加
dp[i] = nums[i];
start[i] = i; // 起始位置重置
} else {
dp[i] = nums[i] + dp[i - 1];
start[i] = start[i - 1]; // 延续起始位置
}
}
int maxSum = dp[0];
int low = 0;
int high = 0;
for (int i = 1; i < dp.length; i++) {
if (dp[i] > maxSum) {
maxSum = dp[i];
low = start[i];
high = i;
}
}
return new int[]{maxSum, low + 1, high + 1};
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号