Sparse AutoEncoder简介

1. AutoEncoder

  AutoEncoder是一种特殊的三层神经网络, 其输出等于输入:\(y^{(i)}=x^{(i)}\), 如下图所示:

        

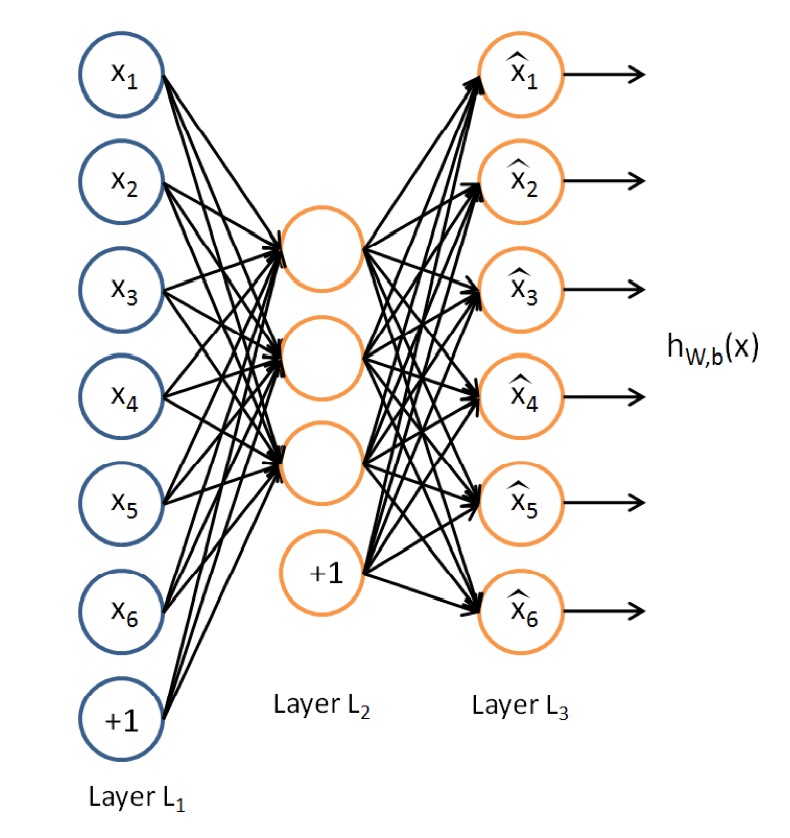
  亦即AutoEncoder想学到的函数为\(f_{W,b} \approx x\), 来使得输出\(\hat{x}\)比较接近x. 乍看上去学到的这种函数很平凡, 没啥用处, 实际上, 如果我们限制一下AutoEncoder的隐藏单元的个数小于输入特征的个数, 便可以学到数据的很多有趣的结构. 如果特征之间存在一定的相关性, 则AutoEncoder会发现这些相关性.

  2. Sparse AutoEncoder

  我们可以限制隐藏单元的个数来学到有用的特征, 或者可以对网络施加其他的限制条件, 而不限制隐藏单元的个数. 特别的, 我们可以对隐藏单元施加稀疏性限制. 具体的, 一个神经元是激活的当且仅当其输出值比较接近1, 一个神经元是不激活的当且仅当其输出值比较接近0. 我们可以限制神经元在大多数时间下都是不激活的(亦即Sparse Filtering中的Lifetime Sparsity概念).

  定义\(a_j^{(2)}\)为AutoEncoder中隐藏单元的激活值, 我们形式化的定义如下的限制:$${\hat{\rho}}_j=\frac{1}{m}\sum_{i=1}^{m}[a_j^{2}(x^{(i)})]=\rho$$

  其中\(\rho\)是稀疏性参数, 一般取值为一个比较接近0的数, 比如0.05. 

  为了使得学到的AutoEncoder达到上述的稀疏性要求, 我们在优化目标里添加了新的一项, 用于惩罚那些偏离\(\rho\)太多的\(\hat{\rho}_j\). 可以使用KL Divergence:$$\sum_{j=1}^{s_2} \rho log \frac{\rho}{\hat{\rho}_j}+(1-\rho)log\frac{1-\rho}{1-\hat{\rho}_j}$$

  上式可也以写作:$$\sum_{j=1}^{s_2}KL(\rho||\hat{\rho}_j)$$

  下图展示了KL Divergence的特性: \(\hat{\rho}_j\)越接近\(\rho\)(此处为0.2), 则KL Divergence越小.

  

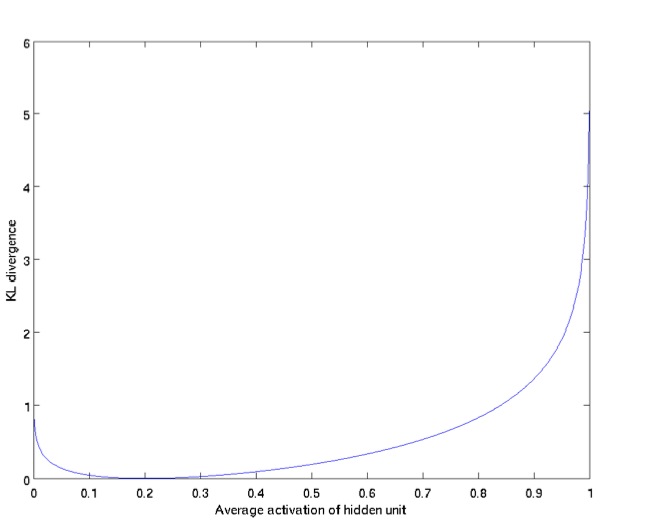
  所以, Sparse AutoEncoder的损失函数为:$$\mathit{J}_{sparse}(\mathit{W},\mathit{b})=\mathit{J}(\mathit{W},\mathit{b}) + \beta\sum_{j=1}^{s_2}KL(\rho||\hat{\rho}_j)$$

  其中$$\mathit{J}(\mathit{W},\mathit{b})=\left[\frac{1}{m}\sum_{i=1}^{m}\mathit{J}(\mathit{W},\mathit{b};\mathit{x}^{(i)},\mathit{j}^{(i)})\right]+\frac{\lambda}{2}\sum_{l=1}^{n_l-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}\left(\mathit{W}_{ji}^{(l)}\right) ^2=\left[\frac{1}{m}\sum_{i=1}^{m}\left(\frac{1}{2}\left|\left|h_{\mathit{W,b}}(x^{(i)})-y^{(i)}\right|\right| ^2\right)\right]+\frac{\lambda}{2}\sum_{l=1}^{n_l-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}\left(\mathit{W}_{ji}^{(l)}\right) ^2$$

  添加KL Divergence后的cost function后的偏导数为:

     

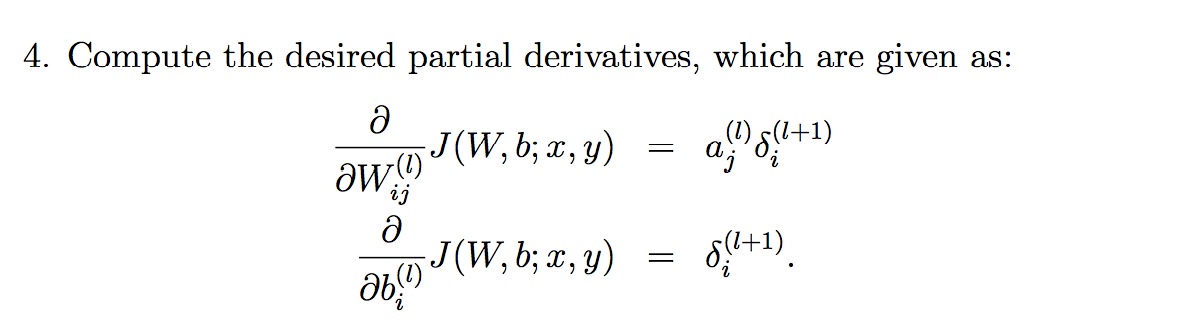
  有个新的偏导数之后, 使用Back Propagation来优化整个神经网络:

  参考文献:

  [1]. Sparse AutoEncoder. Andrew Ng.