[算法经典] 约瑟夫环问题
原文链接:https://blog.csdn.net/u011500062/article/details/72855826
约瑟夫问题
约瑟夫问题是个著名的问题:N个人围成一圈,第一个人从1开始报数,报M的将被杀掉,下一个人接着从1开始报。如此反复,最后剩下一个,求最后的胜利者。
例如只有三个人,把他们叫做A、B、C,他们围成一圈,从A开始报数,假设报2的人被杀掉。
●首先A开始报数,他报1。侥幸逃过一劫。
●然后轮到B报数,他报2。非常惨,他被杀了
●C接着从1开始报数
●接着轮到A报数,他报2。也被杀死了。
●最终胜利者是C
解决方案
普通解法
刚学数据结构的时候,我们可能用链表的方法去模拟这个过程,N个人看作是N个链表节点,节点1指向节点2,节点2指向节点3,……,节点N-1指向节点N,节点N指向节点1,这样就形成了一个环。然后从节点1开始1、2、3……往下报数,每报到M,就把那个节点从环上删除。下一个节点接着从1开始报数。最终链表仅剩一个节点。它就是最终的胜利者。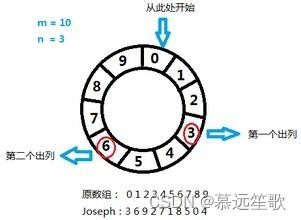
缺点:
要模拟整个游戏过程,时间复杂度高达O(nm),当n,m非常大(例如上百万,上千万)的时候,几乎是没有办法在短时间内出结果的。
公式法
约瑟夫环是一个经典的数学问题,我们不难发现这样的依次报数,似乎有规律可循。为了方便导出递推式,我们重新定义一下题目。
问题: N个人编号为1,2,……,N,依次报数,每报到M时,杀掉那个人,求最后胜利者的编号。
这边我们先把结论抛出了。之后带领大家一步一步的理解这个公式是什么来的。
递推公式:
f(N,M)=(f(N−1,M)+M)%N
- 1
●f(N,M)表示,N个人报数,每报到M时杀掉那个人,最终胜利者的编号
●f(N−1,M)表示,N-1个人报数,每报到M时杀掉那个人,最终胜利者的编号
下面我们不用字母表示每一个人,而用数字。
1、2、3、4、5、6、7、8、9、10、11
表示11个人,他们先排成一排,假设每报到3的人被杀掉。
●刚开始时,头一个人编号是1,从他开始报数,第一轮被杀掉的是编号3的人。
●编号4的人从1开始重新报数,这时候我们可以认为编号4这个人是队伍的头。第二轮被杀掉的是编号6的人。
●编号7的人开始重新报数,这时候我们可以认为编号7这个人是队伍的头。第三轮被杀掉的是编号9的人。
●……
●第九轮时,编号2的人开始重新报数,这时候我们可以认为编号2这个人是队伍的头。这轮被杀掉的是编号8的人。
●下一个人还是编号为2的人,他从1开始报数,不幸的是他在这轮被杀掉了。
●最后的胜利者是编号为7的人。
下图表示这一过程(先忽视绿色的一行)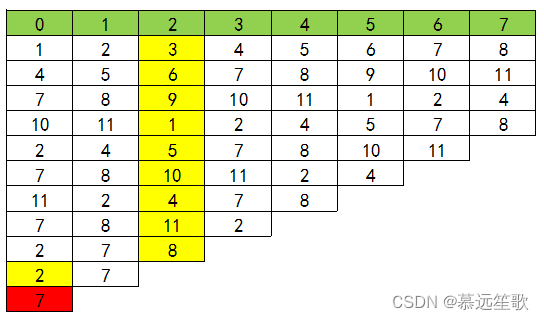
现在再来看我们递推公式是怎么得到的!
将上面表格的每一行看成数组,这个公式描述的是:幸存者在这一轮的下标位置
●f(1,3):只有1个人了,那个人就是获胜者,他的下标位置是0
●f ( 2 , 3 ) = ( f ( 1 , 3 ) + 3 ) % 2 = 3 % 2 = 1 f(2,3)=(f(1,3)+3)%2=3%2=1f(2,3)=(f(1,3)+3)%2=3%2=1:在有2个人的时候,胜利者的下标位置为1
●f ( 3 , 3 ) = ( f ( 2 , 3 ) + 3 ) % 3 = 4 % 3 = 1 f(3,3)=(f(2,3)+3)%3=4%3=1f(3,3)=(f(2,3)+3)%3=4%3=1:在有3个人的时候,胜利者的下标位置为1
●f ( 4 , 3 ) = ( f ( 3 , 3 ) + 3 ) % 4 = 4 % 4 = 0 f(4,3)=(f(3,3)+3)%4=4%4=0f(4,3)=(f(3,3)+3)%4=4%4=0:在有4个人的时候,胜利者的下标位置为0
●……
f● ( 11 , 3 ) = 6 f(11,3)=6f(11,3)=6
很神奇吧!现在你还怀疑这个公式的正确性吗?上面这个例子验证了这个递推公式的确可以计算出胜利者的下标,下面将讲解怎么推导这个公式。
问题1: 假设我们已经知道11个人时,胜利者的下标位置为6。那下一轮10个人时,胜利者的下标位置为多少?
答: 其实吧,第一轮删掉编号为3的人后,之后的人都往前面移动了3位,胜利这也往前移动了3位,所以他的下标位置由6变成3。
问题2: 假设我们已经知道10个人时,胜利者的下标位置为3。那下一轮11个人时,胜利者的下标位置为多少?
答: 这可以看错是上一个问题的逆过程,大家都往后移动3位,所以f ( 11 , 3 ) = f ( 10 , 3 ) + 3 f(11,3)=f(10,3)+3f(11,3)=f(10,3)+3。不过有可能数组会越界,所以最后模上当前人数的个数,f ( 11 , 3 ) = ( f ( 10 , 3 ) + 3 ) % 11 f(11,3)=(f(10,3)+3)%11f(11,3)=(f(10,3)+3)%11
问题3: 现在改为人数改为N,报到M时,把那个人杀掉,那么数组是怎么移动的?
答: 每杀掉一个人,下一个人成为头,相当于把数组向前移动M位。若已知N-1个人时,胜利者的下标位置位f ( N − 1 , M ) f(N-1,M)f(N−1,M),则N个人的时候,就是往后移动M为,(因为有可能数组越界,超过的部分会被接到头上,所以还要模N),既f ( N , M ) = ( f ( N − 1 , M ) + M ) % n f(N,M)=(f(N-1,M)+M)%nf(N,M)=(f(N−1,M)+M)%n
注:理解这个递推式的核心在于关注胜利者的下标位置是怎么变的。每杀掉一个人,其实就是把这个数组向前移动了M位。然后逆过来,就可以得到这个递推式。
因为求出的结果是数组中的下标,最终的编号还要加1
下面给出代码实现:
class Solution {
public int findTheWinner(int n, int k) {
int p = 0;
for (int i = 2; i <= n; i++) {
p = (p + k) % i;
}
return p + 1;
}
} 版权声明:本文为CSDN博主「陈浅墨」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
——————————————————————————————————————————————————————————————————————————
原文链接:https://blog.csdn.net/qq_40692274/article/details/124592025
【前言】本文讨论经典算法问题约瑟夫环问题的递归解法。
一、问题描述
作为算法中的经典问题,约瑟夫环问题自诞生以来有各种各样的变种描述,丢手绢、游戏获胜者、圆圈中最后剩下的数字、点名游戏等等,但都是同样的数学模型和解题思路。为了讨论该问题,现在将其统一描述如下:
0 , 1 , … , n-1 这 n 个数字围成一个圆,从数字 0 开始,每次从这个圆里删除第 m 个数字(删除后从下一个数字开始重新计数)。求这个圆圈里剩下的最后一个数字是多少。
样例
输入:int n = 6, int m = 3
输出:int ret = 0
讲解:
0, 1, 2, 3, 4, 5 从0开始删除第3个数字,012,2退出
0, 1, 3, 4, 5 从3开始删除第3个数字,345,5退出
0, 1, 3, 4 从0开始删除第3个数字,013,3退出
0, 1, 4 从4开始删除第3个数字,401,1退出
0, 4 从4开始删除第3个数字,404,4退出
0是最后剩下的数字
二、递归解法
本文不再讲解 数组模拟 的解法,直接讨论递归法。约定用记号f(n,m)表示n个数、每次删除第m个时该问题的解,例如由上述样例就有f(6,3)=0。
1、思路分析
我们再来仔细推演f(6,3)的计算过程,“ 0, 1, 2, 3, 4, 5 ”在第一轮中有6个数字,删除从0开始的第3个数字“ 2 ”以后剩下“ 0, 1, 3, 4, 5 ”。接着的第二轮中还有5个数字,要从“ 3 ”开始继续删除第3个数字,由于这些数字围成一个圆,我们不妨把“ 0, 1 ”放在“ 3, 4, 5 ”的后面变成“ 3, 4, 5, 0, 1 ”方便计算。
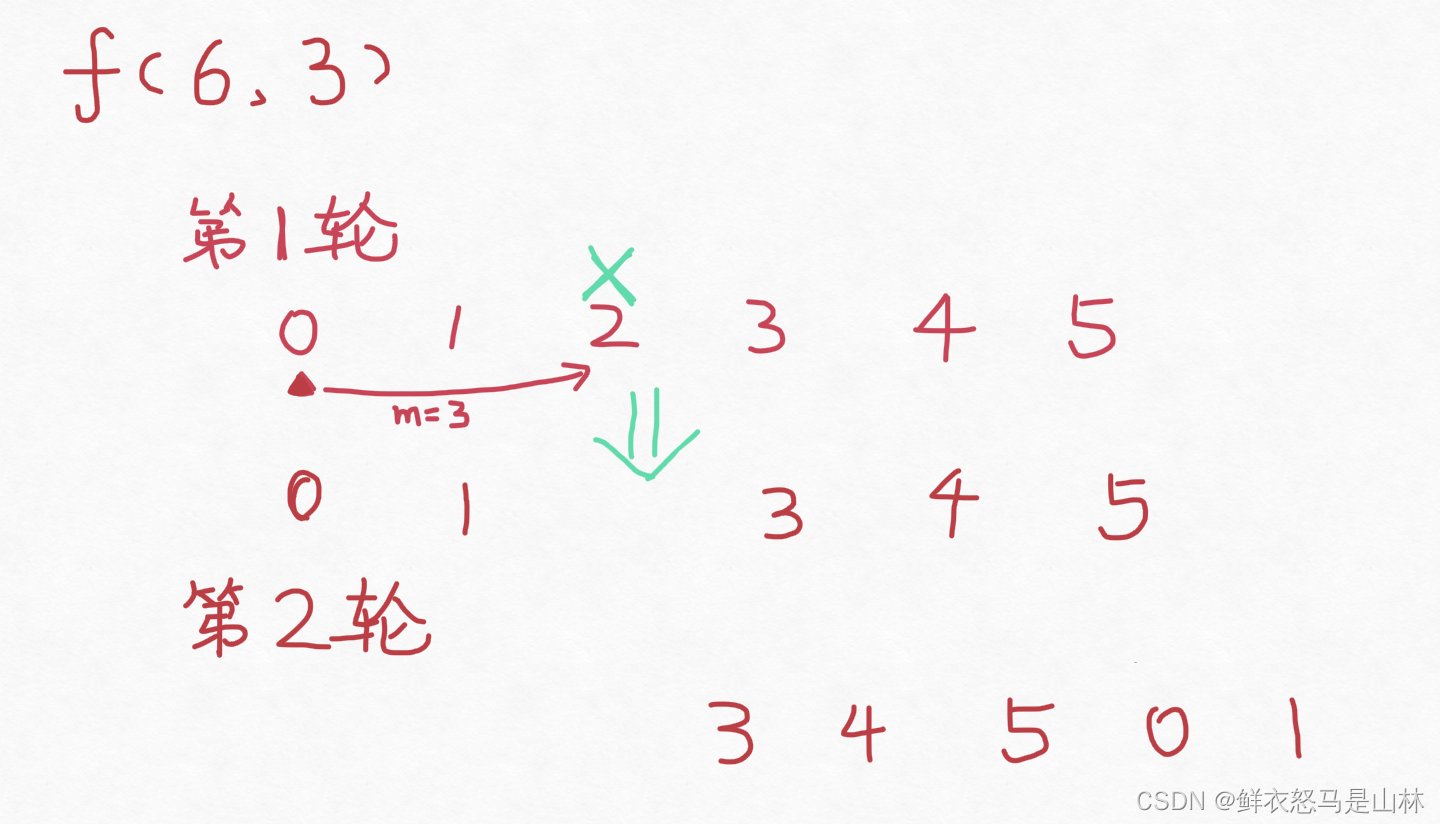
调整位置后,第2轮的f(6,3)不禁我们联想到f(5,3),f(5,3)第1轮和f(6,3)第2轮同样有5个数字、同样从第1个位置开始删除第3个数字,换言之,他们要删除的元素位置是一样的,不一样的仅仅是位置上的值。只要我们能找到相同位置上值的关系,就能通过f(5,3)求出f(6,3)、f(4,3)求出f(5,3)、f(3,3)求出f(4,3),直到利用f(1,3)=0回溯。
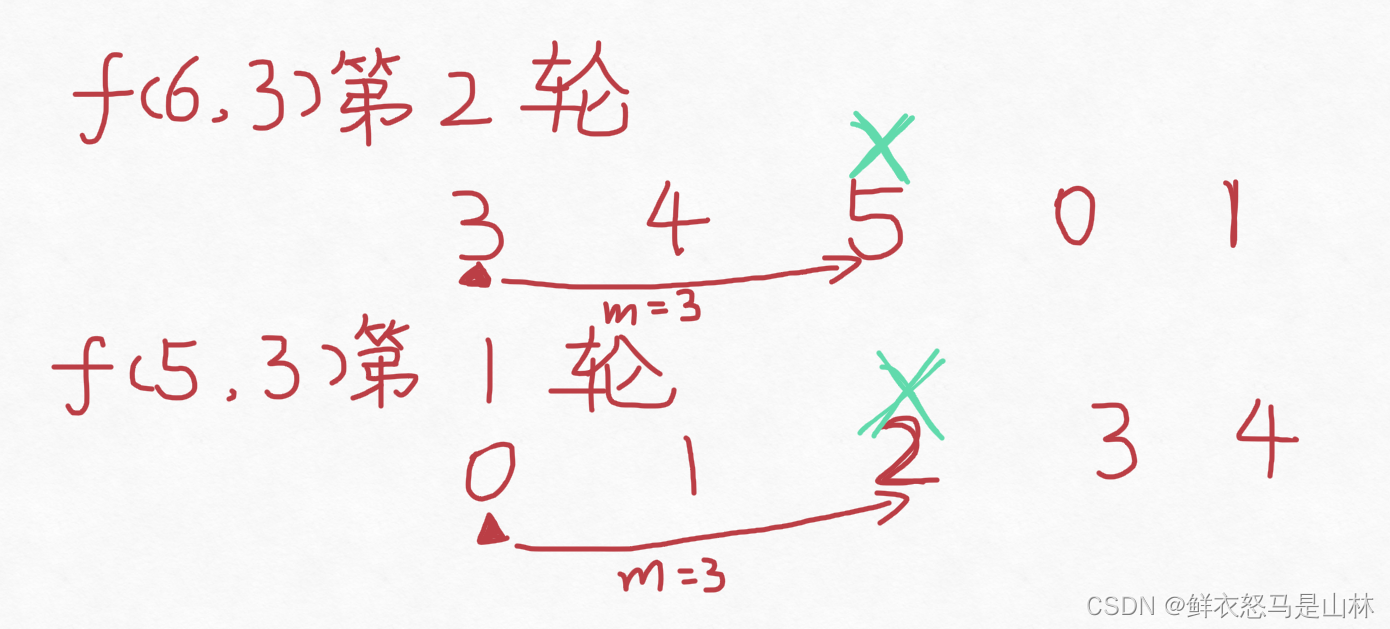
观察后发现,f(5,3)中的0对应f(6,3)的3、1对应4、2对应5、3对应0、4对应1,也即f(6,3) = ( f(5,3)+3 ) % 6。如果继续列举就会进一步发现:f(5,3) = ( f(4,3)+3 ) % 6、f(4,3) = ( f(3,3)+3 ) % 6…由此我们就找到了f(n,m)的通项公式为
f(n,m) = ( f(n-1,m)+m ) % n 直到f(1,m)=0
利用这个公式,我们可以很容易地使用递归法解决约瑟夫环问题。
2、源代码
private int lastNum(int n, int m)
{
if (n==1)
return 0;
return ( lastNum(n-1,m)+m ) % n;
}
3、复杂度分析
时间复杂度:O(n) 对n个数要计算n次f(n,m)
空间复杂度:O(n) 计算n次f(n,m)时递归n-1次
————————————————



 浙公网安备 33010602011771号
浙公网安备 33010602011771号