透彻理解迪杰斯特拉算法
透彻理解迪杰斯特拉算法
转自：http://blog.csdn.net/mu399/article/details/50903876
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，这个算法我主动学了三遍，第一主动学的时候，是看严蔚敏的《数据结构》，当时应该是学懂了，有点透彻地理解了这个算法，但是没有记录下来，后来就忘记了， 第二次主动学，就去网上找相关文章，看了不少关于这个算法的讲解，但总感觉都没有讲透，看得我二懂二懂的，昨天晚上，突然又想到这个算法，发现我还是不熟悉这个算法，又忘记Dijkstra 算法是怎么一回事了，决定再看这个算法一遍，虽然已经快12点了，平时这个时候已经躺床上了。 这次终于彻底搞懂，并决定写成博客记录下来。
Dijkstra 算法，用于对有权图进行搜索，找出图中两点的最短距离，既不是DFS搜索，也不是BFS搜索。
把Dijkstra 算法应用于无权图，或者所有边的权都相等的图，Dijkstra 算法等同于BFS搜索。
http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
2.算法描述
1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
执行动画过程如下图
例子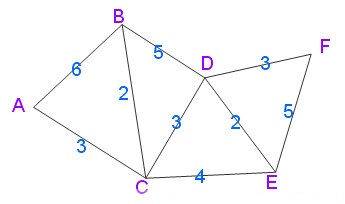 
不要看算法的动画，理解算法的时候，思维更不上GIF动画的速度，这两张图对理解算法最管用
重点需要理解这句拗口的”按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度”
实际上，Dijkstra 算法是一个排序过程，就上面的例子来说，是根据A到图中其余点的最短路径长度进行排序，路径越短越先被找到，路径越长越靠后才能被找到，要找A到F的最短路径，我们依次找到了
A –> C 的最短路径 3
A –> C –> B 的最短路径 5
A –> C –> D 的最短路径 6
A –> C –> E 的最短路径 7
A –> C –> D –> F 的最短路径 9
Dijkstra 算法运行的附加效果是得到了另一个信息，A到C的路径最短，其次是A到B, A到D, A到E, A到F
为什么Dijkstra 算法不适用于带负权的图？
就上个例子来说，当把一个点选入集合S时，就意味着已经找到了从A到这个点的最短路径，比如第二步，把C点选入集合S，这时已经找到A到C的最短路径了，但是如果图中存在负权边，就不能再这样说了。举个例子，假设有一个点Z，Z只与A和C有连接，从A到Z的权为50，从Z到C的权为-49，现在A到C的最短路径显然是A –> Z –> C
对带负权的图，应该用Floyd算法
