什么是神经网络?用代码示例解析其工作原理
神经网络是一种模仿人脑神经元工作原理的计算模型,用于实现机器学习和人工智能系统。它由一系列相互连接的神经元(也称为节点或单元)组成,这些神经元组织成不同的层。神经网络通常包括输入层、一个或多个隐藏层和输出层。每个节点根据其输入数据和相应的权重计算输出值,并通过激活函数进行非线性转换。
神经网络可以通过学习和调整权重实现自适应,从而在处理复杂问题(如图像识别、自然语言处理和游戏策略等)时具有很高的灵活性。训练神经网络的过程通常包括使用大量输入数据和期望输出,计算损失函数(用于衡量网络输出与期望输出之间的差距),并使用优化算法(如梯度下降法)调整权重以最小化损失。
神经网络是深度学习的核心组成部分,深度学习模型通常包含多个隐藏层,从而能够学习更复杂数学表示和抽象概念。
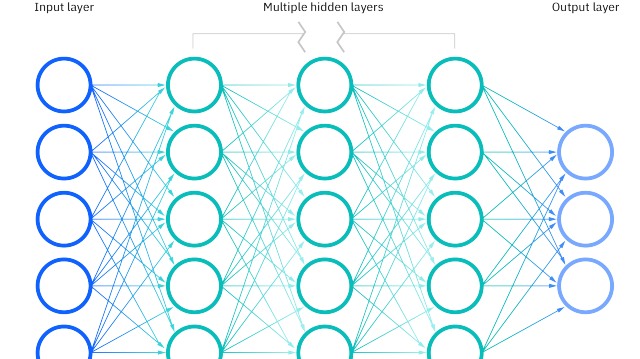
下面以一个简单的神经网络(用于解决 XOR 问题)为例,说明神经网络中的各个概念。
该神经网络示例中,包含一个输入层(2个节点),一个隐藏层(2个节点)和一个输出层(1个节点)。输入输出层之间以及隐藏层与输出层之间的所有节点均相互连接。激活函数为 Sigmoid 函数。
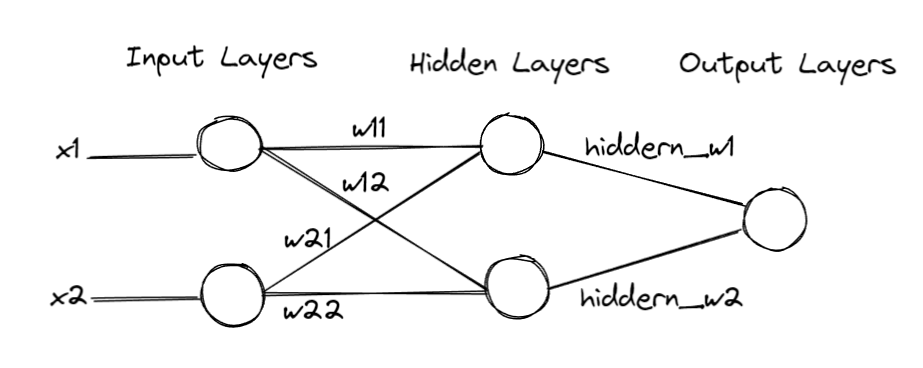
上述神经网络的python实现如下:
import numpy as np # Sigmoid 激活函数 def sigmoid(x): return 1 / (1 + np.exp(-x)) # 使用 sigmoid 导数进行非线性变换以及反向传播计算梯度 def sigmoid_derivative(x): return x * (1 - x) def mse_loss(y_true, y_pred): return np.mean(np.square(y_true - y_pred)) class NeuralNetwork: def __init__(self, input_nodes, hidden_nodes, output_nodes): self.input_nodes = input_nodes self.hidden_nodes = hidden_nodes self.output_nodes = output_nodes self.weights_ih = np.random.rand(self.input_nodes, self.hidden_nodes) - 0.5 self.weights_ho = np.random.rand(self.hidden_nodes, self.output_nodes) - 0.5 self.bias_h = np.random.rand(1, self.hidden_nodes) - 0.5 self.bias_o = np.random.rand(1, self.output_nodes) - 0.5 def feedforward(self, input_data): hidden = sigmoid(np.dot(input_data, self.weights_ih) + self.bias_h) output = sigmoid(np.dot(hidden, self.weights_ho) + self.bias_o) return hidden, output def backward(self, input_data, hidden, output, target_data, learning_rate=0.1): # 计算损失函数的梯度 output_error = target_data - output output_delta = output_error * sigmoid_derivative(output) hidden_error = np.dot(output_delta, self.weights_ho.T) hidden_delta = hidden_error * sigmoid_derivative(hidden) self.weights_ho += learning_rate * np.dot(hidden.T, output_delta) self.weights_ih += learning_rate * np.dot(input_data.T, hidden_delta) self.bias_o += learning_rate * np.sum(output_delta, axis=0) self.bias_h += learning_rate * np.sum(hidden_delta, axis=0) # 根据输入输出数据,训练多轮,更新神经网络的权重和偏置,最终得到正确的神经网络参数 def train(self, input_data, target_data, epochs, learning_rate=0.5): for _ in range(epochs): hidden, output = self.feedforward(input_data) self.backward(input_data, hidden, output, target_data, learning_rate) if __name__ == "__main__": # 示例 X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) Y = np.array([[0], [1], [1], [0]]) nn = NeuralNetwork(input_nodes=2, hidden_nodes=2, output_nodes=1) print("Before training:") _, output = nn.feedforward(X) print(output) nn.train(X, Y, epochs=2000, learning_rate=0.8) print("After training:") _, output = nn.feedforward(X) print(output) # 计算损失 loss = mse_loss(Y, output) print("Loss:", loss)
-
首先,创建 XOR 问题的输入和输出数据集,分别存储在 NumPy 数组中
-
初始化权重与偏置
-
然后,根据输入输出数据,训练2000轮
-
每轮训练都会通过反向传播更新各层的权重和偏置,最终得到正确的神经网络参数
上述简单示例中,涉及到如下神经网络基本概念:
-
前向传播:利用若干个权重系数矩阵W,偏倚向量b来和输入值向量x进行一系列线性运算和激活运算,从输入层开始,一层层的向后计算,一直到运算到输出层,得到输出结果为值
-
激活函数:(Activation Function)是一种在神经网络中使用的非线性函数,用于将神经元的累积输入值转换为输出值。激活函数的主要目的是引入非线性特性,使得神经网络能够学习并表示复杂的数据模式。如果没有激活函数,神经网络将仅仅是一个线性回归模型,无法处理复杂的问题。
-
反向传播:核心思想是通过优化权重与偏置,从而逐渐减小预测输出与真实值之间的差距,提高神经网络的性能。反向传播过程开始于计算输出层的误差,即预测输出与实际目标之间的差值。然后,这个误差将从输出层向后传播到隐藏层。为了更新神经网络中的权重,我们需要计算损失函数相对于每个权重的梯度。我们使用链式法则(chain rule)将这些梯度分解为前一层的输出、当前层的梯度和后一层的梯度。通过这种方式,我们可以得到每个权重的梯度,并用它们更新权重以最小化损失。
-
损失函数:损失函数值在训练过程中起到的作用是衡量模型预测结果与实际目标值之间的差距。在反向传播过程中,我们实际上是通过损失函数的梯度来调整神经网络的权重和偏置,从而使得损失值最小化。
在上面的代码示例中,我们计算了输出层的误差(output_error),这个误差实际上就是损失函数的梯度。这里的损失函数是均方误差(MSE),计算梯度的公式为:
output_error = target_data - output
在反向传播过程中,我们通过该梯度来更新权重和偏置,以使得损失值最小化。因此,损失值在训练过程中起到了关键作用。
其中,Sigmoid 函数是一种常用的激活函数,用于神经网络中对节点输出进行非线性转换。Sigmoid 函数的数学表达式如下:
sigmoid(x) = 1 / (1 + e^(-x))
其中,x 是输入值,e 是自然常数(约等于 2.71828)。
Sigmoid 函数的输出值范围在 0 和 1 之间,具有平滑的 S 形曲线。当输入值 x 趋向于正无穷大时,函数值接近 1;当输入值 x 趋向于负无穷大时,函数值接近 0。因此,Sigmoid 函数可以将任意实数输入映射到 (0, 1) 区间内,使得网络输出具有更好的解释性。此外,Sigmoid 函数的导数也可以方便地用其函数值表示,便于进行梯度下降优化算法。
然而,Sigmoid 函数也存在一些问题,例如梯度消失问题。当输入值过大或过小时,Sigmoid 函数的梯度(导数)接近于 0,导致权重更新非常缓慢,从而影响训练速度和效果。因此,在深度学习中,有时会选择其他激活函数,如 ReLU(线性整流单元)等。
另外,偏置(bias)的引入是为了增加模型的表达能力。具体来说,在 Sigmoid 激活函数中,偏置的作用如下:
-
调整激活函数的输出:在神经网络中,激活函数(如 Sigmoid 函数)用于对节点的线性加权和进行非线性转换。偏置相当于一个常数值,可以使得激活函数的输出在整体上向上或向下平移。这样,激活函数可以在不同区域内保持对输入的敏感性,提高模型的拟合能力。
-
提高模型的灵活性:加入偏置后,神经网络可以学习到更复杂的表示。偏置参数使神经网络能够在没有输入(或输入为零)时产生非零输出。如果没有偏置,即使权重参数不同,神经元在输入为零时的输出也将相同。因此,引入偏置为神经网络提供了额外的自由度,使其能够更好地拟合复杂的数据。
以 Sigmoid 函数为例,一个神经元的输出可以表示为:
output = sigmoid(w1 * x1 + w2 * x2 + ... + wn * xn + b)
这里,w1、w2、...、wn 是输入数据(x1、x2、...、xn)对应的权重,b 是偏置。通过调整偏置 b 的值,可以使 Sigmoid 函数的输出整体上升或下降,从而改变神经元的激活阈值。这使神经网络能够更好地适应不同的数据分布,提高模型的泛化能力。
FAQs
梯度与函数导数的关系?
梯度与导数密切相关,但它们有一些区别。对于单变量函数(即只有一个自变量的函数),梯度就是导数。导数表示该函数在某一点处的切线斜率。对于多变量函数(即有多个自变量的函数),梯度是一个向量,包含了函数在某一点处沿着各个坐标轴方向的偏导数。
换句话说,梯度是一个向量,它将多个偏导数组合在一起,描述了多变量函数在各个方向上的变化情况。梯度的方向是函数在该点处变化最快的方向,梯度的大小表示函数在该点处的变化速率。
总结一下:
-
对于单变量函数,梯度就是导数。
-
对于多变量函数,梯度是一个包含所有偏导数的向量。
AI Advisor公众号:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号