傅立叶变换(Fourier Transform)
欧拉公式

注1:这里的j为虚部,即j2 = -1
注2:欧拉公式的证明详见https://math.fandom.com/zh/wiki/Euler_%E5%85%AC%E5%BC%8F?variant=zh
欧拉公式描述的是一个随着时间变化,在复平面上做圆周运动的
推导可以得到:

傅里叶变换
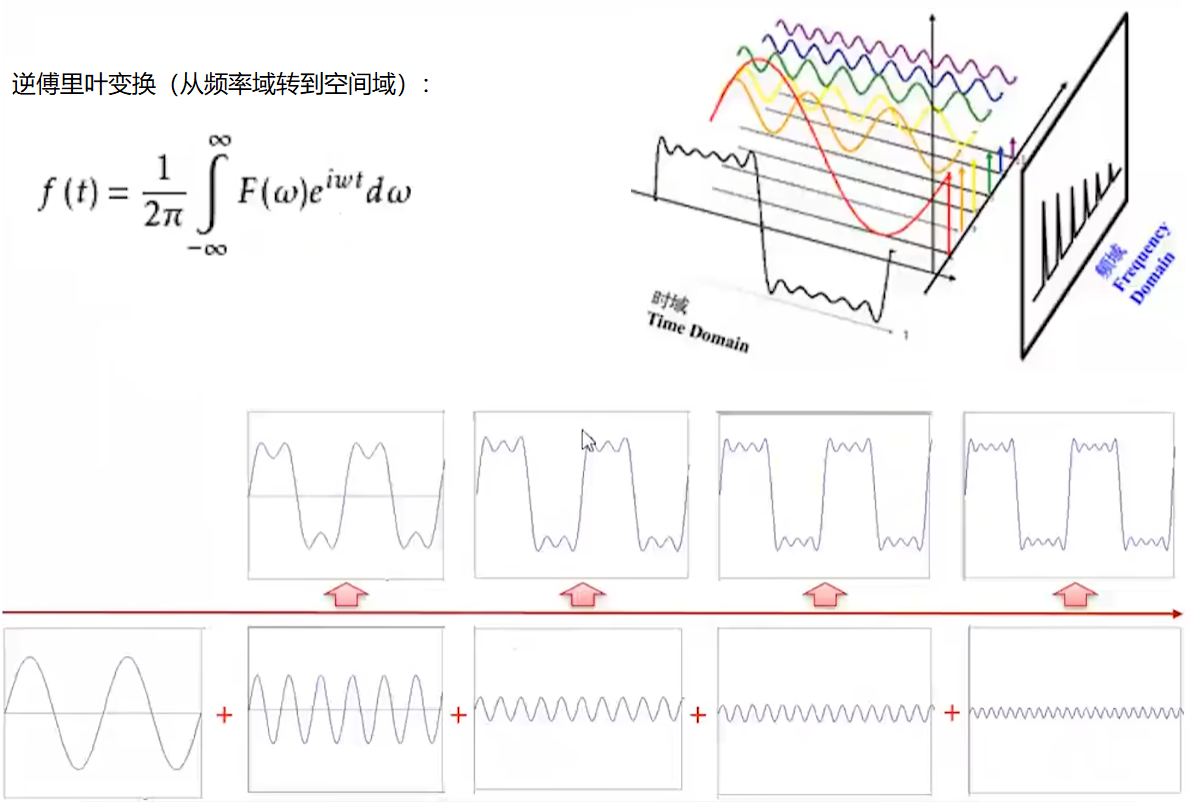
傅里叶变换描述的就是一系列点的运动叠加的效应

以逆傅里叶变换来理解这个过程
$F(w)$为当值为$w$时的频域值,$F(w) \cdot e^{iwt} $为单个圆上的点旋转随时间的展开(即:单个正弦波)
对$w$从$-\infty$到$+\infty$对$F(w) \cdot e^{iwt} $进行积分,表示将各个正弦波进行叠加求和,最后乘以一个$\frac{1}{2\pi } $的系数
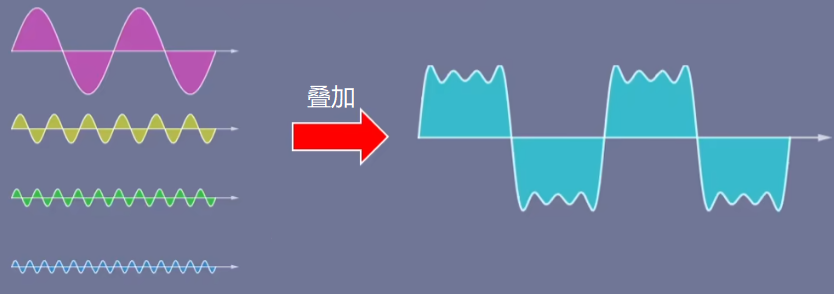
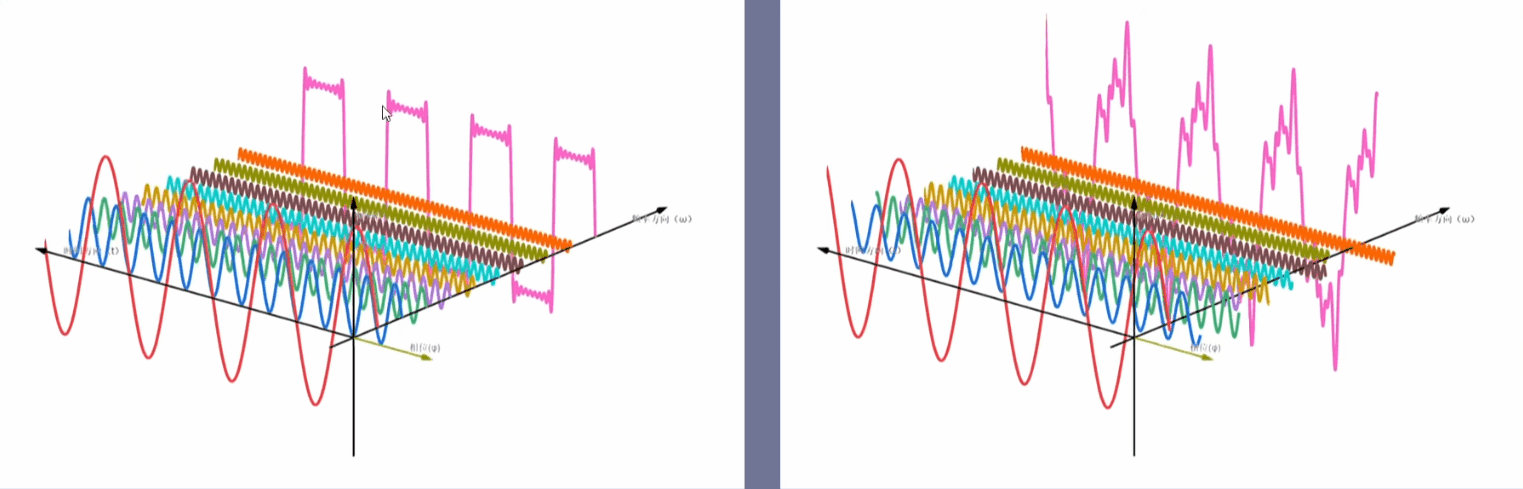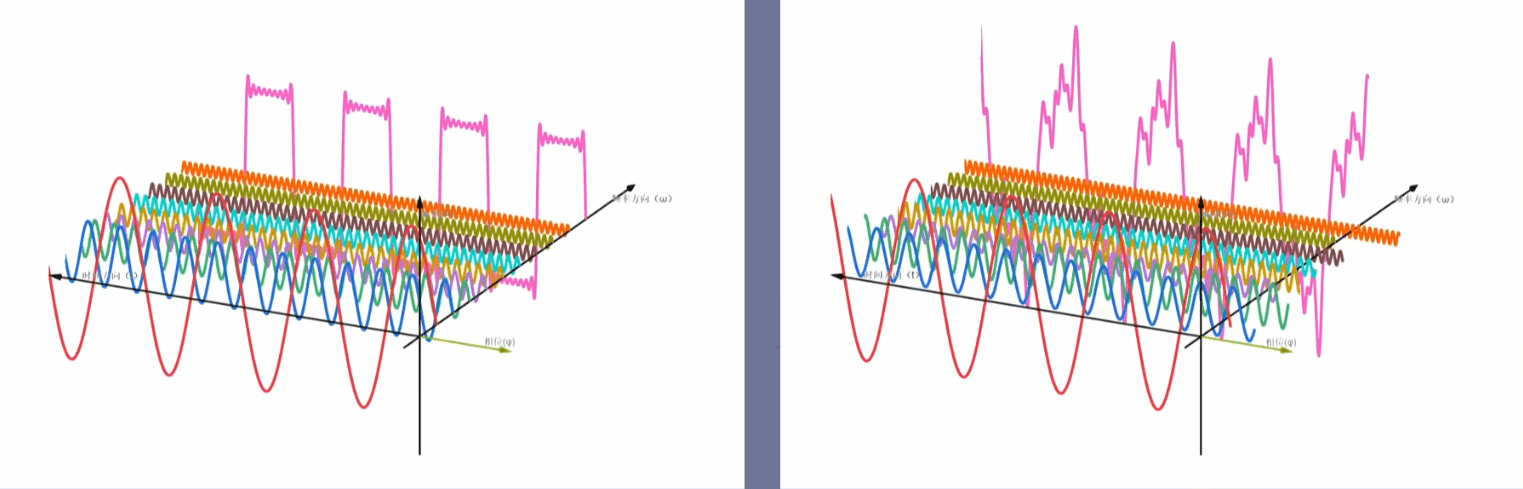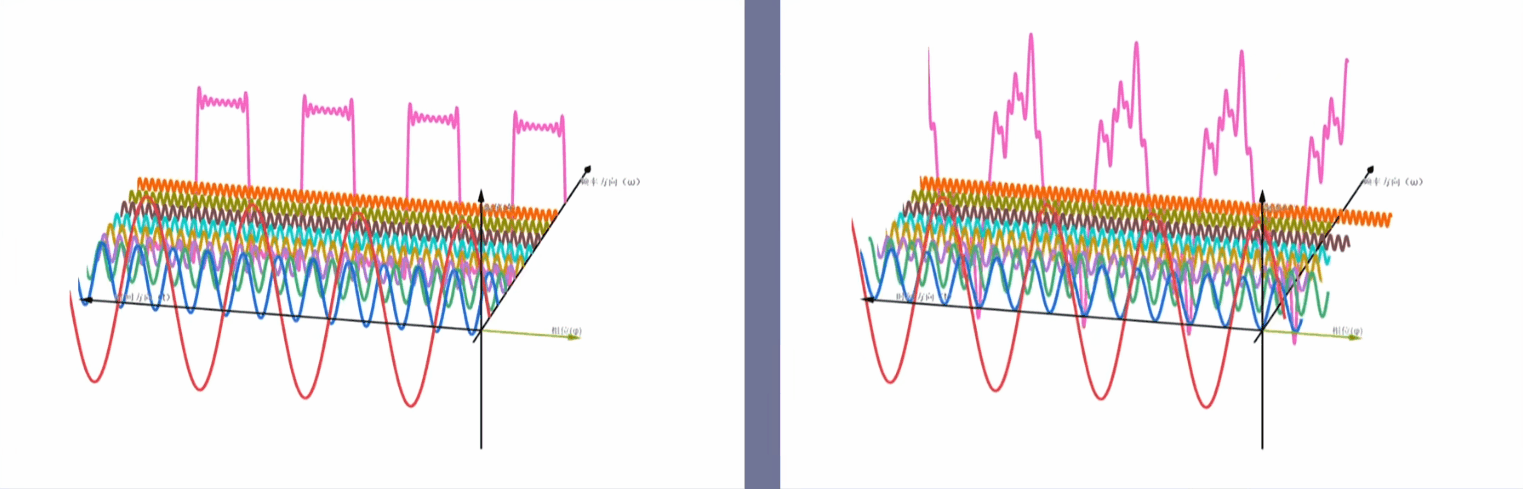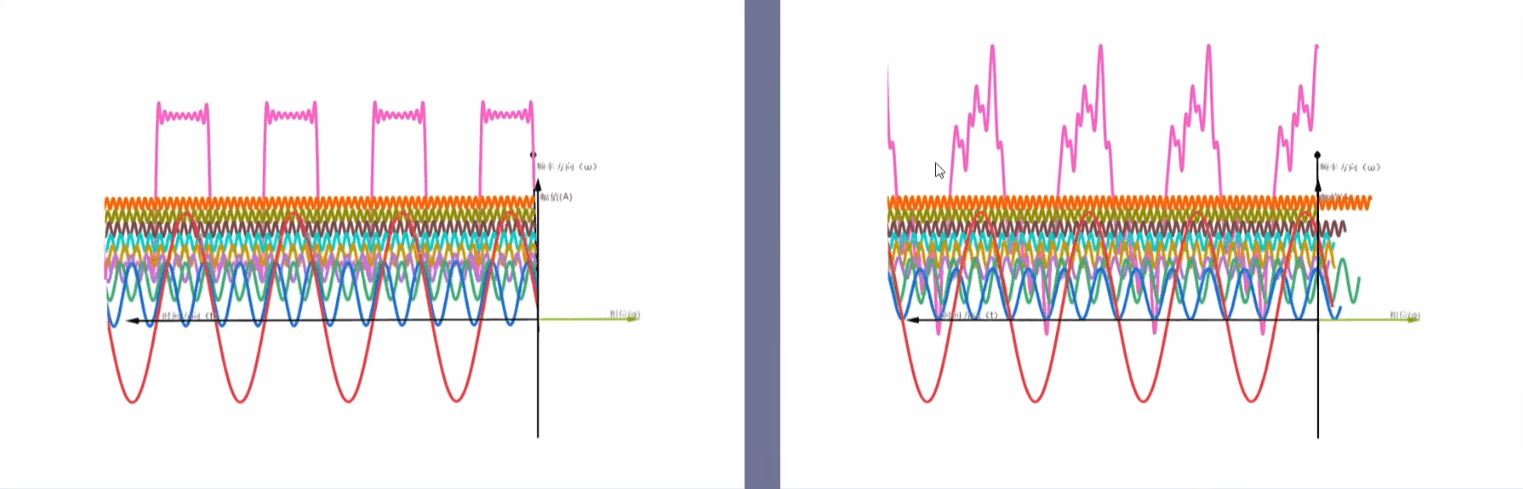
一个信号是由不同频率不同相位的正弦信号叠加而成 注:正弦信号包括正弦波和余弦波,正弦波和余弦波只是相差$\frac{\pi }{2} $个相位

时域信号与频域信号

左图为初相位为0的三角函数叠加 ----- 右图为初相位不为0的三角函数叠加
傅立叶变换(FT,Fourier Transform)

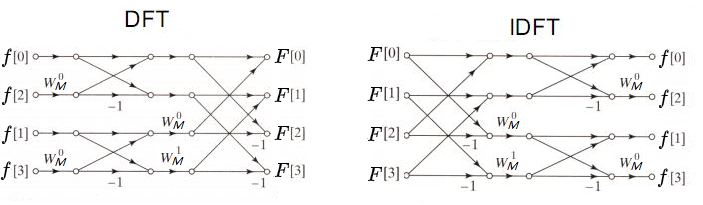
离散傅立叶变换(DFT,Discrete Fourier Transform)

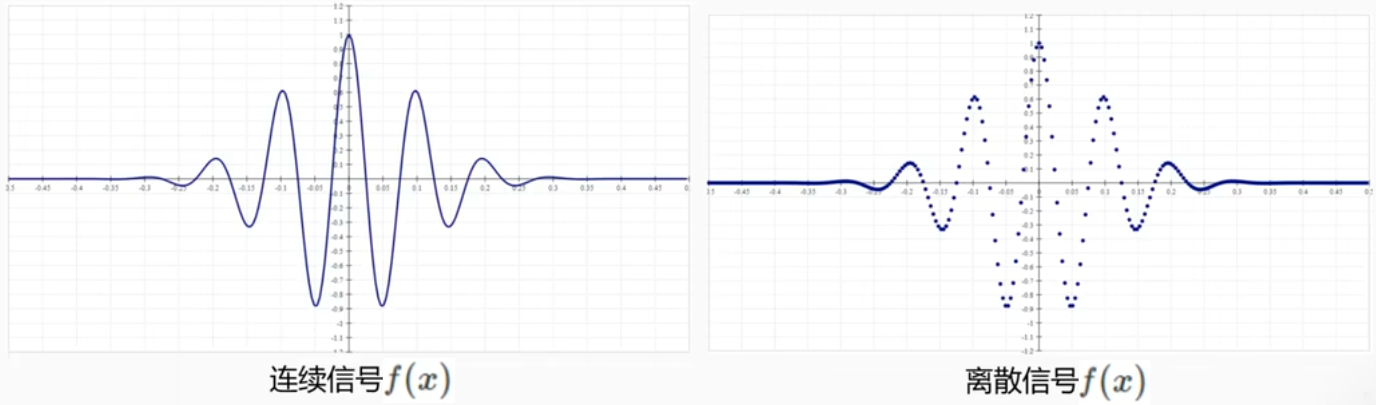
以样本数为4为例(即M=4),来进行说明:
$F(0) = \sum_{x=0}^{3} f(x)\cdot e^{0} =\sum_{x=0}^{3} f(x)= f(0)+f(1)+f(2)+(3)$
$F(1) = \sum_{x=0}^{3} f(x)\cdot e^{\frac{-j\cdot2\pi\cdot x}{4} } =\sum_{x=0}^{3} f(x)\cdot e^{-j\cdot\frac{\pi}{2}\cdot x }= f(0)+f(1)\cdot e^{-j\cdot\frac{\pi}{2} }+f(2)\cdot e^{-j\cdot \pi }+f(3)\cdot e^{-j\cdot\frac{3\pi}{2} }$
$F(2) = \sum_{x=0}^{3} f(x)\cdot e^{\frac{-j\cdot4\pi\cdot x}{4} } =\sum_{x=0}^{3} f(x)\cdot e^{-j\cdot\pi\cdot x }= f(0)+f(1)\cdot e^{-j\cdot\pi }+f(2)\cdot e^{-j\cdot 2\pi }+f(3)\cdot e^{-j\cdot3\pi }$
$F(3) = \sum_{x=0}^{3} f(x)\cdot e^{\frac{-j\cdot2\pi\cdot 3\cdot x}{4} } =\sum_{x=0}^{3} f(x)\cdot e^{-j\cdot\frac{3\pi}{2}\cdot x }= f(0)+f(1)\cdot e^{-j\cdot\frac{3\pi}{2} }+f(2)\cdot e^{-j\cdot 3\pi }+f(3)\cdot e^{-j\cdot\frac{9\pi}{2} }$
用矩阵表示,则为:
$\begin{bmatrix}
F(0) & F(1) & F(2) &F(3)
\end{bmatrix}
=
\begin{bmatrix}
f(0) & f(1) & f(2) &f(3)
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & e^{-j\cdot \frac{\pi}{2} } & e^{-j\cdot \pi } & e^{-j\cdot\frac{3\pi}{2} }\\
1 & e^{-j\cdot\pi } & e^{-j\cdot 2\pi } & e^{-j\cdot3\pi }\\
1 & e^{-j\cdot \frac{3\pi}{2} } & e^{-j\cdot 3\pi } & e^{-j\cdot\frac{9\pi}{2} }
\end{bmatrix}$
其中矩阵$A$为一个对称阵:
$\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & e^{-j\cdot \frac{\pi}{2} } & e^{-j\cdot \pi } & e^{-j\cdot\frac{3\pi}{2} }\\
1 & e^{-j\cdot\pi } & e^{-j\cdot 2\pi } & e^{-j\cdot3\pi }\\
1 & e^{-j\cdot \frac{3\pi}{2} } & e^{-j\cdot 3\pi } & e^{-j\cdot\frac{9\pi}{2} }
\end{bmatrix}$
利用欧拉公式$e^{-j\theta } = cos\theta -j \cdot sin \theta $可知
$e^{-j\cdot \frac{\pi}{2} }=-j$
当$u$为奇数时,$e^{-j\cdot u \pi }=-1$,$e^{-j\cdot \frac{(2u+1)\pi}{2} }=e^{-j\cdot u \pi } \cdot e^{-j\cdot \frac{\pi}{2} }=-1 \cdot -j = j$
当$u$为偶数时,$e^{-j\cdot u \pi }=1$,$e^{-j\cdot \frac{(2u+1)\pi}{2} }=e^{-j\cdot u \pi } \cdot e^{-j\cdot \frac{\pi}{2} }=1 \cdot -j =-j$
矩阵$A$化简为:
$\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & -j & -1 & j\\
1 & -1 & 1 & -1\\
1 & j & -1 & -j
\end{bmatrix}$
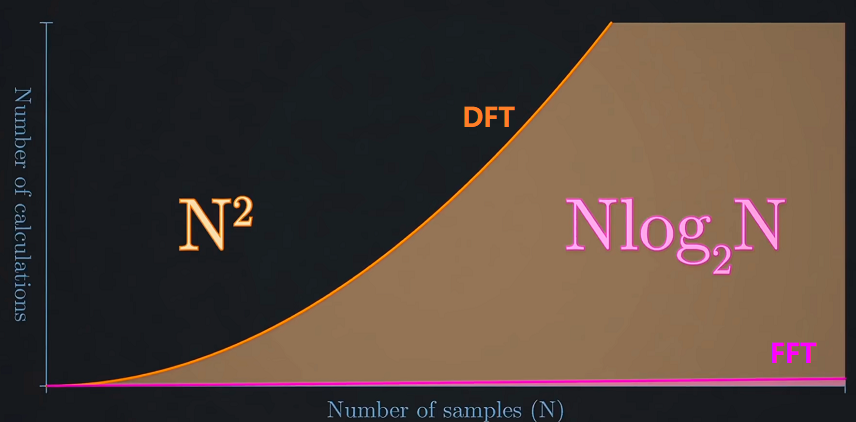
快速傅立叶变换(FFT,Fast Fourier Transform)
DFT的算法复杂度为$O(n^2)$,FFT算法对其进行了改善,在得到一样结果基础上,大大降低了其计算量,将算法的复杂度优化到$O(n\cdot log_{2} n)$
FFT必须要求元素的数量为$2^n$个,实际上可以通过添加0来补全为$2^n$个,从而可以计算任意个元素的FFT 注:添加0之后,只会让频率阈的幅度谱更加平滑

主流有两种实现方式:
① 库利-图基FFT算法(Cooley–Tukey FFT algorithm) // 基于蝶形运算的递归实现方式
② 威诺格拉德FFT算法(Winograd FFT algorithm) // 基于多项式乘法的递归实现方式
原始Cooley-Tukey算法的基本思路是采用递归的方法进行计算,但在算法实现会将显式的递归算法改写为非递归的形式,以便让该算法也可以在gpu上执行 注:gpu上不允许执行递归函数
Cooley-Tukey算法
下面以一维DFT来讲解Cooley-Tukey算法的非递归实现方式:
$F(0) = f(0)+f(1)+f(2)+(3) = f(0)+f(2)+f(1)+(3)= \left [ f(0)+f(2) \right ] +\left [ f(1)+(3) \right ] \cdot e^{0} $
$F(1) = f(0)+f(2)\cdot e^{-j\cdot \pi }+f(1)\cdot e^{-j\cdot\frac{\pi}{2} }+f(3)\cdot e^{-j\cdot\frac{3\pi}{2} } = f(0)-f(2)+\left [ f(1)+f(3)\cdot e^{-j\cdot\pi } \right ]\cdot e^{-j\cdot\frac{\pi}{2} } = \left [ f(0)-f(2) \right ]+ \left [ f(1)-f(3) \right ]\cdot e^{-j\cdot\frac{\pi}{2} } $
$F(2) = f(0)+f(2)\cdot e^{-j\cdot 2\pi }+f(1)\cdot e^{-j\cdot\pi }+f(3)\cdot e^{-j\cdot3\pi } = f(0)+f(2)+\left [ f(1)+f(3)\cdot e^{-j\cdot2\pi } \right ] \cdot e^{-j\cdot\pi } = \left [ f(0)+f(2) \right ]+ \left [ f(1)+f(3) \right ] \cdot e^{-j\cdot\pi }$
$F(3) = f(0)+f(2)\cdot e^{-j\cdot 3\pi }+f(1)\cdot e^{-j\cdot\frac{3\pi}{2} }+f(3)\cdot e^{-j\cdot\frac{9\pi}{2} } =f(0)-f(2)+\left [ f(1)+f(3)\cdot e^{-j\cdot 3\pi } \right ]\cdot e^{-j\cdot\frac{3\pi}{2} } = \left [ f(0)-f(2) \right ]+\left [ f(1)-f(3) \right ]\cdot e^{-j\cdot\frac{3\pi}{2} }$
将奇数项(Odd)和偶数项(Even)分离,得到:
$F(0) = \left [ f(0)+f(2) \right ]+\left [ f(1)+f(3) \right ] \cdot 1$
$F(2) = \left [ f(0)+f(2) \right ]+\left [ f(1)+f(3) \right ] \cdot -1$
$F(1) = \left [ f(0)-f(2) \right ]+\left [ f(1)-f(3) \right ] \cdot -j$
$F(3) = \left [ f(0)-f(2) \right ]+\left [ f(1)-f(3) \right ] \cdot j$
将奇数项(Odd)和偶数项(Even)分离,将序列长为$M$的DFT分割为两个长为$M/2$的子序列的DFT,公式推导如下:
$F(u)= \sum_{x=0}^{M-1} f(x)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot x}{M} }$
$F(u)= \sum_{r=0}^{\frac{M}{2} -1} f(2r)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot 2r}{M} } + \sum_{r=0}^{\frac{M}{2} -1} f(2r+1)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot (2r+1)}{M} }$
$F(u)= \sum_{r=0}^{\frac{M}{2} -1} f_1(r)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot r}{M/2} } + \sum_{r=0}^{\frac{M}{2} -1} f_2(r)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot (r+1/2)}{M/2} } $
$F(u)= \sum_{r=0}^{\frac{M}{2} -1} f_1(r)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot r}{M/2} } + \sum_{r=0}^{\frac{M}{2} -1} f_2(r)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot r}{M/2} } \cdot e^{\frac{-j\cdot 2\pi \cdot u }{M} } $
$F(u)= \sum_{r=0}^{\frac{M}{2} -1} f_1(r)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot r}{M/2} } + {\color{Red}{ e^{-j\cdot 2\pi \cdot \frac{u}{M} }} } \cdot \sum_{r=0}^{\frac{M}{2} -1} f_2(r)\cdot e^{\frac{-j\cdot 2\pi \cdot u \cdot r}{M/2} }$
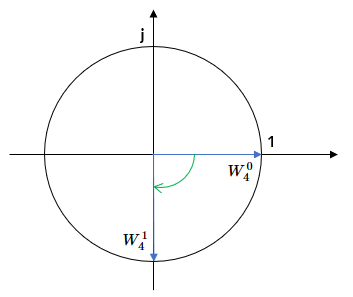
旋转因子(twiddle factor)
上面$W_{M}^{u} = \color{Red}{ e^{-j\cdot 2\pi \cdot\frac{u}{M} } }$为旋转因子(twiddle factor)
用欧拉公式展开得:$W_{M}^{u} =cos2\pi \cdot \frac{u}{M} - j \cdot sin 2\pi \cdot \frac{u}{M}$
几何意义:向量$(1,0)$按照顺时针进行旋转,$W_{M}^{u}$表示旋转$u$个$W_{M}^{1}$角度

$W_{M}^{2} = W_{M}^{1} * W_{M}^{1}$
$W_{M}^{3} = W_{M}^{1} * W_{M}^{1}* W_{M}^{1} = W_{M}^{2} * W_{M}^{1}$
$W_{M}^{4} = W_{M}^{1} * W_{M}^{1}* W_{M}^{1} * W_{M}^{1} = W_{M}^{2} * W_{M}^{2} = W_{M}^{3} * W_{M}^{1}$
。。。 。。。
旋转因子的性质:
① $W_{M}^{0} = 1$
② 周期性,$W_M$具有周期$M$,即:$W_{M}^{u+M} = W_{M}^{u}$
③ 对称性,即:$W_{M}^{u+\frac{M}{2}} = W_{M}^{u}$
④ 若$m$是$M$的约数,$W_{M}^{mu} = W_{\frac{M}{m}}^{u}$
分解得到的2个子序列的DFT为:
$\begin{cases}
F(r) \space \space\space\space\space\space\space\space\space\space\space\space\space =f_1(r) + W_{M}^{u} \cdot f_2(r)
\\
F(r+M/2) = f_1(r) - W_{M}^{u} \cdot f_2(r)
\end{cases}$
其中$r=0, 1, 2, ... , M/2 -1$
示例图如下:
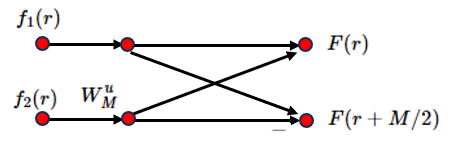
4个元素蝶形运算
以上使用蝶形运算可表示为:
上面为4个元素,即$M=4$,所以
$W_{M}^{0} = W_{4}^{0} = e^{-j\cdot 2\pi \cdot\frac{0}{4} } = e^0 = 1$
$W_{M}^{1} = W_{4}^{1} = e^{-j\cdot 2\pi \cdot\frac{1}{4} } = e^{-j\cdot \frac{\pi}{2} } = -j$
8个元素蝶形运算
对于8个元素,将奇数项(Odd)和偶数项(Even)分离,注意这里是彻底分离,直到分离不能再分的状态(即:每个子序列中只有2个元素)
例如:0、1、2、3、4、5、6、7分离成0、2、4、6 || 1、3、5、7两个子序列,继续对两个子序列进行奇偶分离
得到:0、4 | 2、6 || 1、5 | 3、7四个子序列
用蝶形运算可表示为:

上面为8个元素,即$M=8$,所以
$W_{M}^{0} = W_{8}^{0} = e^{-j\cdot 2\pi \cdot\frac{0}{8} } = e^0 = 1$
$W_{M}^{1} = W_{8}^{1} = e^{-j\cdot 2\pi \cdot\frac{1}{8} } = e^{-j\cdot \frac{\pi}{4} } = cos\frac{\pi}{4} - j\cdot sin\frac{\pi}{4} = \frac{\sqrt{2} }{2} -\frac{\sqrt{2} }{2}j$
$W_{M}^{2} = W_{8}^{2} = e^{-j\cdot 2\pi \cdot\frac{2}{8} } = e^{-j\cdot \frac{\pi}{2} } = -j$
$W_{M}^{3} = W_{8}^{3} = e^{-j\cdot 2\pi \cdot\frac{3}{8} } = e^{-j\cdot \frac{3\pi}{4} } = cos\frac{3\pi}{4} - j\cdot sin\frac{3\pi}{4} = -\frac{\sqrt{2} }{2} -\frac{\sqrt{2} }{2}j$

展开得到:
$F(0)=[f(0)+f(4)]+[f(2)+f[6])+\left \{[f(1)+f(5)]+[f(3)+f(7)]\right \}$
$F(4)=[f(0)+f(4)]+[f(2)+f[6])-\left \{ [f(1)+f(5)]+[f(3)+f(7)]\right \}$
$F(2)=[f(0)+f(4)]-[f(2)+f[6])+\left \{[f(1)+f(5)]-[f(3)+f(7)]\right \}\cdot W_{8}^{2}$
$F(6)=[f(0)+f(4)]-[f(2)+f[6])-\left \{[f(1)+f(5)]-[f(3)+f(7)]\right \}\cdot W_{8}^{2}$
$F(1)=[f(0)-f(4)]+[f(2)-f(6)]\cdot W_{8}^{2} +\left \{ [f(1)-f(5)]+[f(3)-f(7)]\cdot W_{8}^{2}\right \} \cdot W_{8}^{1}$
$F(5)=[f(0)-f(4)]+[f(2)-f(6)]\cdot W_{8}^{2} -\left \{ [f(1)-f(5)]+[f(3)-f(7)]\cdot W_{8}^{2}\right \} \cdot W_{8}^{1}$
$F(3)=[f(0)-f(4)]-[f(2)-f(6)]\cdot W_{8}^{2} +\left \{ [f(1)-f(5)]-[f(3)-f(7)]\cdot W_{8}^{2}\right \} \cdot W_{8}^{3}$
$F(7)=[f(0)-f(4)]-[f(2)-f(6)]\cdot W_{8}^{2} -\left \{ [f(1)-f(5)]-[f(3)-f(7)]\cdot W_{8}^{2}\right \} \cdot W_{8}^{3}$
16个运算蝶形运算
对于16个元素,将奇数项(Odd)和偶数项(Even)彻底分离
例如:0、1、2、3、4、5、6、7、8、9、10、11、12、13、14、15分离成0、2、4、6、8、10、12、14 ||| 1、3、5、7、9、11、13、15两个子序列,继续对两个子序列进行奇偶分离
得到:0、4 、8、12 || 2、6、10、14 ||| 1、5、9、13 || 3、7、11、15四个子序列,继续对四个子序列进行奇偶分离
得到:0、8 | 4、12 || 2、10 | 6、14 ||| 1、9 | 5、13 || 3、11 | 7、15八个子序列
用蝶形运算可表示为:
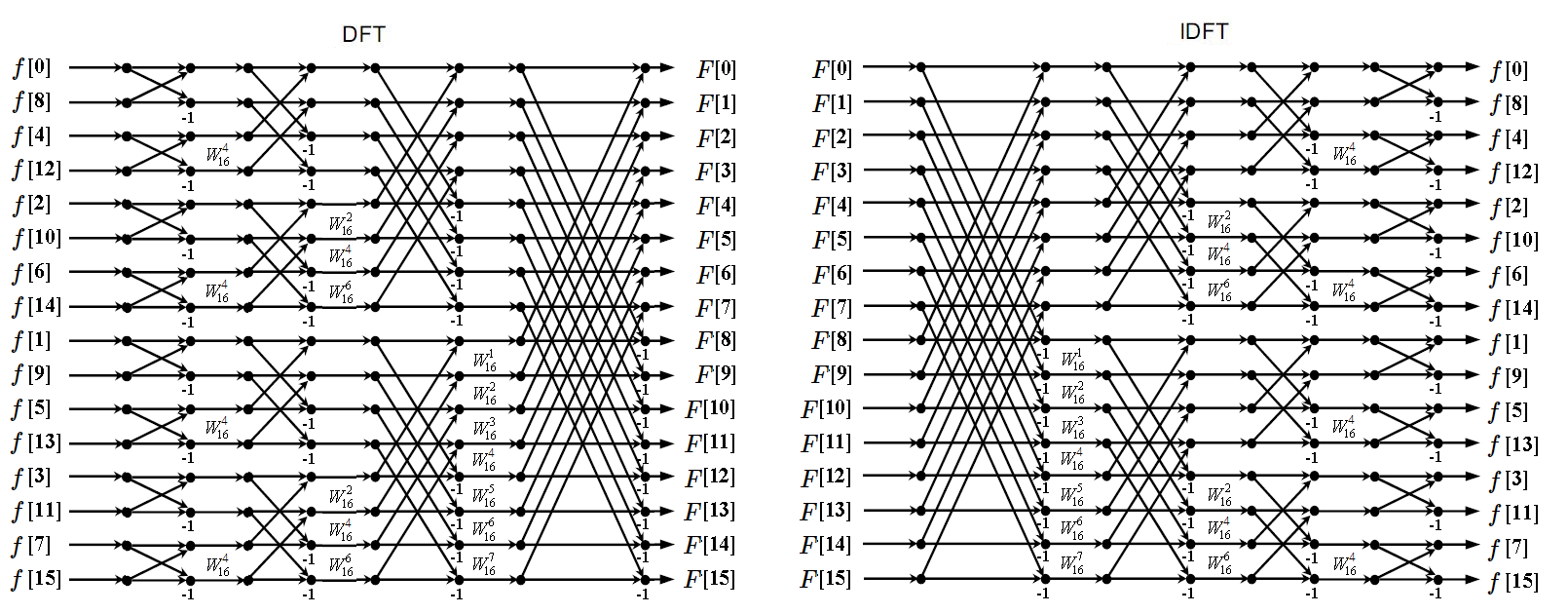
旋转因子如下:

奇偶解调
对于M个点,如何将奇数项(Odd)和偶数项(Even)彻底分离,快速分成2点 一组,作为第一级FFT变换的输入呢?
可使用码位倒置(即:将二进制反过来,又称位反转 -- Bit Reversal)方法来快速得到,以16个点的序列为例:
| 原序列(10进制) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 原序列(2进制) | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 码位倒置(2进制) | 0000 | 1000 | 0100 | 1100 | 0010 | 1010 | 0110 | 1110 | 0001 | 1001 | 0101 | 1101 | 0011 | 1011 | 0111 | 1111 |
| 码位倒置(10进制) | 0 | 8 | 4 | 12 | 2 | 10 | 6 | 14 | 1 | 9 | 5 | 13 | 3 | 11 | 7 | 15 |
图像的空间域到频率域之间的转换
空间域 --》DFT或FFT --》频率域 --》中心化 --》对数放大 --》傅立叶谱
傅立叶谱 --》指数还原 --》去中心化 --》频率域 --》IDFT或IFFT --》空间域


在频率域中,低频是信号中慢变化部分,对应图像的概貌(如大的轮廓);高频是信号中快速变化变化部分,对应图像的细节
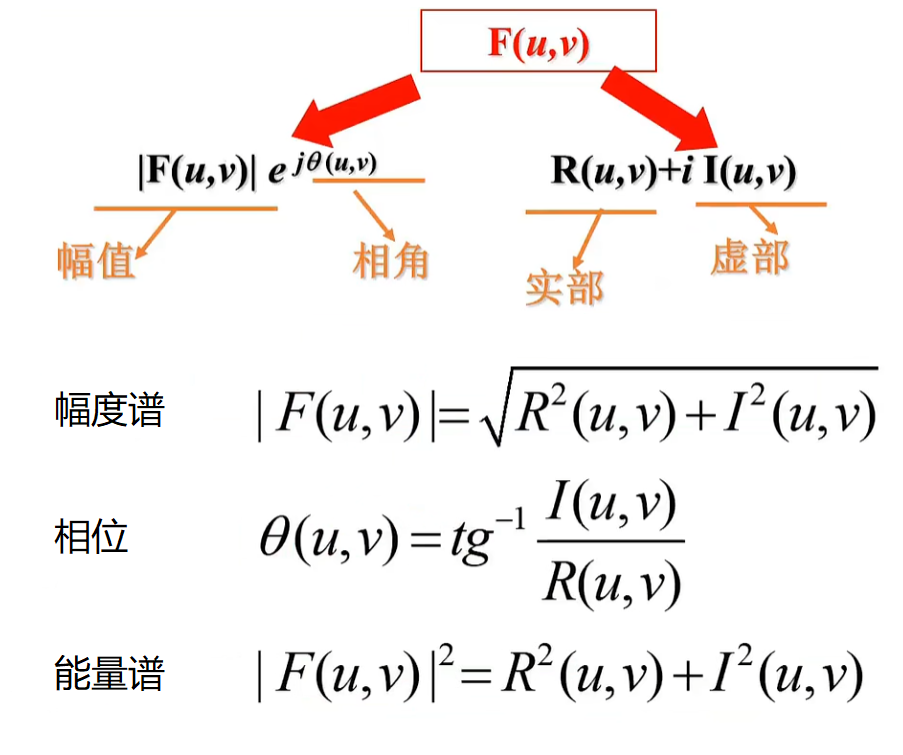

图像信号的傅里叶变换包含幅度与相位两部分:
幅度谱:具有较明显的信号结构特征,且易于解释。频率越低越靠近中心,频率越高越靠近边缘。但幅度本身只包含图像本身的周期结构,并不包含位置信息
相位谱:类似随机图案,一般难以解释,但包含图像里的位置信息,物体在空间的移动,相当于频域的相位移动,相位谱对于图像恢复具有同样重要的意义

对图像进行傅里叶变换,起始是一个二维离散傅里叶变换,图像的频率是指图像灰度变换的强烈程度,将二维图像由空间域变为频域后。
图像上的每个点的值都变成了复数,也就是所谓的复频域,通过复数的实部和虚部,可以计算出幅值和相位,计算幅值即对复数取模值,将取模值后的矩阵显示出来,即为其频谱图。
但是问题来了,复数取模后,数字有可能变的很大,远大于255,如果数据超过255,则在显示图像的时候会都当做255来处理,图像就成了全白色。
因此,一般会对模值再取对数,在在0~255的范围内进行归一化,这样才能够准确的反映到图像上,发现数据之间的差别,区分高频和低频分量,这也是进行傅里叶变换的意义。
基于傅里叶变换的滤波

参考



