一个mxn矩阵是一个m行n列的矩形数组。矩阵中每一项叫做矩阵的元素(Element),行数和列数指定了矩阵的维数。下面是一个2×3矩阵的例子:
[123456]
矩阵可以通过(i, j)进行索引,i是行,j是列,一共2行3列,因此叫做2×3矩阵的原因(2×3也叫做矩阵的维度,Dimension)。
矩阵的下标从1开始,所以第一行和第一列都用数字1。这与C语言中以0作为数组下标起点有所不同,矩阵没有0行0列。
矩阵相等
两个矩阵维数相同,且对应的各个元素也相同,则这两个矩阵相等。如下A矩阵与B矩阵相等,即A=B:
A=[15−23],B=[15−23]
矩阵转置
沿着矩阵M的对角线进行翻折,就得到其转置矩阵MT。mxn向量经过转置(transpose)后变成nxm向量,原来的行变成列,原来的列变成行。如下:
⎡⎢
⎢
⎢⎣123456789101112⎤⎥
⎥
⎥⎦T=⎡⎢⎣147102581136912⎤⎥⎦
矩阵转置的性质
(1) 对于任意矩阵M,其转置的转置为其自身。即:(MT)T=M
(2) 对于任意对角矩阵D,即:DT=D
矩阵数乘
矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量
2⋅[1234]=[2⋅12⋅22⋅32⋅4]=[2468]
矩阵数乘的性质
(1) 交换律
k⋅M=M⋅k
(2) 结合率
k1⋅(k2⋅M)=(k1⋅k2)⋅M
(3) 分配律
k⋅(A+B)=k⋅A+k⋅B
(k1+k2)⋅A=k1⋅A+k2⋅A
(4) 转置
(k⋅M)T=k⋅MT
矩阵加法
矩阵与矩阵之间的加法就是两个矩阵对应元素的加法运算。 注:两个矩阵需要维度相同
两个2×2矩阵相加:
[1234]+[5678]=[1+52+63+74+8]=[681012]
数学上是没有矩阵与标量相加的运算的,但是很多矩阵c++库则支持矩阵与标量的加法。
具体做法是将标量转变成一个相同维度的矩阵,然后再与矩阵进行相加。
2×2矩阵与标量相加:
[1234]+3=[1234]+[3333]=[1+32+33+34+3]=[4567]
矩阵加法的性质
(1) 交换律
A+B=B+A
(2) 结合律
(A+B)+C=A+(B+C)
(3) 转置
(A+B)T=AT+BT
矩阵减法
矩阵与矩阵之间的减法就是两个矩阵对应元素的减法运算。 注:两个矩阵需要维度相同
两个2×2矩阵相减:
[4216]−[2401]=[4−22−41−06−1]=[2−215]
与加法类似,矩阵与标量的减法的具体做法是将标量转变成一个相同维度的矩阵,然后再与矩阵进行相减。
2×2矩阵与标量相减:
[1234]−3=[1234]−[3333]=[1−32−33−34−3]=[−2−101]
方阵
行数和列数相同的矩阵称作方阵(square matrix)。常用的有2x2,3x3和4x4方阵。如下为一个3x3的方阵:
⎡⎢⎣m11m12m13m21m22m23m31m32m33⎤⎥⎦
对称矩阵
转置矩阵和自身相等的方阵,即:AT=A。如下为一个3x3的对称矩阵:
⎡⎢⎣12324−53−56⎤⎥⎦
反对称矩阵
转置矩阵和自身相等的方阵,即:AT=−A。如下为一个3x3的对称矩阵:
⎡⎢⎣02−1−20−4140⎤⎥⎦
对角矩阵
对角矩阵是所有非对角线元素都为0的方阵。一般记作D。如下为一个4x4的对角矩阵:
⎡⎢
⎢
⎢⎣3000010000−500002⎤⎥
⎥
⎥⎦
单位矩阵
单位矩阵(Identity Matrix)是一个对角线上的元素为1,其他都是0的N×N对角矩阵。n维单位矩阵记作In或者En。如下为一个4x4的单位矩阵:
⎡⎢
⎢
⎢⎣1000010000100001⎤⎥
⎥
⎥⎦
单位矩阵非常特殊:它是矩阵乘法的单位元(类似于数字1)。即:任意一个矩阵乘以单位矩阵,都将得到原矩阵。
M⋅I=I⋅M=M
矩阵与矩阵相乘
m×n矩阵与n×p矩阵才能相乘,得到新的m×p矩阵。即:只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。这表明乘法一般不具有交换性(A⋅B≠B⋅A)
⎡⎢
⎢
⎢⎣a11a12a21a22a31a32a41a42⎤⎥
⎥
⎥⎦⋅[b11b12b13b14b21b22b23b24]=⎡⎢
⎢
⎢⎣c11c12c13c14c21c22c23c24c31c32c33c34c41c42c43c44⎤⎥
⎥
⎥⎦
其中,cij=∑nk=1aik⋅bkj。
即:C矩阵第i行第j列的元素等于A矩阵第i行与B矩阵第j列所在向量的点积。用公式表示为:cij=¯ai⋅¯bj
例如:c24=a21⋅b14+a22⋅b24
一种更直观的写法是将矩阵B写在矩阵C的上面,目的是使A的行和B的列与C中对应的元素对齐。如下:
[b11b12b13b14b21b22b23b24]
⎡⎢
⎢
⎢⎣a11a12a21a22a31a32a41a42⎤⎥
⎥
⎥⎦ ⎡⎢
⎢
⎢⎣c11c12c13c14c21c22c23c24c31c32c33c34c41c42c43c44⎤⎥
⎥
⎥⎦
2×2矩阵相乘公式
[a11a12a21a22]⋅[b11b12b21b22]=[a11⋅b11+a12⋅b21a11⋅b12+a12⋅b22a21⋅b11+a22⋅b21a21⋅b12+a22⋅b22]
3×3矩阵相乘公式
⎡⎢⎣a11a12a13a21a22a23a31a32a33⎤⎥⎦⋅⎡⎢⎣b11b12b13b21b22b23b31b32b33⎤⎥⎦=⎡⎢⎣a11⋅b11+a12⋅b21+a13⋅b31a11⋅b12+a12⋅b22+a13⋅b32a11⋅b13+a12⋅b23+a13⋅b33a21⋅b11+a22⋅b21+a23⋅b31a21⋅b12+a22⋅b22+a23⋅b32a21⋅b13+a22⋅b23+a23⋅b33a31⋅b11+a32⋅b21+a33⋅b31a31⋅b12+a32⋅b22+a33⋅b32a31⋅b13+a32⋅b23+a33⋅b33⎤⎥⎦
2×2矩阵相乘示例
[1234]⋅[5678]=[1⋅5+2⋅71⋅6+2⋅83⋅5+4⋅73⋅6+4⋅8]=[19224350]
3×3矩阵相乘示例
⎡⎢⎣420081010⎤⎥⎦⋅⎡⎢⎣421204942⎤⎥⎦=⎡⎢⎣4⋅4+2⋅2+0⋅94⋅2+2⋅0+0⋅44⋅1+2⋅4+0⋅20⋅4+8⋅2+1⋅90⋅2+8⋅0+1⋅40⋅1+8⋅4+1⋅20⋅4+1⋅2+0⋅90⋅2+1⋅0+0⋅40⋅1+1⋅4+0⋅2⎤⎥⎦=⎡⎢⎣2081225434204⎤⎥⎦
矩阵乘法的性质
(1) 矩阵乘法不满足交换律。即:AB≠BA
(2) 矩阵乘法满足结合律。即(AB)C=A(BC) 注1:假设A、B、C的维数使其乘法有意义。 注2:如果(AB)C有意义,那么A(BC)一定有意义。
扩展到多个矩阵的情况,也有:ABCDEF=((((AB)C)D)E)F=A((((BC)D)E)F)=(AB)(CD)(EF) 注:所有括法都能计算出正确结果,但有些组中标量乘法更少。寻找使标量乘法最少的问题,称为矩阵链问题。
(3) 矩阵乘法也满足与标量或向量的结合律
(kA)B=k(AB)=A(kB)
(¯vA)B=¯vAB
(4) 分配率
(A+B)C=AC+BC
C(A+B)=CA+CB
(5) 反序定律:矩阵积的转置相当于先转置矩阵然后以相反的顺序乘
(AB)T=BTAT
扩展到多个矩阵的情况,也有:(M1M2⋯Mn−1Mn−2)T=Mn−2TMn−1T⋯M2TM1T
(Ak)T=(AT)k k为整数
矩阵的行列式
只有方阵才有行列式(为一个标量),非方阵矩阵的行列式是未定义的。
方阵A的行列式记作∣A∣或“detA”。
2×2矩阵行列式公式
|A|=∣∣∣a11a12a21a22∣∣∣=a11⋅a22−a12⋅a21
按照主对角线减去副对角线规律为:
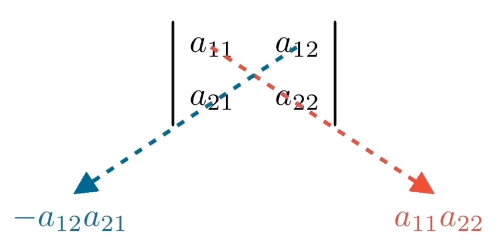
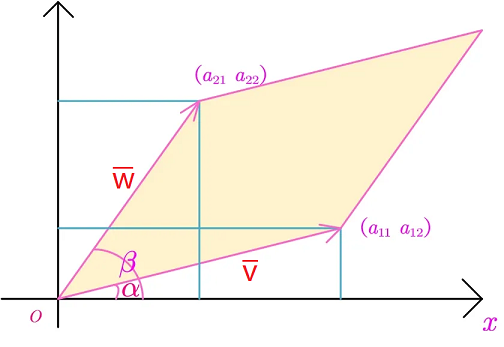
2阶行列式几何意义
行列式的值等于第1个行向量¯v与第2个行向量¯w为两边的平行四边形的有符号的面积。注:也可以使用第1个列向量与第2个列向量
当对¯v到¯w使用右手螺旋法则,如果大拇指方向朝向屏幕外,则面积为正;当大拇指方向朝向屏幕内,则面积为负。
|A|=∣∣∣¯v¯w∣∣∣=∣∣∣a11a12a21a22∣∣∣=a11⋅a22−a12⋅a21
3×3矩阵行列式公式
|A|=∣∣
∣∣a11a12a13a21a22a23a31a32a33∣∣
∣∣=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a21⋅a32−a13⋅a22⋅a31−a12⋅a21⋅a33−a11⋅a23⋅a32=a11⋅(a22⋅a33−a23⋅a32)+a12⋅(a23⋅a31−a21⋅a33)+a13⋅(a21⋅a32−a22⋅a31)
按照主对角线减去副对角线规律为:
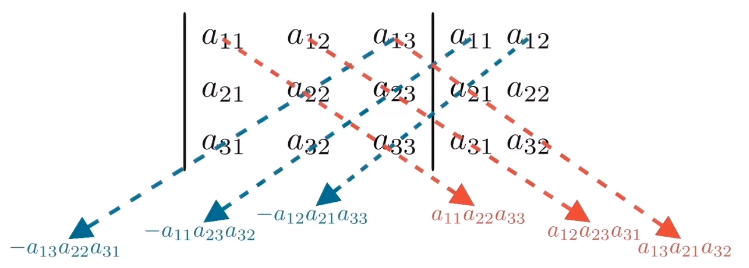
三元组积
如果将3x3阶矩阵的行解释为3个向量,那么矩阵的行列式等于这些向量的三元组积
∣∣
∣∣¯a¯b¯c∣∣
∣∣=∣∣
∣
∣∣axayazbxbybzcxcycz∣∣
∣
∣∣=ax⋅by⋅cz+ay⋅bz⋅cx+az⋅bx⋅cy−az⋅by⋅cx−ay⋅bx⋅cz−ax⋅bz⋅cy=(ay⋅bz−az⋅by)⋅cx+(az⋅bx−ax⋅bz)⋅cy+(ax⋅by−ay⋅bx)⋅cz=(¯aׯb)⋅¯c
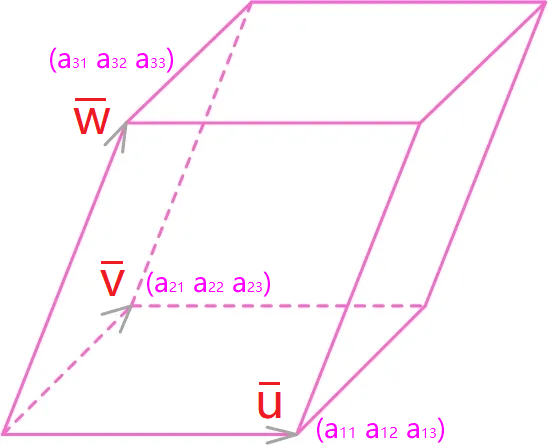
3阶行列式几何意义
行列式的值等于第1个行向量¯u、第2个行向量¯v和第3个行向量¯w为棱边的平行六面体的有符号的体积。注:也可以使用第1个列向量、第2个列向量与第3个列向量
当对¯u到¯v使用右手螺旋法则,如果大拇指方向与¯w在大拇指方向的分量朝向一致,则面积为正;朝向相反,则面积为负。
|A|=∣∣
∣∣¯u¯v¯w∣∣
∣∣=∣∣
∣∣a11a12a13a21a22a23a31a32a33∣∣
∣∣
4x4矩阵行列式公式

4阶不能按照主对角线减去副对角线规律,该规律下计算式只有8项(如下),但实际它的计算式有24项
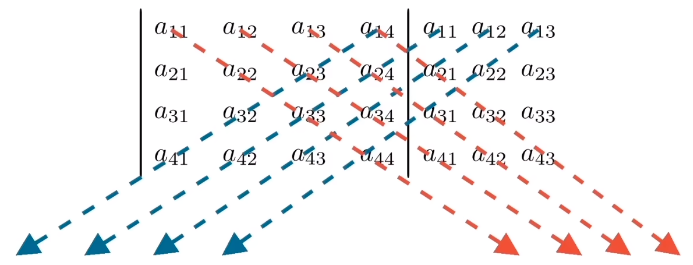
nxn矩阵行列式公式
n阶方阵A=(aiaj),其定义为:
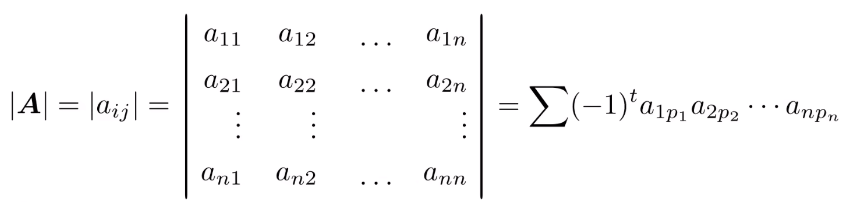
其中:p1p2⋅⋅⋅pn是数字1到n的全排列(全排列即不遗漏不重复地将所有数字排在一起,n个不同数的全排列种数有n!个)
t为全排列p1p2⋅⋅⋅pn的逆序数
∑表示对1,2,⋅⋅⋅,n的所有全排列p1p2⋅⋅⋅pn求和
----------------------------------逆序数说明-----------------------------------------
2431中的逆序有(2,1),(4,3),(4,1),(3,1),即其逆序数为4,它是一个偶排列。
45321中的逆序有(4,3),(4,2),(4,1),(5,3),(5,2),(5,1),(3,2),(3,1),(2,1),即其逆序数为9,它是一个奇排列。
排列1,2,...,n中没有逆序,即逆序数为零,因而它是偶排列。
-----------------------------------------------------------------------------------------
更多信息详见:马同学图解数学 -- 如何计算n阶行列式(如何理解全排列,逆序数及行列式的定义)
行列式的性质
(1) 矩阵积的行列式等于矩阵行列式的积:∣A⋅B∣=∣A∣⋅∣B∣
(2) 这可以扩展到多个矩阵的情况:∣A1A2⋅⋅⋅An∣=∣A1∣⋅∣A2∣⋅⋅⋅∣An∣
(3) 矩阵转置的行列式等于原矩阵的行列式:∣AT∣=∣A∣
(4) 行列式的任意行或列全为0,那么它的值等于0
(5) 行列式有两行或列元素完全相同,那么它的值等于0
(6) 交换行列式的任意两行或两列,它的值变负
(7) 用数k乘行列式某一行或某一列中所有元素,等于用k乘此行列式
(8) 任意行或列的k倍(k≠0)加到另一行或列上不会改变行列式的值
(9) 行列式中某一行(列)的每个元素是两数之和,则此行列式可拆分为两个相加的行列式,该性质也可以称为行列式的加法

更多详见:行列式的运算性质
余子式和代数余子式
n阶行列式∣A∣,除去第i行和第j列后剩下的行列式∣Aij∣,称为元素aij的余子式。
考虑第i行和第j列符号的余子式,称为元素aij的代数余子式:cij=(−1)i+j∣Aij∣
从矩阵中任意选择一行或一列,对该行或列中的每个元素,都乘以对应的代数余子式,乘积的和就是矩阵的行列式。例如选择行i,行列式的计算过程如下公式:
∣A∣=∑nj=1aijcij=∑nj=1aij(−1)i+j∣Aij∣=∑nj=1(−1)i+jaij∣Aij∣
利用代数余子式计算4x4行列式
∣∣
∣
∣
∣∣a11a12a13a14a21a22a23a24a31a32a33a34a41a42a43a44∣∣
∣
∣
∣∣=a11∣∣
∣∣a22a23a24a32a33a34a42a43a44∣∣
∣∣−a21∣∣
∣∣a12a13a14a32a33a34a42a43a44∣∣
∣∣+a31∣∣
∣∣a12a13a14a22a23a24a42a43a44∣∣
∣∣−a41∣∣
∣∣a12a13a14a22a23a24a32a33a34∣∣
∣∣
余子式的性质
当i≠j时,则aj1⋅∣Ai1∣+aj2⋅∣Ai2∣+⋅⋅⋅+ajn⋅∣Ain∣=0,或a1j⋅∣A1i∣+a2j⋅∣A2i∣+⋅⋅⋅+anj⋅∣Ani∣=0
当i=j时,则aj1⋅∣Ai1∣+aj2⋅∣Ai2∣+⋅⋅⋅+ajn⋅∣Ain∣=∣A∣,或a1j⋅∣A1i∣+a2j⋅∣A2i∣+⋅⋅⋅+anj⋅∣Ani∣=∣A∣
伴随矩阵
方阵A的代数余子式矩阵的转置矩阵为其伴随矩阵,记作adj(A),或A∗。
2×2方阵
[abcd]的伴随矩阵:
[d−b−ca]
3×3方阵
⎡⎢⎣a11a12a13a21a22a23a31a32a33⎤⎥⎦的伴随矩阵:
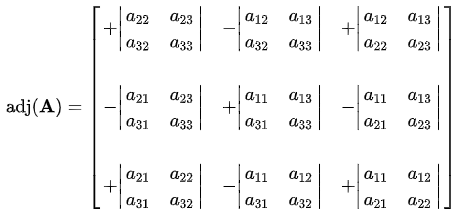
例如⎡⎢⎣−4−3302−204−1⎤⎥⎦的伴随矩阵为:
adj(A)=⎡⎢⎣6−2−291130−8−8⎤⎥⎦T=⎡⎢⎣690−21−8−213−8⎤⎥⎦
伴随矩阵的性质
(1) I∗=I
(2) A⋅A∗=A∗⋅A=∣A∣⋅I
(3) (A⋅B)∗=B∗⋅A∗
(4) (An)∗=(A∗)n
(5) (AT)∗=(A∗)T
(6) ∣A∗∣=∣A∣n−1
(7) (k⋅A)∗=kn−1⋅A∗
(8) (A∗)∗=∣A∣n−2⋅A
(9) 如果A是对称矩阵,那么其伴随矩阵也是对称矩阵;如果A是反对称矩阵,那么当n为偶数时,A的伴随矩阵也是反对称矩阵,n为奇数时则是对称矩阵。
逆矩阵
矩阵虽然没有类似于标量除法的运算,但可通过逆矩阵来实现矩阵乘法逆运算。
只有方阵才可能有逆矩阵。一个nxn矩阵M的逆矩阵也是一个nxn矩阵,用符号A−1表示。并非所有的方阵都有逆矩阵。
当一个方阵有逆矩阵,那么称它是可逆的或非奇异的;没有逆矩阵时,则它是不可逆的或奇异的。
矩阵A的逆矩阵为其伴随矩阵除以其行列式,公式如下:
A−1=A∗∣A∣
逆矩阵的性质
(1) 可逆矩阵(非奇异矩阵)的充分必要条件是其行列式不为0
(2) 对于任意可逆矩阵A,当且仅当列向量¯v为0时,¯v⋅A=0;或者当且仅当行向量¯v为0时,A⋅¯v=0。
(3) 当A、B为相同维度的可逆矩阵,则:(A⋅B)−1=B−1⋅A−1
(4) (k⋅A)−1=A−1k
(5) A⋅A−1=A−1⋅A=I
(6) (A−1)−1=A
(7) (AT)−1=(A−1)T
(8) (AB)−1=B−1A−1
扩展到多个矩阵的情况,也有:(M1M2⋯Mn−1Mn−2)−1=Mn−2−1Mn−1−1⋯M2−1M1−1
(9) (A∗)−1=(A−1)∗=A∣A∣
正交矩阵
若方阵A是正交矩阵,当且仅当A与它的转置矩阵AT的乘积等于单位矩阵I。
A⋅AT=I
由于A⋅A−1=I,因此,如果一个矩阵是正交的,当且仅当它的转置矩阵等于它的逆。
AT=A−1
以3x3方阵为例:
A=⎡⎢⎣m11m12m13m21m22m23m31m32m33⎤⎥⎦
A⋅AT=⎡⎢⎣m11m12m13m21m22m23m31m32m33⎤⎥⎦⋅⎡⎢⎣m11m21m31m12m22m32m13m23m33⎤⎥⎦=⎡⎢⎣100010001⎤⎥⎦
设向量¯u=[m11m12m13],¯v=[m21m22m23],¯w=[m31m32m33],则:
A=⎡⎢⎣¯u¯v¯w⎤⎥⎦
A⋅AT=⎡⎢⎣¯u¯v¯w⎤⎥⎦⋅[¯u¯v¯w]=⎡⎢⎣100010001⎤⎥⎦
则得到:
¯u⋅¯u=1,¯u⋅¯v=0,¯u⋅¯w=0
¯v⋅¯u=0,¯v⋅¯v=1,¯v⋅¯w=0
¯w⋅¯u=0,¯w⋅¯v=0,¯w⋅¯w=1
做出一些解释:
当且仅当一个向量是单位向量时,它与自身的点积结果是1。因此,仅当¯u,¯v,¯w是单位向量时,第1,5,9式成立。
当且仅当两个向量互相垂直时,它们的点积为0。因此,仅当¯u,¯v,¯w 互相垂直时,其他等式成立。
所以,若一个矩阵是正交的,它必须满足下列条件:
① 矩阵的每一行(列)都是单位向量
② 矩阵的所有行(列)互相垂直
正交矩阵的性质
(1) 任何向量¯v在正交变换A后模长不变,证明过程如下:
设列向量¯v=⎛⎜⎝xyz⎞⎟⎠
||¯v||=¯vT⋅¯v=(x,y,z)⋅⎛⎜⎝xyz⎞⎟⎠
设转换后的向量¯w=A⋅¯v
||¯w||=¯wT⋅¯w=(A⋅¯v)T⋅A⋅¯v=¯vT⋅AT⋅A⋅¯v=¯vT⋅¯v=||¯v||
(2) 任何两个向量¯v、¯w,在正交变换A后,向量之间的内积不变。
(3) 在各种变换中,有一种变换拥有良好的特性——它能使变换后的向量长度,向量之间的内积、距离、夹角等很多性质都不变,这种变换,我们称为正交变换,用于实施这种变换的矩阵,我们称为正交矩阵,这种变换的特性,我们称为正交变换的不变性。
参考
【官方双语/合集】线性代数的本质 - 系列合集(3Blue1Brown)
矩阵与矩阵乘法的来历(马同学图解数学)








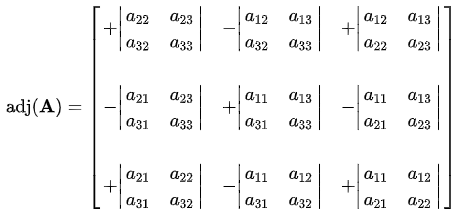






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· .NET10 - 预览版1新功能体验(一)
2015-09-30 vnc远程运行3D游戏