三维图形变换
是在二维方法基础上增加了对z坐标的考虑得到的。与二维变换类似,引入齐次坐标表示,即:三维空间中某点的变换可以表示成点的齐次坐标与四阶的三维变换矩阵相乘。
一、平移变换
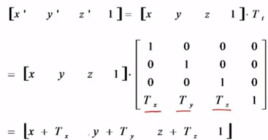
二.比例变换
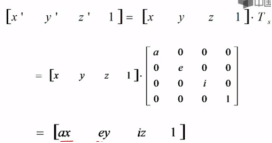
例如:对长方体进行比例变换,
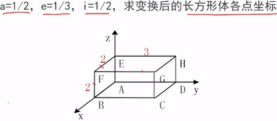
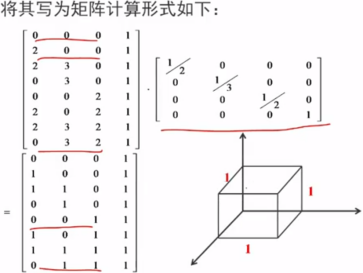

三、旋转变换
跟二维的相同
四、对称变换
有关于坐标平面、坐标轴的对称变换
(1)关于坐标平面的对称
绕哪个面变换,那个面不变
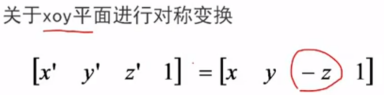
变换矩阵为:
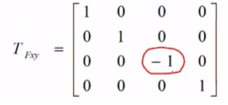 其它均类似
其它均类似
(2)关于坐标轴变换

6.2 投影变换
投影变换就是把三维物体投射到投影面上得到二维平面图形
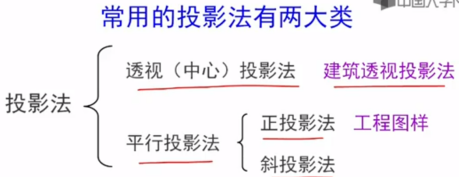
两种投影法的本质区别在于:透视投影的投影中心到投影面之间的距离是有限的;而另一个的距离是无限的。
一、中心(透视)投影
特点:投影线均通过投影中心,物体的投影视图由计算投影线与观察平面交点而得
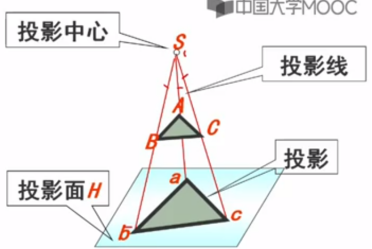
在投影中心相对投影面确定的情况下,空间的一个点在投影面上只存在唯一一个投影。
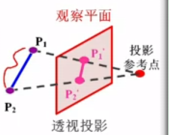
透视投影生成真实感视图,但不保证相关比例。
二、平行投影
1、把透视投影的中心移至无穷远处,则各投影线称为相互平行的直线,这种投影
2、分为正投影和斜投影
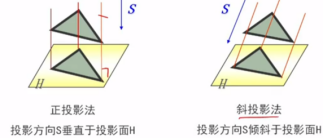
3、特点:保持物体的有关比例不变
三、平面集合投影的分类
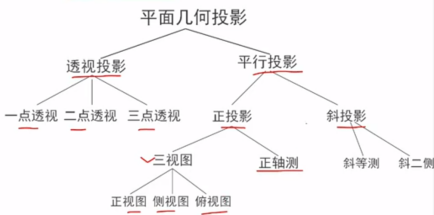
6.3 三视图
一、
1、根据投影面与坐标轴的夹角可分为两类:三视图和正轴侧图。
当投影面与某一坐标轴垂直时,得到的投影为三视图,这是投影方向与这个坐标轴的方向一致;否则,得到的投影为正轴侧图
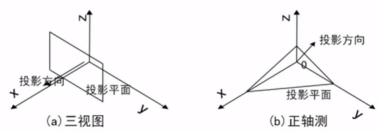
2、三视图包括主、侧、俯视图三种,投影面分别于x/y/z轴垂直
3、优点:反映形体的实际尺寸,工程制图中常用三视图来测量形体间的距离、角度以及相互位置关系。
4、缺点:三视图上只有物体一个面的投影,只有将三个图放在一起,才能综合物体的空间形状
二、三视图的计算
1>确定三维物体上个点的位置坐标
2>引入齐次坐标,求出所做变换相应的变换矩阵
3>将所做变换用矩阵表示,通过运算求得三维物体上各点经变换后的点坐标值
4>由变换后得到的二维点绘出三维物体投影后的三视图
三、
1>主视图:将三维物体xoz面(又称v面)做垂直投影,得到主视图

2>俯视图:将三维物体xoy面(又称h面)做垂直投影,得到俯视图
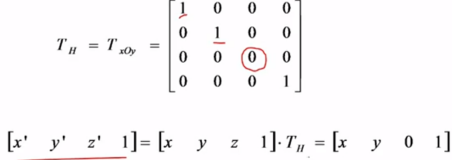
为了让其与主视图在一个平面内,让俯视图绕x轴旋转90°。并让两者产生一定的间距,让其再沿Z轴负方向移动些距离
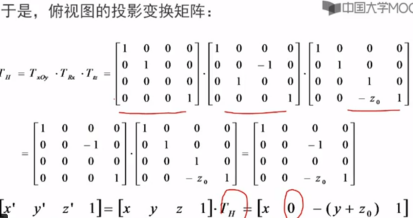
3>侧视图:将三维物体yoz面(又称w面)做垂直投影,得到侧视图
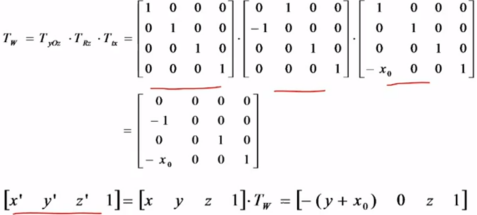
三种结果:

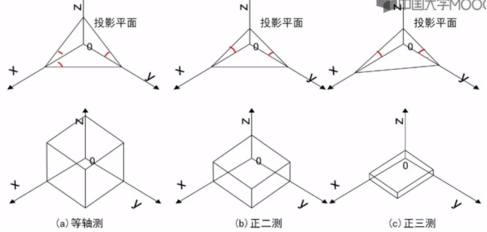
四、正轴侧
1、当投影面与三个坐标轴之间的夹角都相等时为等轴测
当投影面与两个坐标轴之间的夹角都相等时为正二测
投影面与三个坐标轴之间的夹角都不相等时为正三测
6.4 透视投影
一、
1、平行投影表示真实大小和形状的物体
透视投影表示真实看到的物体,比轴测图更富有立体感和真实感
2、透视投影是为了获得接近真实三维物体的视觉效果而在二维的纸或者画布平面上绘图或者渲染的一种方法,能逼真地反映形体的空间形象,也称为透视图。
是3D渲染的基本概念,也是3D程序设计的基础。
3、透视投影图是用中心投影法形成的,视点在有限远处。
4、透视基本原理:位于空间的任何一个点,它之所以能被人们的眼睛所看见,是因为从该点出发射出来的一条光线能够达到人们的眼睛。
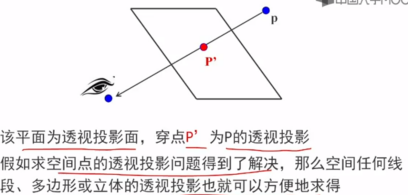
可以通过求出顶点的透视投影而获得空间任意立体的透视投影
二、
1、透视图的特点:
1>近大远小,近高远低
2>近长远短,近疏远密
3>互相平行的直线,其透视会交于一点
2、影响透视的两个因素:
1>视角:观察物体的角度
2>视距:眼睛到物体之间的距离
3、透视图的分类:
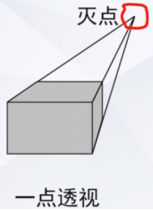
1>一点透视:也称平行透视。互相平行的直线汇聚成一个点,此点称为灭点,而且只有一个,所以称为一点透视。

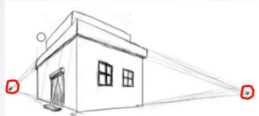
2>两点透视:称成角透视。通过物体旋转一定角度或者视点转动一定角度
其边线的延长线会相交于视平行线上立方体左右两侧的两点(灭点),所以叫两点透视
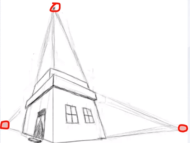
3>、三点透视
一般常见于物体的俯视和仰视,物体各个边的延长线会分别消失于三个点。
两点透视是最常用的透视关系,其次是一点透视,而三点透视只适合表现高大物体,并不常用
三、
1、生成透视投影图的方法
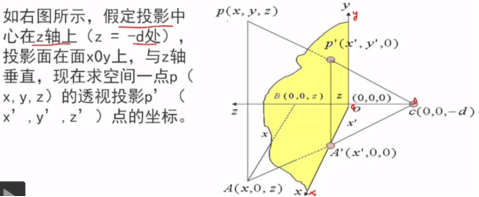
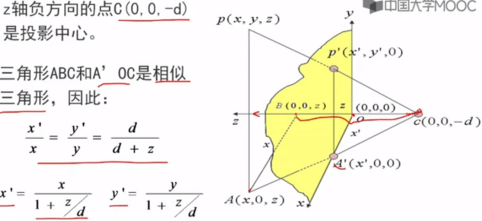
(1)透视坐标与z值成反比,即z值越大,透视坐标值越小
(2)D的取值不同,可以对形成的透视图有放大和缩小的功能。当d值较大时,形成的透视图越大,反之缩小。

第一个矩阵为透视变换矩阵,第二个矩阵为在x0y面上投影

