直线裁剪算法
一、
1、裁剪:确定图形哪些部分落在显示区之内,哪些落在显示区外。这个选择的过程就称为裁剪。
2、直线段的裁剪:Cohen-Suther land、中点分割法和Liang-Barsky裁剪算法
二、Cohen-Suther land算法
又称编码裁剪算法,算法的基本思想是对每条直线分三种情况处理:
1>若端点完全在裁剪窗口内----“简取”之
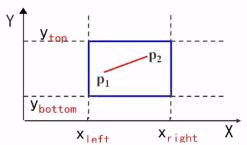
2>若端点完全在裁剪窗口外,且满足下列四个条件之一----“简弃”之
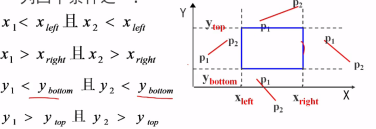
3>既不满足简取,也不满足简弃:对直线段按交点进行分段,分段后判断直线是“简取”还是“简弃”
每条线段的端点都赋以四位二进制码D3D2D1D0,编码规则如下:(左右下上)

例如:
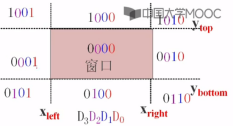
裁剪一条线段时,先求出端点P1,P2的编码code,然后进行二进制“或”和“与”运算
(1)若code1|code2=0,对直线段简取
(2)若code1&code2不等于0,对直线段简弃
(3)若上述两条件都不成立,则需要求出直线段与窗口边界的交点,并在交点处把直线段一分为二
3、存在问题:
一条完全在窗口外的直线,进行与运算=0,还需求交点,然后所得结果还是全部舍弃三、
三、中点分割算法
1、核心思想:通过二分逼近来确定直线段与窗口的交点
2、注意:
1>若中点不在窗口内,则把中点和离窗口边界最远点构成的线段丢掉,线段上的另一点和该中点再构成线段求其中点
2>若中点在窗口内,则以中点和最远点构成线段,求其中点,直到中点与窗口边界的坐标值在规定的误差范围内
3、问题:中点分割算法会不会无限循环下去?
不会。因为屏幕像素是有限的,一般计算次数不会太多,而且允许在误差范围内
四、Liang-Barsky裁剪算法
1、主要思想:用参数方程表示一条直线段(0<=U<=1)
X=X1+U*(X2-X1)=X1+U*△X
Y=Y1+U*(Y2-Y1)=Y1+U*△Y
2、把直线看成是一条有方向的线段,把窗口的四条边及其延长线分成两类:入边和出边
入边:左边界和下边界
出边:右边界和上边界
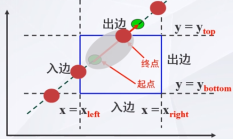
如何求出起点和终点的坐标?(即起点和终点的参数值u)
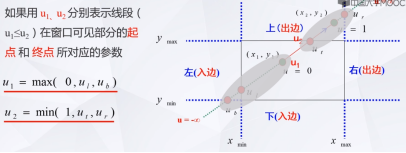
判断线段某一部分是否在窗口内,可以简化为判断直线上一个点是否在窗口内的问题,窗口内的P点满足什么条件?
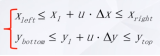
3、举例:
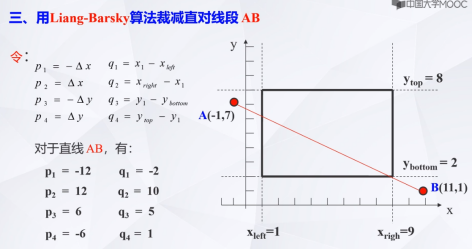


3、Liang-Barsky算法小结
1>直线方程参数化
2>直线段是有方向的
3>把窗口的四条边分成入边和出边
五、Cohen-Suther land算法和Liang-Barsky算法比较
1、Cohen-Suther land算法的核心思想是编码,窗口和延长线把空间分成了9个区域
2、线段要么大部分在窗口外,要么大部分在窗口内,使用Cohen-Suther land效果好
3、一般情况下(线段贯穿窗口),优先使用Liang-Barsky算法
4、两者均只能应用于矩形窗口

