线性规划解网络流的例子

1.某公司要用铁路运送2种物品，分别从城市s1、s2到d1、d2，每个物品每天要送出0.5单位。给出城市之间每天铁路的流量限制。假设物品可以任意地分成若干份，从而可以分别从不同的线路走。求一个开销最小的运送方案。如图：（ef之间出了故障。）

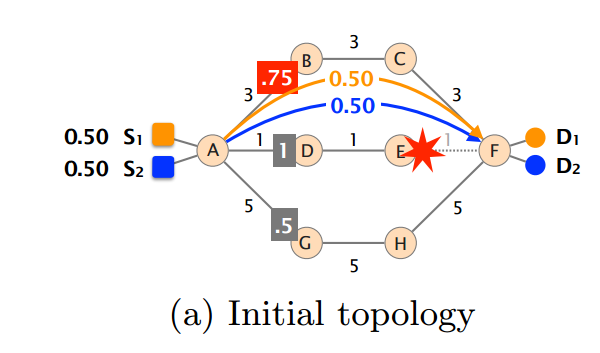
2个流s1--d1(设为流1)和s2--d2(设为流2)，均只有3条路可以走：a-b-c-f(设为路径1)，a-d-e-f(设为路径2)，a-g-h-f(设为路径3)。设2个流在3条路径上的流量分别为：x11,x12,x13,x21,x22,x23。

则目标函数：

min (9x11+9x21+10000x12+10000x22+15x13+15x23)

这里因为df断了，故令路径2的开销为10000，代表正无穷。

约束条件：

x11+x12+x13=0.5
x21+x22+x23=0.5
x11+x21<=0.75
x12+x22<=1
x13+x23<=0.5

 

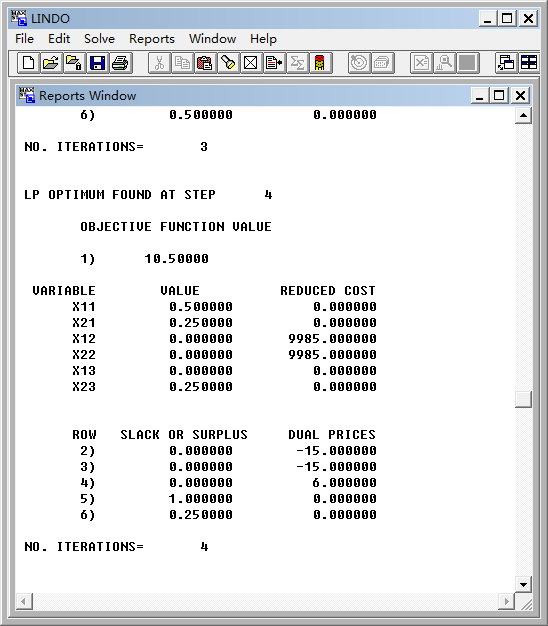
解得x11=0.5，x21=x23=0.25，x12=x22=x13=0

 

 

LINDO求解如图：

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

《线性规划的简单应用和实现》这篇论文中描述的线性规划解网络流的约束条件：

 

 

其中4个条件可以分别理解为：
1.每条边上的流量不能超过该边的容量
2.除源点和汇点外的其他点，流入每点的流量和从该点流出的流量相等
3.从源点发出的某个流的量，以及流入汇点的某个流的量，等于该流需求发出的量
4.每条边上的流是非负的

-----------------------------------------------------------------------------------------------------------------------------------------------

2.某公司要用铁路运送3种物品，分别从城市s1、s2、s3到d1、d2、d3，每个物品每天分别要送出0.75、0.5、0.75单位。给出城市之间每天铁路的流量限制。假设物品可以任意地分成若干份，从而可以分别从不同的线路走。求一个开销最小的运送方案。如图：

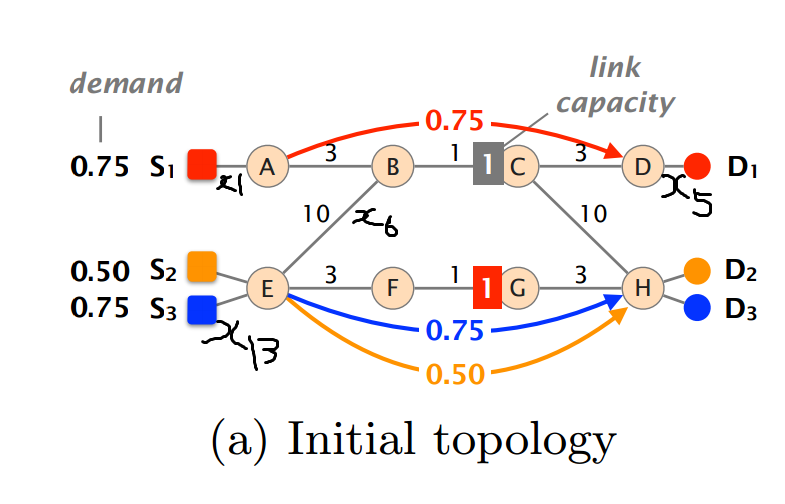
将14条边上的3种流分别设为x11，x12，……，x114，x21，x22，……，x214，x31，x32，……，x314如图，依次类推。

则目标函数为：

min （3x12+3x22+3x32+x13+x23+x33+3x14+3x24+3x34+10x16+10x26+10x36+10x17+10x27+10x37+3x19+3x29+3x39+x110+x210+x310+3x111+3x211+3x311）

约束条件为：

x13+x23+x33<=1
x110+x210+x310<=1
x11=0.75
x21=0
x31=0
x18=0
x28=0.5
x38=0
x113=0
x213=0
x313=0.75
x15=0.75
x25=0
x35=0
x112=0
x212=0.5
x312=0
x114=0
x214=0
x314=0.75
x11-x12=0
x21-x22=0
x31-x32=0
x12+x16-x13=0
x22+x26-x23=0
x32+x36-x33=0
x13-x14-x17=0
x23-x24-x27=0
x33-x34-x37=0
x14-x15=0
x24-x25=0
x34-x35=0
x18+x113-x16-x19=0
x28+x213-x26-x29=0
x38+x313-x36-x39=0
x19-x110=0
x29-x210=0
x39-x310=0
x110-x111=0
x210-x211=0
x310-x311=0
x111+x17-x112-x114=0
x211+x27-x212-x214=0
x311+x37-x312-x314=0

 

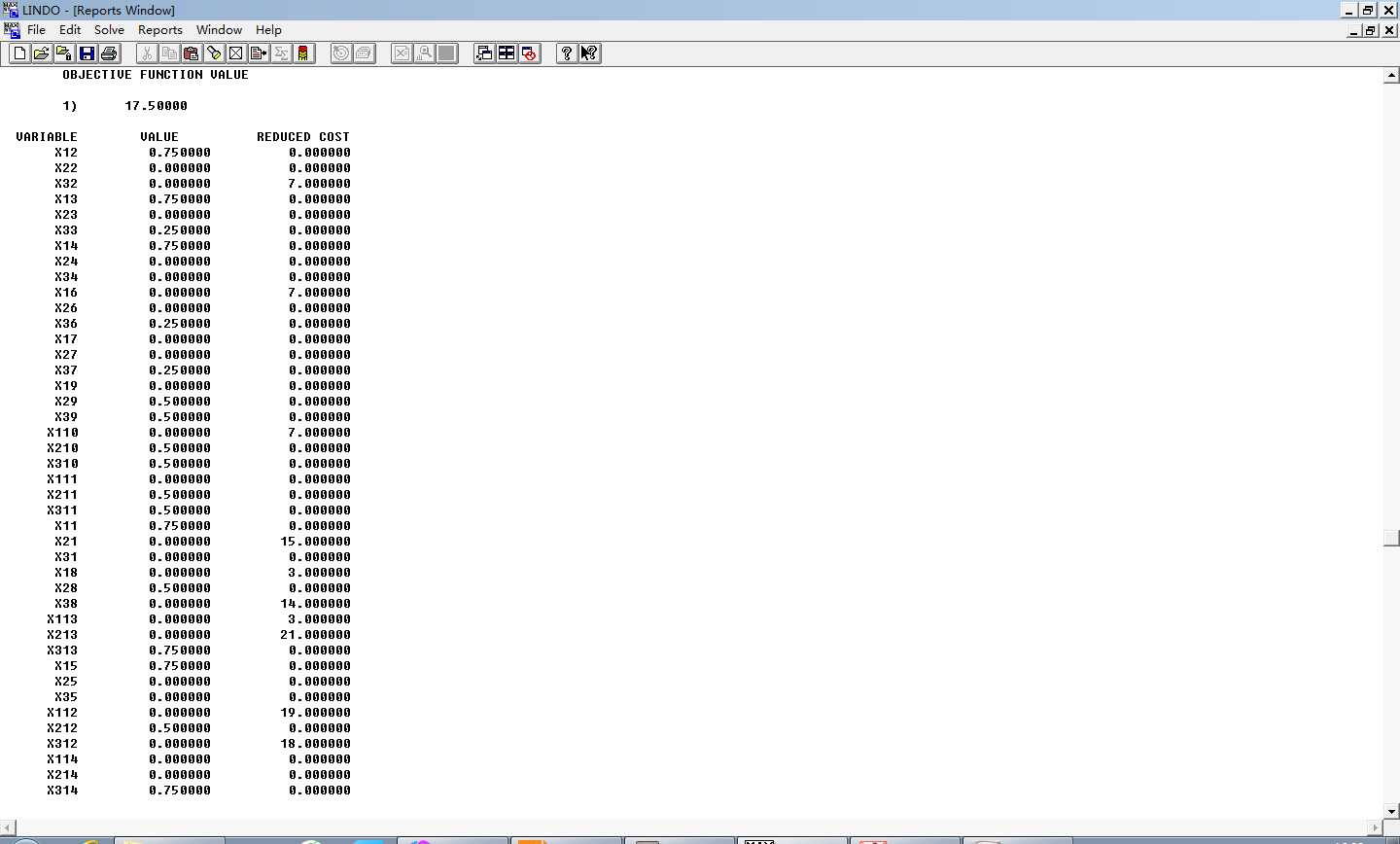
LINDO求解如图：

 

----------------------------------------------------------------------------------------------------------------------------

3.需求：流从结点c传输到红色结点，边上没有容量限制，求最小开销的路径。

如图：

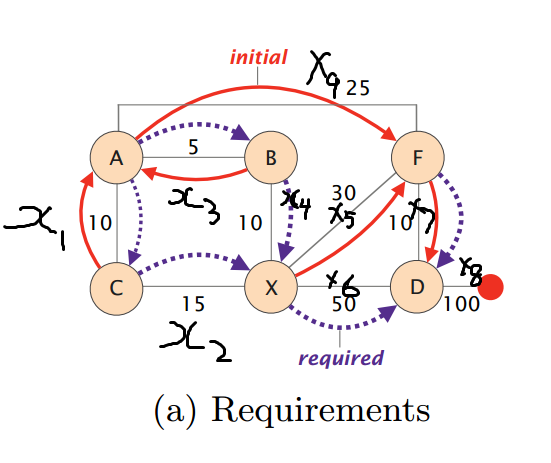
该图为无向图，将它转化为有向图，每条边转化为两条反向的边，如x1转化为x11和x21，x2转化为x12和x22……

目标函数：

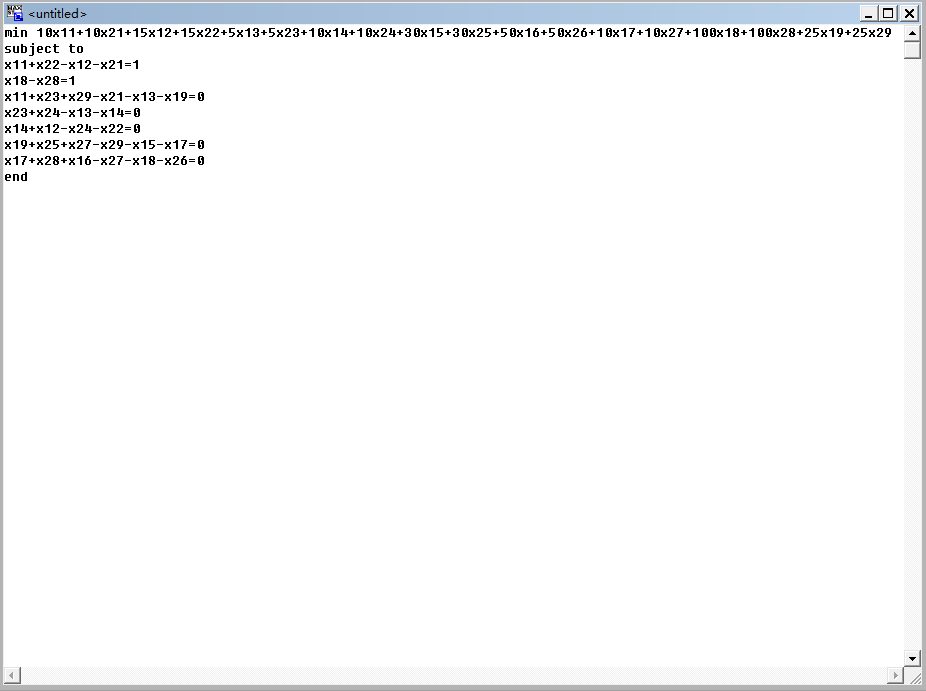
min 10x11+10x21+15x12+15x22+5x13+5x23+10x14+10x24+30x15+30x25+50x16+50x26+10x17+10x27+100x18+100x28+25x19+25x29

约束条件：

x11+x22-x12-x21=1
x18-x28=1
x11+x23+x29-x21-x13-x19=0
x23+x24-x13-x14=0
x14+x12-x24-x22=0
x19+x25+x27-x29-x15-x17=0
x17+x28+x16-x27-x18-x26=0

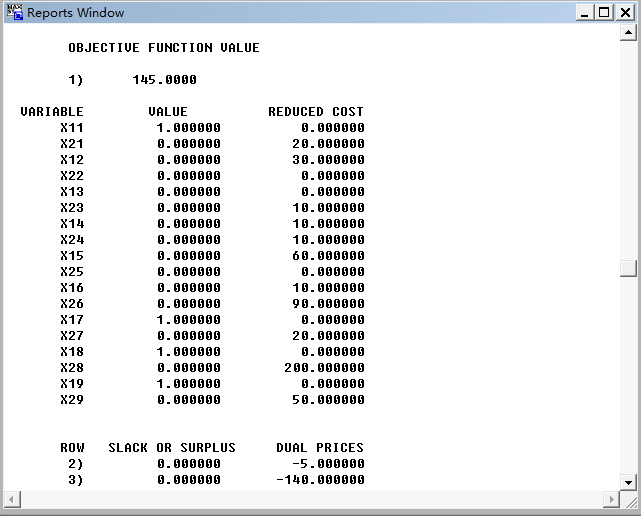
得出CAFD的路径。

LINDO求解如图：

----------------------------------------------------------------------------------------------------------------

4.若上图要求从B传到红色结点。

目标函数不变，约束条件变为：

x11+x22-x12-x21=0
x18-x28=1
x11+x23+x29-x21-x13-x19=0
x23+x24-x13-x14=1
x14+x12-x24-x22=0
x19+x25+x27-x29-x15-x17=0
x17+x28+x16-x27-x18-x26=0

LINDO解出BAFD的路径。