Chapter 5 - Outlier Analysis
Segment 8 - Extreme value analysis using univariate methods
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import rcParams
%matplotlib inline
rcParams['figure.figsize'] = 5,4
address = '~/Data/iris.data.csv'
df = pd.read_csv(filepath_or_buffer=address, header=None, sep=',')
df.columns=['Sepal Length','Sepal Width','Petal Length','Petal Width', 'Species']
X = df.iloc[:,0:4].values
y = df.iloc[:,4].values
df[:5]
|
Sepal Length |
Sepal Width |
Petal Length |
Petal Width |
Species |
| 0 |
5.1 |
3.5 |
1.4 |
0.2 |
setosa |
| 1 |
4.9 |
3.0 |
1.4 |
0.2 |
setosa |
| 2 |
4.7 |
3.2 |
1.3 |
0.2 |
setosa |
| 3 |
4.6 |
3.1 |
1.5 |
0.2 |
setosa |
| 4 |
5.0 |
3.6 |
1.4 |
0.2 |
setosa |
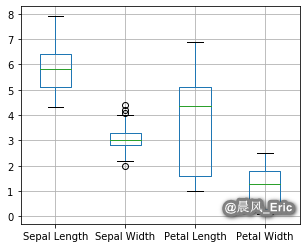
Identifying outliers from Tukey boxplots
df.boxplot(return_type='dict')
plt.plot()
[]
Sepal_Width = X[:,1]
iris_outliers = (Sepal_Width > 4)
df[iris_outliers]
|
Sepal Length |
Sepal Width |
Petal Length |
Petal Width |
Species |
| 15 |
5.7 |
4.4 |
1.5 |
0.4 |
setosa |
| 32 |
5.2 |
4.1 |
1.5 |
0.1 |
setosa |
| 33 |
5.5 |
4.2 |
1.4 |
0.2 |
setosa |
Sepal_Width = X[:,1]
iris_outliers = (Sepal_Width < 2.05)
df[iris_outliers]
|
Sepal Length |
Sepal Width |
Petal Length |
Petal Width |
Species |
| 60 |
5.0 |
2.0 |
3.5 |
1.0 |
versicolor |
Applying Tukey outlier labeling
pd.options.display.float_format = '{:.1f}'.format
X_df = pd.DataFrame(X)
print(X_df.describe())
0 1 2 3
count 150.0 150.0 150.0 150.0
mean 5.8 3.1 3.8 1.2
std 0.8 0.4 1.8 0.8
min 4.3 2.0 1.0 0.1
25% 5.1 2.8 1.6 0.3
50% 5.8 3.0 4.3 1.3
75% 6.4 3.3 5.1 1.8
max 7.9 4.4 6.9 2.5
