线性回归R实例
一、一元线性回归
以R中自带的trees数据集为例进【微软visual studio2017中R相关数据科学模块】
> head(trees) Girth Height Volume#包含树龄、树高、体积 1 8.3 70 10.3 2 8.6 65 10.3 3 8.8 63 10.2 4 10.5 72 16.4 5 10.7 81 18.8 6 10.8 83 19.7
先绘制一下散点图,看看变量之间是否存在线性关系:体积、树龄
> library(ggplot2) > qplot(x = log(Girth),y = log(Volume),data = trees,main = 'Volume and Girth Relation', colour = I('skyblue'),size = 10)

有图得知,存在线性关系,进行建模
> model<-lm(Volume~Girth,data = trees) > summary(model) Call: lm(formula = Volume ~ Girth, data = trees) Residuals:#残差较大 Min 1Q Median 3Q Max -8.065 -3.107 0.152 3.495 9.587 Coefficients:#系数的假设检验,P值都较小,在模型中呈显著状态*** Estimate Std. Error t value Pr(>|t|) (Intercept) -36.9435 3.3651 -10.98 7.62e-12 *** Girth 5.0659 0.2474 20.48 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 4.252 on 29 degrees of freedom Multiple R-squared: 0.9353, Adjusted R-squared: 0.9331 F-statistic: 419.4 on 1 and 29 DF, p-value: < 2.2e-16 #F统计量,也是显著的
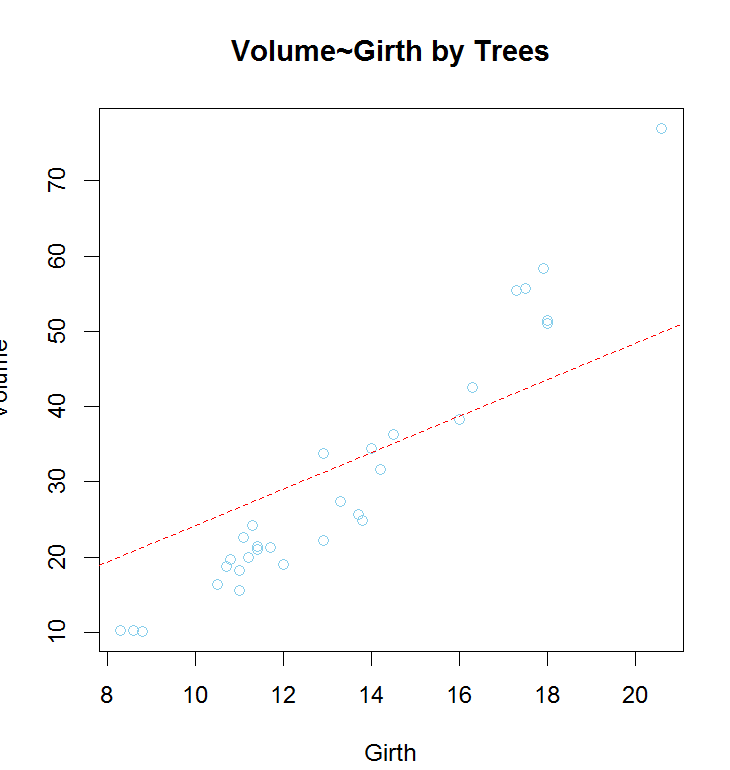
将拟合直线绘制到原图上,查看拟合情况
> plot(Volume ~ Girth, data = trees,main = 'Volume and Girth Relation', col = 'skyblue') + abline(model, col = 'red', lty = 3)

但截距项不应该为负数(无论树龄再小体积也不应该为负数,就算只是一颗种子它也是有体积的),所以也可以用下面方法将截距强制为0:
> model <- lm(Volume ~ Girth - 1, data = trees) + summary(model) Call: lm(formula = Volume ~ Girth - 1, data = trees) Residuals:#残差有所增大 Min 1Q Median 3Q Max -11.104 -8.470 -6.199 1.883 27.129 Coefficients: Estimate Std. Error t value Pr(>|t|) Girth 2.4209 0.1253 19.32 <2e-16 *** #截距项已经去除只剩树龄 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.493 on 30 degrees of freedom Multiple R-squared: 0.9256, Adjusted R-squared: 0.9231 F-statistic: 373.1 on 1 and 30 DF, p-value: < 2.2e-16
将现在的模型与之前的模型进行比较
也可以plot模型输出结果,评价模型效果
par(mfrow=c(2,2)) plot(model)

左上图是残差对拟合值作图,整体呈现出一种先下降后下升的模式,显示残差中可能还存在未提炼出来的影响因素。
右上图残差QQ图,用以观察残差是否符合正态分布。
左下图是标准化残差对拟合值,用于判断模型残差是否等方差。
右下图是标准化残差对杠杆值,虚线表示的cooks距离等高线。我们发现31号样本有较大的影响,需要进行变换。
plot(sqrt(Volume)~Girth,data=trees,pch=16,col='skyblue')#对整体进行开根号变换,线性趋势仍然明显

plot(log(Volume) ~ Girth, data = trees, pch = 16, col = 'red')#对整体进行log变换,

与开根号趋势差异不大,采用开根号后变换重新进行建模
> model <- lm(sqrt(Volume) ~ Girth, data = trees) + summary(model) Call: lm(formula = sqrt(Volume) ~ Girth, data = trees) Residuals:#整体残差明显变小 Min 1Q Median 3Q Max -0.56640 -0.19429 -0.01169 0.20934 0.65575 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.55183 0.23719 -2.327 0.0272 * Girth 0.44262 0.01744 25.385 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.2997 on 29 degrees of freedom Multiple R-squared: 0.9569, Adjusted R-squared: 0.9555 F-statistic: 644.4 on 1 and 29 DF, p-value: < 2.2e-16
> plot(sqrt(Volume) ~ Girth, data = trees, pch = 16, col = 'red') + abline(model, lty = 2)

其实跟最初拟合的效果差别不大
par(mfrow=c(2,2)) plot(model)

上图可知,原先的31号点已被削减,基本上没有太明显的异常点
预测使用时只需要输入建立模型名称以及数据框(包含X属性的列名,本列中即树龄),预测值为体积
> head(predict(model, trees)) 1 2 3 4 5 6 3.121955 3.254743 3.343268 4.095729 4.184254 4.228516
二、多元线性回归
与一元线性回归不同的是采用多个自变量来预测或者估计因变量
步骤与一元类似:
1、相关性检验,共线变量需要进行一定取舍,可以通过corrplot(cor(数据框名称))查看相关性
2、model <- lm(因变量~自变量1+自变量2+自变量3..., data = 数据框名称)进行建模,summary进行查看模型效果
3、同样可以用par(mfrow=c(2,2))、plot(model)查看效果及异常点情况
4、根据结果进行调整,重新建模,直到获得较为满意的结果为止。
三、广义线性回归
基本语法
逻辑回归,再根据结果进行
model <- glm(因变量~自变量1 +自变量2 + 自变量3..., data = 数据框, family = binomial)
泊松回归:修改family
老师原文地址:https://notebooks.azure.com/YukWang/libraries/rDataAnalysis




 浙公网安备 33010602011771号
浙公网安备 33010602011771号