2021.9.25考试总结[NOIP模拟61]
终于有点阳间题了然而挂了60pts
哈哈
T1 交通
类似简单题,限制看似很复杂,但不难发现当确定一条边是否被删后会产生裙带关系,很多边会跟着自动被确定是否被删。
仔细观察可以得出这种关系会构成偶环结构,于是记录每条边是源点的第几条出边,汇点的第几条入边,类似链表,找出这些环即可。最后答案为\(2^{环数}\)。
注意边数是点数二倍,数组开够。血的教训
\(code:\)
T1
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace IO{
inline int read(){
char ch=getchar(); int x=0,f=1;
while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
return x*f;
}
inline void write(int x,char sp){
char ch[20]; int len=0;
if(x<0){ putchar('-'); x=~x+1; }
do{ ch[len++]=(1<<4)+(1<<5)+x%10; x/=10; }while(x);
for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
}
inline int max(int x,int y){ return x<y?y:x; }
inline int min(int x,int y){ return x<y?x:y; }
inline void swap(int& x,int& y){ x^=y^=x^=y; }
inline void ckmax(int& x,int y){ x=x<y?y:x; }
inline void ckmin(int& x,int y){ x=x<y?x:y; }
} using namespace IO;
const int NN=1e5+5,p=998244353;
int n,tot,u[NN<<1],v[NN<<1],in[NN][2],ot[NN][2];
bool is[NN<<1],pos[NN<<1][2];
inline int qpow(int a,int b){
int res=1;
while(b){
if(b&1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
void solve(int i){
bool type=0;
int now=i;
do{
is[now]=1;
if(!type) now=in[v[now]][pos[now][0]^1];
else now=ot[u[now]][pos[now][1]^1];
type^=1;
}while(!is[now]);
}
signed main(){
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
n=read();
for(int i=1;i<=n*2;i++){
u[i]=read(),v[i]=read();
if(!in[v[i]][0]) in[v[i]][0]=i, pos[i][0]=0;
else in[v[i]][1]=i, pos[i][0]=1;
if(!ot[u[i]][0]) ot[u[i]][0]=i, pos[i][1]=0;
else ot[u[i]][1]=i, pos[i][1]=1;
}
for(int i=1;i<=n*2;i++) if(!is[i]){
++tot;
solve(i);
}
write(qpow(2,tot),'\n');
return 0;
}
T2 小P的单调数列
记\(f_{i,j}\)为考虑到第\(i\)个位置,第\(j\)个区间的子序列最大和。有:
\(f_{i,j}=\begin{cases}max(0,max_{k<i \wedge a_k<a_i} \left \{ f_{k,1} \right \}) & \text{ if } \textrm{j=1} \\ max(max_{k<i \wedge a_k<a_i}\left \{ f_{k,j} \right \},max_{k<i \wedge a_k\leq a_i}\left \{ f_{k,j-1} \right \}) & \text{ if } \textrm{j>1}\wedge\textrm{(j mod 2=1)} \\ max(max_{k<i \wedge a_k>a_i}\left \{ f_{k,j} \right \},max_{k<i \wedge a_k \geq a_i\left \{ f_{k,j-1} \right \}}) & \text{ if } \textrm{(j mod 2=0)} \end{cases}\)
很显然可以线段树优化。
发现许多区间的平均值一定不大于其中某个区间的值,所以递增与递减的区间都至多有一个,因此无需枚举\(j\)。
\(code:\)
T2
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long double DB;
namespace IO{
inline int read(){
char ch=getchar(); int x=0,f=1;
while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
return x*f;
}
inline void write(int x,char sp){
char ch[20]; int len=0;
if(x<0){ putchar('-'); x=~x+1; }
do{ ch[len++]=(1<<4)+(1<<5)+x%10; x/=10; }while(x);
for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
}
inline LL max(LL x,LL y){ return x<y?y:x; }
inline int min(int x,int y){ return x<y?x:y; }
inline void swap(int& x,int& y){ x^=y^=x^=y; }
inline void ckmax(LL& x,LL y){ x=x<y?y:x; }
inline void ckmin(int& x,int y){ x=x<y?x:y; }
} using namespace IO;
const int NN=100010;
const DB eps=1e-8;
int n,a[NN];
int ext,has[NN];
LL tmp;
DB ans;
void init(){
for(int i=1;i<=n;i++) has[i]=a[i];
sort(has+1,has+n+1);
ext=unique(has+1,has+n+1)-has-1;
for(int i=1;i<=n;i++)
a[i]=lower_bound(has+1,has+ext+1,a[i])-has;
}
struct segment_tree{
#define ld rt<<1
#define rd (rt<<1)|1
LL mx[NN<<2];
void pushup(int rt){
mx[rt]=max(mx[ld],mx[rd]);
}
void insert(int rt,int l,int r,int pos,LL val){
if(l==r) return ckmax(mx[rt],val);
int mid=l+r>>1;
if(pos<=mid) insert(ld,l,mid,pos,val);
else insert(rd,mid+1,r,pos,val);
pushup(rt);
}
LL query(int rt,int l,int r,int opl,int opr){
if(opl>opr) return -4e18;
if(l>=opl&&r<=opr) return mx[rt];
int mid=l+r>>1;
LL res=0;
if(opl<=mid) ckmax(res,query(ld,l,mid,opl,opr));
if(opr>mid) ckmax(res,query(rd,mid+1,r,opl,opr));
return res;
}
}up,dn;
signed main(){
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)
a[i]=read();
init();
memset(up.mx,0xc0,sizeof(up.mx));
memset(dn.mx,0xc0,sizeof(dn.mx));
for(int i=1;i<=n;i++){
tmp=max(dn.query(1,1,n,a[i]+1,n),up.query(1,1,n,a[i],n))+has[a[i]];
if(1.0*tmp/2-ans>eps) ans=1.0*tmp/2;
if(tmp>0) dn.insert(1,1,n,a[i],tmp);
tmp=up.query(1,1,n,1,a[i]-1)+has[a[i]];
if(1.0*tmp-ans>eps) ans=1.0*tmp;
if(tmp>0) up.insert(1,1,n,a[i],tmp);
}
printf("%.3Lf\n",ans+eps);
return 0;
}
T3 矩阵
神仙题。
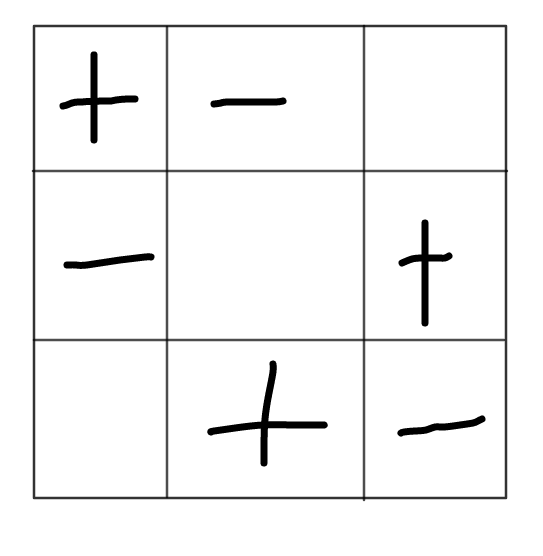
考虑上图,任何\(3\times3\)的矩阵中三个加号位置的和减三个三个减号位置的和总是不变的,因为任意行列与主对角线上都有一加一减。拓展一下,发现如果有解,其实只要将左上两行两列消完即可。
判断有解可以枚举所有\(3\times3\)的矩形,有解当且仅当所有矩形上面所述的值为\(0\)。
消左上行列,可以先把左上角\(2\times2\)消成\(0\),然后用主对角线把上两行竖着相邻的格子两两弄得相等,左两列横着相邻的格子两两弄得相等,最后直接消掉。
\(code:\)
T3
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace IO{
inline int read(){
char ch=getchar(); int x=0,f=1;
while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
return x*f;
}
inline void write(int x,char sp){
char ch[20]; int len=0;
if(x<0){ putchar('-'); x=~x+1; }
do{ ch[len++]=(1<<4)+(1<<5)+x%10; x/=10; }while(x);
for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
}
inline int max(int x,int y){ return x<y?y:x; }
inline int min(int x,int y){ return x<y?x:y; }
inline void swap(int& x,int& y){ x^=y^=x^=y; }
inline void ckmax(int& x,int y){ x=x<y?y:x; }
inline void ckmin(int& x,int y){ x=x<y?x:y; }
} using namespace IO;
const int NN=1010;
int n,m,a[NN][NN];
int num,ans[6010][3];
void print(int id){
write(ans[id][0],' ');
write(ans[id][1],' ');
write(ans[id][2],'\n');
}
signed main(){
freopen("c.in","r",stdin);
freopen("c.out","w",stdout);
n=read(); m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
a[i][j]=read();
if(n==1){
cout<<m<<endl;
for(int i=1;i<=m;i++)
cout<<2<<' '<<i<<' '<<-a[1][i]<<endl;
return 0;
}
if(m==1){
cout<<n<<endl;
for(int i=1;i<=n;i++)
cout<<1<<' '<<i<<' '<<-a[i][1]<<endl;
return 0;
}
for(int i=1;i<n-1;i++)
for(int j=1;j<m-1;j++)
if(a[i][j]-a[i+1][j]-a[i][j+1]+a[i+1][j+2]+a[i+2][j+1]-a[i+2][j+2]!=0)
puts("-1"), exit(0);
ans[++num][0]=1; ans[num][1]=1; ans[num][2]=-a[1][1];
for(int i=m;i;i--) if(i!=1) a[1][i]-=a[1][1]; a[1][1]=0;
ans[++num][0]=1; ans[num][1]=2; ans[num][2]=-a[2][2];
for(int i=m;i;i--) if(i!=2) a[2][i]-=a[2][2]; a[2][2]=0;
ans[++num][0]=3; ans[num][1]= 1; ans[num][2]=-a[1][2]; a[2][3]-=a[1][2]; a[1][2]=0;
ans[++num][0]=3; ans[num][1]=-1; ans[num][2]=-a[2][1]; a[3][2]-=a[2][1]; a[2][1]=0;
for(int i=3;i<=m;i++){
ans[++num][0]=3; ans[num][1]=i-1; ans[num][2]=a[2][i]-a[1][i]; a[2][i+1]+=ans[num][2];
ans[++num][0]=2; ans[num][1]=i; ans[num][2]=-a[2][i];
}
for(int i=3;i<=n;i++){
ans[++num][0]=3; ans[num][1]=1-i; ans[num][2]=a[i][2]-a[i][1]; a[i+1][2]+=ans[num][2];
ans[++num][0]=1; ans[num][1]=i; ans[num][2]=-a[i][2];
}
write(num,'\n');
for(int i=1;i<=num;i++)
print(i);
return 0;
}
T4 花瓶

T4
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace IO{
inline int read(){
char ch=getchar(); int x=0,f=1;
while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
return x*f;
}
inline void write(int x,char sp){
char ch[20]; int len=0;
if(x<0){ putchar('-'); x=~x+1; }
do{ ch[len++]=(1<<4)+(1<<5)+x%10; x/=10; }while(x);
for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
}
inline int max(int x,int y){ return x<y?y:x; }
inline int min(int x,int y){ return x<y?x:y; }
inline void swap(int& x,int& y){ x^=y^=x^=y; }
inline void ckmax(int& x,int y){ x=x<y?y:x; }
inline void ckmin(int& x,int y){ x=x<y?x:y; }
} using namespace IO;
const int NN=5010;
int n,ans,a[NN],id[NN],sum[NN],f[NN][NN];
int stk[NN],top;
bool cmp(int a,int b){ return sum[a]<sum[b]; }
signed main(){
freopen("d.in","r",stdin);
freopen("d.out","w",stdout);
n=read();
memset(f,0xc0,sizeof(f)); ans=0;
for(int i=0;i<=n;i++) f[i][0]=0;
for(int i=1;i<=n;i++){
a[i]=read(); id[i]=i;
sum[i]=sum[i-1]+a[i];
}
sort(id,id+n+1,cmp);
for(int j=1;j<=n;j++){
top=0;
for(int x,i=0;i<=n;i++){
x=id[i];
if(x>=j) continue;
while(top>1&&(f[j][stk[top-1]]-f[j][stk[top]])*(sum[stk[top]]-sum[x])<=
(f[j][stk[top]]-f[j][x])*(sum[stk[top-1]]-sum[stk[top]])) --top;
stk[++top]=x;
}
for(int x,l=1,i=n;~i;i--){
x=id[i];
if(x<=j) continue;
while(l<top&&f[j][stk[l]]-f[j][stk[l+1]]<=
(sum[x]-sum[j])*(sum[stk[l]]-sum[stk[l+1]])) ++l;
int k=stk[l];
ckmax(f[x][j],f[j][k]-(sum[x]-sum[j])*sum[k]+sum[x]*sum[j]-sum[j]*sum[j]);
}
}
for(int i=0;i<n;i++) ckmax(ans,f[n][i]);
write(ans,'\n');
return 0;
}


