2021.9.7考试总结[NOIP模拟49]

T1 Reverse

---

$BFS$暴力$O(n^2)$

过程中重复枚举了很多点，考虑用链表记录当前点后面可到达的第一个未更新点。

搜索时枚举翻转子串的左端点，之后便可以算出翻转后$1$的位置。

$code:$

#include<bits/stdc++.h>
using namespace std;

namespace IO{
    inline int read(){
        char ch=getchar(); int x=0,f=1;
        while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
        while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
        return x*f;
    }
    inline void write(int x,char sp){
        char ch[20]; int len=0;
        if(x<0){ putchar('-'); x=~x+1; }
        do{ ch[len++]=x%10+(1<<4)+(1<<5); x/=10; }while(x);
        for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
    }
    inline int max(int x,int y){ return x<y?y:x; }
    inline int min(int x,int y){ return x<y?x:y; }
    inline void swap(int &x,int &y){ x^=y^=x^=y; }
    inline void chmax(int &x,int y){ x=x<y?y:x; }
    inline void chmin(int &x,int y){ x=x<y?x:y; }
} using namespace IO;

const int NN=1e5+5;
int n,m,s,k,dis[NN],nex[NN];
bool ban[NN];
vector<int>move;

void bfs(){
    memset(dis,-1,sizeof(dis));
    queue<int>q;
    for(int i=1;i<=n;i++) nex[i]=i+2;
    dis[s]=0; q.push(s);
    while(!q.empty()){
        int x=q.front(),l=max(1,x-k+1),r=min(x,n-k+1),tmp;
        for(int i=2*l+k-x-1;i<=2*r+k-x-1;i=tmp){
            tmp=nex[i]; nex[i]=nex[2*r+k-x-1];
            if(i>n||ban[i]||dis[i]>=0) continue;
            dis[i]=dis[x]+1; q.push(i);
        }
        q.pop();
    }
}

signed main(){
    n=read(); k=read(); m=read(); s=read();
    for(int i=1;i<=m;i++) ban[read()]=1;
    bfs();
    for(int i=1;i<=n;i++) write(dis[i],' ');
    return 0;
}

T2 Silhouette

---

首先每一行与每一列都有交点，所以排序不影响方案数。于是先将$a,b$排序。如果$a_{max} \neq b_{max}$则无解。

考虑从大到小枚举$a,b$的值$s$，考虑$min(a_i,b_j)=s$的情况，那么每次考虑的位置会构成一个$L$形或矩形。而矩形又可以看作特殊的$L$。

对于$s_{max}$，考虑范围是右上角的矩形。考虑容斥，设$f_i$为矩形中至少$i$行不合法的方案数，令矩形$a$行$b$列，则有

$f[i]=C_a^i\times (S^i\times ((S+1)^{a-i}-S^{a-i}))^b$。

答案即为$\sum_{i=0}^a (-1)^i \times f_i$。

再考虑普遍情况。考虑如下图形

 

 

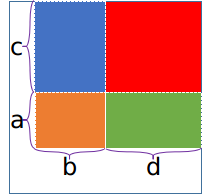
 其中红色部分已满足行列要求。因此蓝色部分不能不满足行要求，绿色部分不能不满足列要求。

可以将蓝橙绿分为蓝橙和绿两部分分别计算。蓝橙部分类似特殊情况，但只有橙部分可能不合法。此后绿部分行列要求已被橙红两块满足，随便选即可。

令$f_i$为$a$中有至少$i$行不合法，有

$f[i]=C_a^i\times (S^i\times ((S+1)^{a+c-i}-S^{a+c-i}))^b\times (S^i\times (S+1)^{a-i})^d$

一样容斥，最后累乘即可。

$code:$

#include<bits/stdc++.h>
#define int long long
using namespace std;

namespace IO{
    inline int read(){
        char ch=getchar(); int x=0,f=1;
        while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
        while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
        return x*f;
    }
    inline void write(int x,char sp){
        char ch[20]; int len=0;
        if(x<0){ putchar('-'); x=~x+1; }
        do{ ch[len++]=x%10+(1<<4)+(1<<5); x/=10; }while(x);
        for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
    }
    inline int max(int x,int y){ return x<y?y:x; }
    inline int min(int x,int y){ return x<y?x:y; }
    inline void swap(int &x,int &y){ x^=y^=x^=y; }
    inline void chmax(int &x,int y){ x=x<y?y:x; }
    inline void chmin(int &x,int y){ x=x<y?x:y; }
} using namespace IO;

const int NN=1e5+5,p=1e9+7;
int n,ans,ext,tma,tmb,pra,prb,a[NN],b[NN],s[NN<<1];

namespace math{
    int fac[NN],inv[NN];
    inline int C(int x,int y){
        if(x<y) return 0;
        return fac[x]*inv[y]%p*inv[x-y]%p;
    }
    inline int qpow(int x,int y){
        int res=1;
        while(y){
            if(y&1) res=res*x%p;
            x=x*x%p;
            y>>=1;
        }
        return res;
    }
    void init(){
        fac[0]=inv[0]=1;
        for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%p;
        inv[n]=qpow(fac[n],p-2);
        for(int i=n-1;i;i--) inv[i]=inv[i+1]*(i+1)%p;
    }
} using namespace math;

inline int calc(int mia,int mib,int upa,int upb,int num){
    int res=0;
    for(int i=0;i<=mia;i++){
        int now=C(mia,i)*qpow(qpow(num,i)*(qpow(num+1,mia+upa-i)-qpow(num,mia+upa-i)+p)%p,mib)%p;
        now=now*qpow(qpow(num,i)*qpow(num+1,mia-i)%p,upb)%p;
        if(i&1) now=p-now;
        (res+=now)%=p;
    }
    return res;
}

signed main(){
    n=read(); init(); ans=1;
    for(int i=1;i<=n;i++) s[i]  =a[i]=read();
    for(int i=1;i<=n;i++) s[i+n]=b[i]=read();
    sort(a+1,a+n+1); sort(b+1,b+n+1); sort(s+1,s+2*n+1);
    ext=unique(s+1,s+2*n+1)-s-1;
    if(a[n]!=b[n]){ puts("0"); return 0; }
    pra=prb=n+1; tma=tmb=n;
    for(int i=ext;i;i--){
        while(a[tma-1]==s[i]&&tma-1) --tma;
        while(b[tmb-1]==s[i]&&tmb-1) --tmb;
        (ans*=calc(pra-tma,prb-tmb,n-pra+1,n-prb+1,s[i]))%=p;
        pra=tma; prb=tmb;
    }
    write(ans,'\n');
    return 0;
}

T3 Seat

---

skyh倾情压行注释（？

发现每次选座位区间长度的可重集是固定的，可以按照最大距离分层，然后进行$DP$。分奇偶讨论，

 

多理解几节课就差不多了..

不放代码了（几乎一样还放个锤子