[BZOI2014]大融合——————线段树进阶
竟然改了不到一小时就改出来了, 可喜可贺
Description
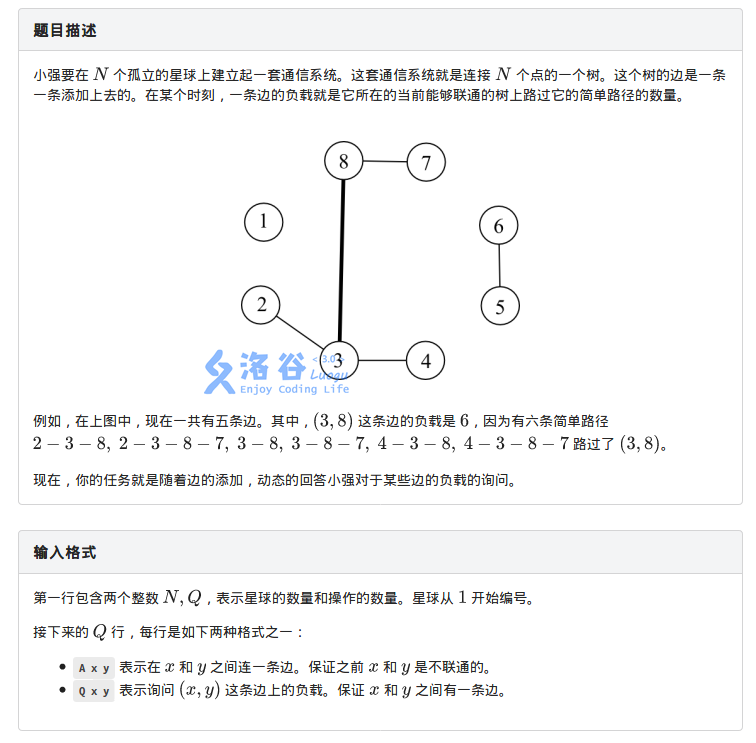
Solution
一开始想的是边两侧简单路径之和的乘积,之后发现这是个树形结构,简单路径数就是节点数。
之后的难点就变成了如何求线段树中不连续且无序区间中的权值。答案当然是没办法求
所以我们要进行离线,现将所有建边信息记录下来,把最终形成的树建好,然后在树上求DFS序。这样就能保证一个子树内的节点编号是连续的。
在查询时给出的两点一定具有父子关系,只需先找出二者中的儿子,之后求出它们所在树的节点树与儿子子树的节点树,做差后相乘即可。
CODE:

1 #include<bits/stdc++.h> 2 #define debug cout<<"lbwnb" 3 using namespace std; 4 const int NN=1e5+10; 5 int siz[NN],dep[NN],lin[NN],tmp,to[NN*2],n,q,rt[NN],x,y,fa[NN],dat[NN][3],nex[NN*2],head[NN],num; 6 char op[NN]; 7 inline void add(int a,int b){ 8 to[++num]=b; nex[num]=head[a]; head[a]=num; 9 to[++num]=a; nex[num]=head[b]; head[b]=num; 10 } 11 inline int getf(int x){ 12 return fa[x]==x?x:fa[x]=getf(fa[x]); 13 } 14 inline int read(){ 15 int x=0,f=1; 16 char ch=getchar(); 17 while(ch<'0'||ch>'9'){ 18 if(ch=='-') f=-1; 19 ch=getchar(); 20 } 21 while(ch>='0'&&ch<='9'){ 22 x=(x<<1)+(x<<3)+(ch^48); 23 ch=getchar(); 24 } 25 return x*f; 26 } 27 void write(int x){ 28 if(x<0) putchar('-'), x=-x; 29 if(x>9) write(x/10); 30 putchar(x%10+'0'); 31 } 32 void dfs(int x){ 33 lin[x]=++tmp; siz[x]=1; 34 for(int i=head[x];i;i=nex[i]){ 35 int v=to[i]; 36 if(dep[v]) continue; 37 dep[v]=dep[x]+1; 38 dfs(v); 39 siz[x]+=siz[v]; 40 } 41 } 42 struct node{ 43 int ls[NN*40],rs[NN*40],seg,sum[NN*40]; 44 void pushup(int x){ 45 sum[x]=sum[ls[x]]+sum[rs[x]]; 46 } 47 void insert(int &x,int l,int r,int pos,int val){ 48 if(!x) x=++seg; 49 if(l==r){ sum[x]+=val; return; } 50 int mid=(l+r)>>1; 51 if(pos<=mid) insert(ls[x],l,mid,pos,val); 52 else insert(rs[x],mid+1,r,pos,val); 53 pushup(x); 54 } 55 void merge(int &x,int y,int l,int r){ 56 if(!x||!y){ x=x+y; return; } 57 if(l==r){ sum[x]+=sum[y]; return; } 58 int mid=(l+r)>>1; 59 merge(ls[x],ls[y],l,mid); 60 merge(rs[x],rs[y],mid+1,r); 61 pushup(x); 62 } 63 int query(int x,int l,int r,int opl,int opr){ 64 if(l>=opl&&r<=opr) return sum[x]; 65 int mid=(l+r)>>1,ret=0; 66 if(opl<=mid) ret+=query(ls[x],l,mid,opl,opr); 67 if(opr>mid) ret+=query(rs[x],mid+1,r,opl,opr); 68 return ret; 69 } 70 }segt; 71 int main(){ 72 n=read(); q=read(); 73 for(int i=1;i<=q;i++) 74 cin>>op[i]>>dat[i][1]>>dat[i][2]; 75 for(int i=1;i<=q;i++) 76 if(op[i]=='A') add(dat[i][1],dat[i][2]); 77 for(int i=1;i<=n;i++) 78 if(!dep[i]) dep[i]=1,dfs(i); 79 for(int i=1;i<=n;i++) 80 segt.insert(rt[i],1,n,lin[i],1), fa[i]=i; 81 for(int i=1;i<=q;i++){ 82 if(op[i]=='A'){ 83 int r1=getf(dat[i][1]), r2=getf(dat[i][2]); 84 segt.merge(rt[r1],rt[r2],1,n); 85 fa[r2]=r1; 86 } 87 if(op[i]=='Q'){ 88 int son=dep[dat[i][1]]>dep[dat[i][2]]?dat[i][1]:dat[i][2]; 89 int ro=getf(dat[i][1]); 90 int tot=segt.query(rt[ro],1,n,1,n),sot=segt.query(rt[ro],1,n,lin[son],lin[son]+siz[son]-1); 91 write((tot-sot)*sot); putchar('\n'); 92 } 93 } 94 return 0; 95 }



