POJ 3070 Fibonacci（矩阵乘法logN）

题意：

求第n个斐波那契数，结果mod10000.

思路：

 

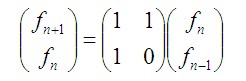
矩阵的n次方可以由二分法来解决，于是把时间缩短到了logN

#include <cstdio>
#include <cstdlib>
#include <cstring>

const int M = 10000;

typedef struct _Matrix {
    int v[2][2];
} Matrix;

Matrix m;

Matrix matrix_mul(Matrix a, Matrix b)
{
    Matrix c;
    c.v[0][0] = (a.v[0][0] * b.v[0][0] + a.v[0][1] * b.v[1][0]) % M;
    c.v[0][1] = (a.v[0][0] * b.v[0][1] + a.v[0][1] * b.v[1][1]) % M;
    c.v[1][0] = (a.v[1][0] * b.v[0][0] + a.v[1][1] * b.v[1][0]) % M;
    c.v[1][1] = (a.v[1][0] * b.v[0][1] + a.v[1][1] * b.v[1][1]) % M;
    return c;
}

Matrix matrix_pow(Matrix b, int n)
{
    if (n == 1)
        return b;
    Matrix c = matrix_pow(b, n >> 1);
    if (n % 2)
        return matrix_mul(matrix_mul(c, c), m);
    else
        return matrix_mul(c, c);
}

int main()
{
    int n;
    m.v[0][0] = 1, m.v[0][1] = 1;
    m.v[1][0] = 1, m.v[1][1] = 0;
    
    while (scanf("%d", &n) && n != -1)
    {
        if (n == 0) {
            printf("0\n");
            continue;
        }
        Matrix b;
        b = matrix_pow(m, n);
        printf("%d\n", b.v[1][0]);
    }
    return 0;
}