JavaScript – Decimal
前言
之前就写过一篇 decimal, double, float,但写的有点杂乱,这篇把 JS 的部分独立写成一篇整理版。
参考
The Question: 0.1 + 0.2 = ?
JS 有一道经典的问题
console.log(0.1 + 0.2); // 0.30000000000000004
第一次接触 JS 的人可能会感到不可思议,但其实上面这道题,并不是 JS 独有的。
C# 也是一样的计算结果
public class Program { public static void Main() { double x = 0.1; double y = 0.2; double z = x + y; // 0.30000000000000004 } }
Why 0.30...4 ?
代码上看,写的是十进制,但电脑在存储和计算时,其实用的是二进制 (想要深入理解,可以看这篇,我只懂个大概而已)。
0.1 + 0.2,电脑会先把 0.1 转换成二进制,而这个二进制是个无穷数 0.0001100110011001...(无限),所以只能保留一部分的精度 (IEEE 754 标准的 64 位双精度浮点数的小数部分最多支持 53 位二进制位)。
最终相加以后再转换成十进制,精度就丢失了,结果就会有偏差。

图片来源:关于JavaScript中计算精度丢失的问题(一)
toFixed 也有问题
不仅仅是加减乘除,就连 rounding 也是会出错的。
console.log(162.125.toFixed(2)); // 162.13 (四舍五入) console.log(162.295.toFixed(2)); // 162.29 (四舍五入 失败)
先转换成整数,再做计算
可能我们会误以为,只要先把小数转换成整数,然后才做计算,就可以避开精度丢失问题...没有这么简单。
console.log(162.315.toFixed(2)); // 错误 162.31 console.log(Math.round(162.315 * 100) / 100); // 正确 162.32 console.log(Math.round(162.295 * 100) / 100); // 依然错误 162.29
因为 * 100 也是走二进制,所以依然有丢失的可能。
The Answer
上面说了这道题在 C# 也是同样的计算结果,但为什么往往叫的人都是 jser 呢?
因为 C# 有一个 best practice -- 但凡可能会让人计算的数,请使用 decimal。
public class Program { public static void Main() { decimal x = 0.1m; decimal y = 0.2m; decimal z = x + y; // 0.3 } }
换成 decimal 计算就正确了。
decimal vs double
decimal 的特色就是精度准、计算速度慢(因为 CPU 不支持 decimal 计算)、存储空间大、数目小。
所以如果不 care 精准度的话,大部分情况都会使用 double。(比如做游戏啦、科学啦、这些场景一般上需要计算的快、数目又大,但通常不需要太准)
算钱则一定是用 decimal 的,因为要准嘛。
How it work?
为什么 decimal 就 ok 了呢?
因为 decimal 不使用二进制 (这也是它慢的主要原因)。
上面我们提到,精度丢失就是因为十进制转二进制后,变成无穷数,只能存储一部分,而丢失的那部分就不可能还原了,最后就有微差。
decimal 不转二进制,就没有丢失的问题了。
但...不转二进制要怎样计算呢?
C# Decimal 我不清楚。
JS Decimal -- big.js 库的实现方式,就类似于,我们小时候用纸笔做算数那样

import Big from 'big.js'; const n1 = new Big(8881.12); const n2 = new Big(165.26); console.log(n1.plus(n2).toNumber()); // 正确 9046.38 console.log(8881.12 + 165.26); // 错误 9046.380000000001
首先它把 number 转成 string,接着 split,然后按位置保存
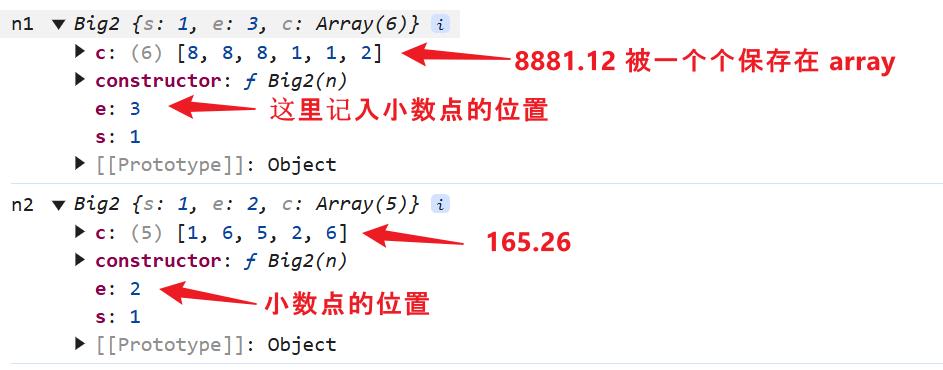
最后按位置做加法计算,进位。

2 + 6 = 8,
1 + 2 = 3,
1 + 5 = 6,
8 + 6 = 14,保留 4,进位 1
8 + 1 + 1 = 10,保留 0,进位 1
8 + 1 = 9
答案倒着看:9046.38
注:这个例子刚巧两个数目的小数点位置是相同的,假如不相同,那在计算之前先对齐就可以了。
由于是挨个挨个位置做加法计算,计算时虽然也会转成二进制,但它每个位置都是整数 (整数转二进制是不会无穷的),不是小数,所以就彻底避开了精度丢失的问题。
当然,这个加法计算,肯定是慢的,要 for loop,要自己处理进位等等一系列繁琐的操作,但视乎也没其它的办法了。
JS Decimal の big.js 库
JS 没有原生的 decimal 类型 (tc39 proposal),但是有 library 可以实现 decimal 的效果。
big.js, bignumber.js, decimal.js 这 3 个库都是同一个作者。
big.js 最轻,也是我目前用着的,三者之间的区别可以看这篇: What is the difference between big.js, bignumber.js and decimal.js? 或它的翻译篇
安装yarn add big.js
yarn add @types/big.js --dev
使用
import Big from 'big.js'; console.log(Big(0.1).plus(0.2).toNumber()); // 0.3
第一步是把 number 变成 Big 对象.
Big(0.1) 或者 new Big(0.1) 都可以, new 是 optional 的.
接着就是调用各做 operator 方法. 比如 plus, minus, mul / times, div (加减乘除, 注: mul 和 times 都是乘, alias 而已)
最后通过 toNumber 把 Big 对象转换成 JS 的 number 类型.
除了加减乘除, big js 也提供了许多对比方法, ===, >, >=, <, <= 等等. 这样写起来就比较方便了.

big.js 没有提供 min、max、sum 这些功能,需要的话得用 reduce 自己累加实现。
toPrecision() 类似 JS 的 toFixed 返回 string
round() 类似 Math.round 但它支持 round to n decimal point,而且有不同的 rounding mode,默认是四舍五入。

JS Workaround (Number.EPSILON)
如果不想大费周章搞 decimal,也可以用一些小技巧解决。
const value = 0.1 + 0.2; if (value === 0.3) { console.log('yes'); } else { console.log('no'); // will be no, because it is 0.30000000000000004 }
把 if expression 换成
const value = 0.1 + 0.2; if (0.3 - value < Number.EPSILON) { // EPSILON is a very very small number 2.220446049250313e-16 console.log('yes'); // will be yes } else { console.log('no'); }
Number.EPSILON 是 es6 的新特性。




