【杂学】先进的 NLP 技术 —— 旋转位置编码（Rotary Position Embedding，RoPE）

Transformer 已经渐渐成为目前 LLM 最通用底层架构之一，其中的位置编码也显得极其重要，由于注意力分数本质上是每个 token 的 val 加权和，并没有考虑其中的空间信息，因此需要在自注意力模块之前就将位置信息融合进序列中。

绝对位置编码

绝对位置编码是一种将序列中的每个位置进行编码的方法，它为每个位置分配一个唯一的编码向量。其优势在于它不依赖于序列中的其他元素，可以独立地表示每个位置的信息，比较简单容易计算。

Transformer 所用的就是绝对位置编码策略，计算公式如下：

$$\text{PE}(pos,2i)=\sin (pos/{10000}^{2i/d})$$

$$\text{PE}(pos,2i+1)=\cos (pos/{10000}^{2i/d})$$

其缺点也比较明显：

1. 绝对位置编码无法反应不同词之间的相对关系，例如位置 1 和 2 跟 5 和 500 的差异是一样的
2. 表示不了比预训练文本长度更长的位置向量表示，如果预训练最大长度为 512 的话，那么最多就只能处理长度为 512 的句子，再长就处理不了了

相对位置编码

相对位置编码不是关注词在句子中的绝对位置，而是关注词和词之间的距离。该方法不会直接向词向量添加位置向量。而是改变了注意力机制以纳入相对位置信息。
比较经典的是 T5 模型中所用的相对位置编码。具体来说，T5 并没有像 Transformer 一样使用 PE，而是在第一个 encoder 的 $Q{K}^T$ 后（soflmax 之后）加入了一个 relative position embbedding：

$${\hat{e}}_{ij}^h=e_{ij}^h+r_{ij}$$

而其中的 $r$ 是一个标量，共有 32 种取值。这 32 种取值进行分配的策略基于假设：位置离得近的更需要精细的编码，而比较远的相反。例如设 $i,j$ 分别为两个词的位置，$i-j$ 在 $[-5,5]$ 会使用 5 种编码，而在 $[32,64]$ 区间用的都是同一种编码。

相对位置编码的缺点有：

1. 增添了计算量，需要额外维护 $r$ 矩阵
2. 无法适用于 KV-cache 技术。使用 KV-cache 的一项要求是已经生成的单词的位置编码，在生成新单词时不改变，而相对位置编码会变化

旋转位置编码

如上所述，相对或绝对位置编码均有其局限性。旋转位置编码（RoPE）是一种全新的方法，巧妙地融合了传统方法的优点。

二维

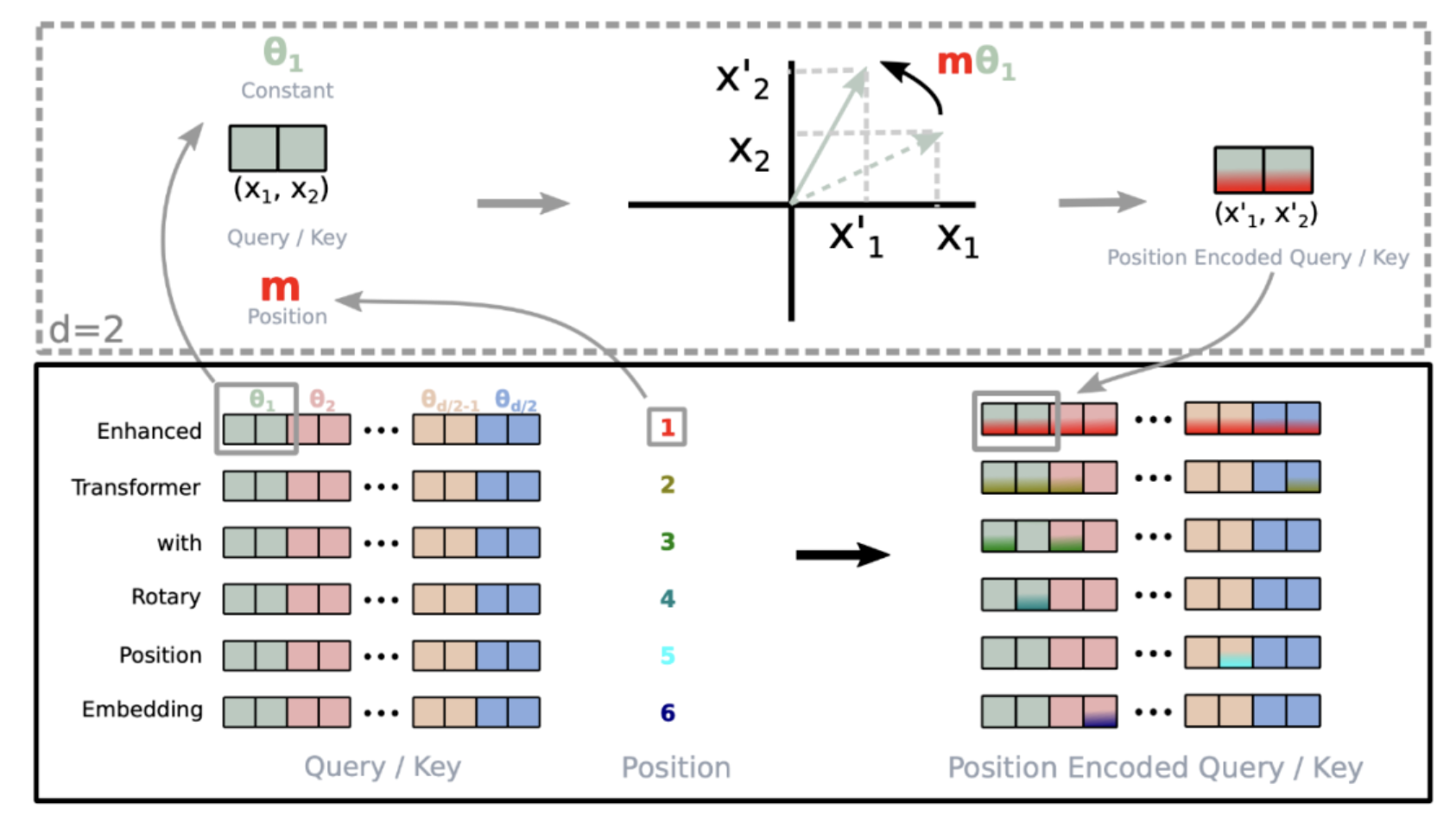
二维的旋转位置编码可以理解为在二维平面上将不同的 token 进行不同角度的旋转。计算公式可以推导为如下形式：

$$\begin{array}{rl}{f}_k({\mathit{x}}_m,m)& =(\begin{array}{cc}\cos m\theta & -\sin m\theta )\\ \sin m\theta & \cos m\theta \end{array})\left(\begin{array}{cc}{W}_k^{(1,1)}& W_k^{(1,2)}\\ W_k^{(2,1)}& W_k^{(2,2)}\end{array}\right)\left(\begin{array}{c}{x}_m^{(1)}\\ x_m^{(2)}\end{array}\right)\\ & =\left(\begin{array}{cc}\cos m\theta & -\sin m\theta )\\ \sin m\theta & \cos m\theta \end{array}\right)\left(\begin{array}{c}{k}_m^{(1)}\\ k_m^{(2)}\end{array}\right)\end{array}$$

其中 $f_q$ 为加入位置编码的 $q$ 向量。同样可以定义 $f_k$，进一步可以求得两个矩阵的内积：

$$g({\mathit{x}}_m,{\mathit{x}}_n,m-n)=\left(\begin{array}{cc}{\mathit{q}}_m^{(1)}& {\mathit{q}}_m^{(2)}\end{array}\right)\left(\begin{array}{cc}\cos ((m-n)\theta )& -\sin ((m-n)\theta )\\ \sin ((m-n)\theta )& \cos ((m-n)\theta )\end{array}\right)\left(\begin{array}{c}{k}_n^{(1)}\\ k_n^{(2)}\end{array}\right)$$

扩展到多维

由于内积满足线性叠加性，因此对于偶数维度的 RoPE，我们可以基于二维进行叠加扩展：

$${\mathit{R}}_{\mathrm{\Theta },m}^d=\underset{{\mathit{W}}_m}{\underbrace{\left(\begin{array}{ccccccc}\cos m{\theta }_0& -\sin m{\theta }_0& 0& 0& \cdots & 0& 0\\ \sin m{\theta }_0& \cos m{\theta }_0& 0& 0& \cdots & 0& 0\\ 0& 0& \cos m{\theta }_1& -\sin m{\theta }_1& \cdots & 0& 0\\ 0& 0& \sin m{\theta }_1& \cos m{\theta }_1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& 0& \cdots & \cos m{\theta }_{d/2-1}& -\sin m{\theta }_{d/2-1}\\ 0& 0& 0& 0& \cdots & \sin m{\theta }_{d/2-1}& \cos m{\theta }_{d/2-1}\end{array}\right)}}$$

$$\mathrm{\Theta }=\{{\theta }_i={10000}^{-2(i-1)/d},i\in [1,2,\dots ,d/2]\}$$

总结

RoPE 不仅解决了输入文本过长之后引起的上下文无法关联问题，并且还提高了训练和推理的速度。总的来说，RoPE 的 self-attention 操作的流程是：

1. 对于 token 序列中的每个词嵌入向量，首先计算其对应的 query 和 key 向量
2. 对每个 token 位置都计算对应的旋转位置编码
3. 接着对每个 token 位置的 query 和 key 向量的元素按照两两一组应用旋转变换
4. 最后再计算 query 和 key 之间的内积得到 self-attention 的计算结果。