【论文阅读笔记】大模型微调 —— LoRA

论文地址：https://arxiv.org/pdf/2106.09685
代码地址：https://github.com/microsoft/LoRA

image

简介

GPT-3、BERT 以来，预训练+微调渐渐成为大预言模型的新范式；而在微调阶段，如何能找到一个非常高效且效果很好的方法成为了研究热点，一个相关的 topic 就是 Parameter Efficient Fine-Tuning(PEFT)。本文以此为出发点探究了大模型微调的方法，发现目前的微调方法，如 adapter 会更改模型架构，从而带来推理延迟。
image

作者从 Li et al [1] 和 Aghajanyan et al [2] 处获得灵感：学习到的过度参数化模型实际上存在于低内在维上，即微调阶段实际在调整的只有低维的某些参数。由此，作者假设设模型适应过程中的权重变化也具有较低的“内在秩”，提出了 Low-Rank Adaptation(LoRA) 方法，将参数分解为低秩矩阵，从而大大降低训练的复杂度。

论文在很多数据集上做了实验，证明 LoRA 方法存在的道理以及其有效性。

方法

问题定义

一般微调可以定义为如下形式：

\[\max_{\Phi}\sum_{(x,y)\in\mathcal{Z}}\sum_{t=1}^{|y|}\log\left(P_{\Phi}(y_t|x,y_{<t})\right) \]

其中 \(P_{\Phi}\) 为模型，\(\mathcal{Z}=\{(x_{i},y_{i})\}_{i=1,..,N}\) 为数据集，利用对数似然不断优化模型。在实际的 LLM 中，\(|{\Phi}|\) 可能非常大，如 GPT-3 中会达到 175B，本文作者将上述定义改写为如下形式：

\[\max_{\Theta}\sum_{(x,y)\in\mathcal{Z}}\sum_{t=1}^{|y|}\log\left(p_{\Phi_0+\Delta\Phi(\Theta)}(y_t|x,y_{<t})\right) \]

其中 \(\Delta\Phi(\Theta)\) 是低秩的。

具体实现

进一步，作者提出了如下矩阵分解：
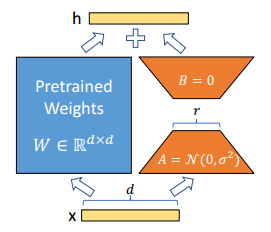
image
形式化来讲如下公式，其中 \(W_0\) 被冻结，不接受梯度更新，而 \(A\) 和 \(B\) 包含可训练参数，其维度为 \(d \times r\) 和 \(r \times d\)，秩为 \(r\)。

\[h=W_0x+\Delta Wx=W_0x+BAx \]

在一开始，\(A\) 使用随机高斯初始化，\(B\) 初始化为0，这样使 \(\Delta W = BA = 0\)。再将 \(\Delta W\) 乘以一个缩放因子 \(\frac{\alpha}{r}\)，其中 \(\alpha\) 固定为第一次尝试的 \(r\) 即可。

在 Transformer 应用

本文主要探讨了将 LoRA 应用于自注意力块 (\(W_q, W_k, W_v, W_o\))，并将 MLP 的 LoRA 微调留给了 future work。在这里，我们首先假设 \(W_q, W_k, W_v\) 维度均为 \(d_{model} \times d_{model}\)，在 \(r << d_{model}\) 的情况下（\(r = 1, 2, 4\)）：

  • 训练参数由 \(d_{model}^2\) 缩减为 \(rd_{model}\)；
  • VRAM 的使用可以减少 \(2/3\)；
  • checkpoint 大小减少了约 10000 倍（\(r = 4\)）
  • 在GPT-3 175B的训练过程中，与完全微调相比，速度提高了25%

实验

Baseline

  • Bias-only or BitFit：只训练偏移量。
  • Prefix-embedding tuning (PreEmbed)：嵌入层插入特殊的 tokens，参数量 \(|\Theta|=d_{model}\times(l_{p}+l_{i})\)，\(l_p\) 和 \(l_i\) 分别为前缀和中缀长度。
  • Prefix-layer tuning (PreLayer)：不止学习嵌入层，将激活层也被替换为科学系的激活，参数量 \(|\Theta|=L \times d_{model}\times(l_{p}+l_{i})\)，\(L\) 为激活层数量。
  • Adapter tuning：在自注意力块或 MLP 连接处增加 adapter，参数量 \(|\Theta|=\hat{L}_{Adpt}\times(2\times d_{model}\times r+r+d_{model})+2\times\hat{L}_{LN}\times d_{model}\)，其中 \(\hat{L}_{Adpt}\) 为可训练的 adapter 数量，\(\hat{L}_{LN}\) 为 LayerNorm 层的数量。

RoBERT 模型

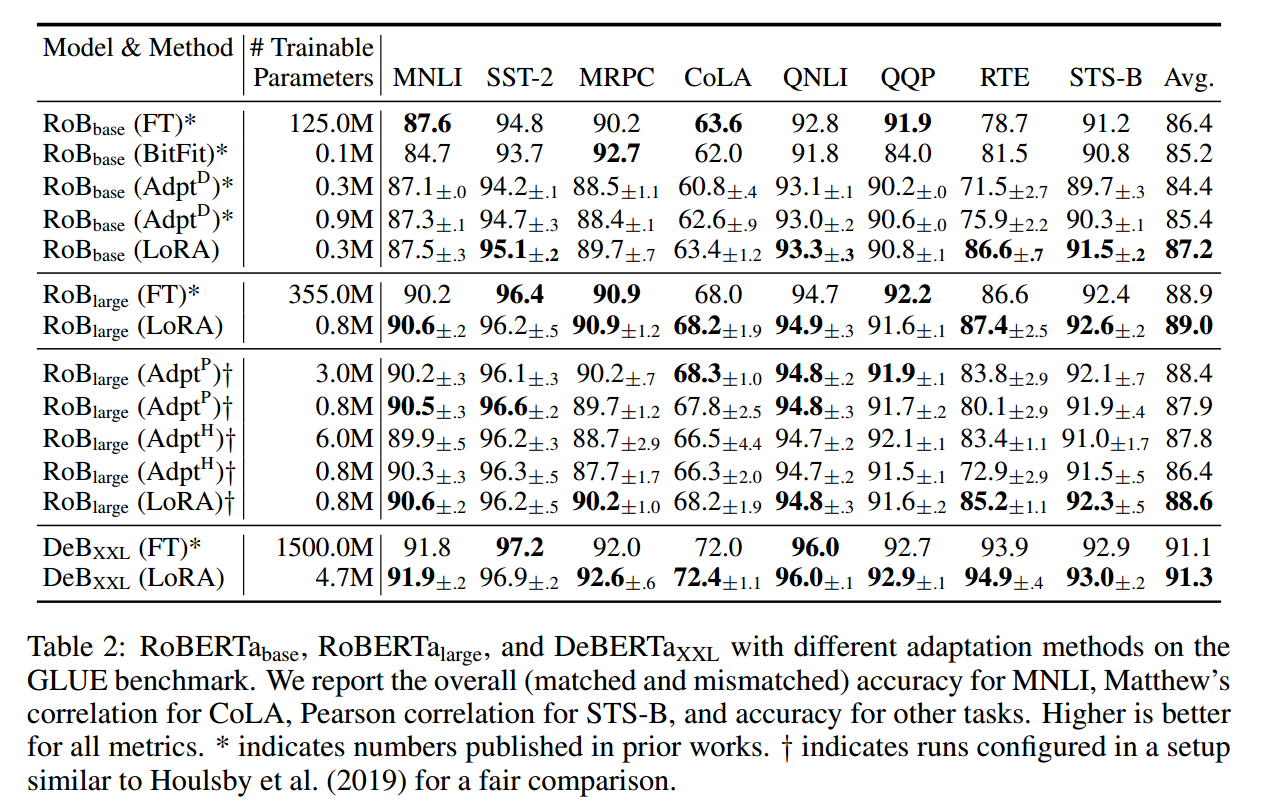
image

GPT-2 模型

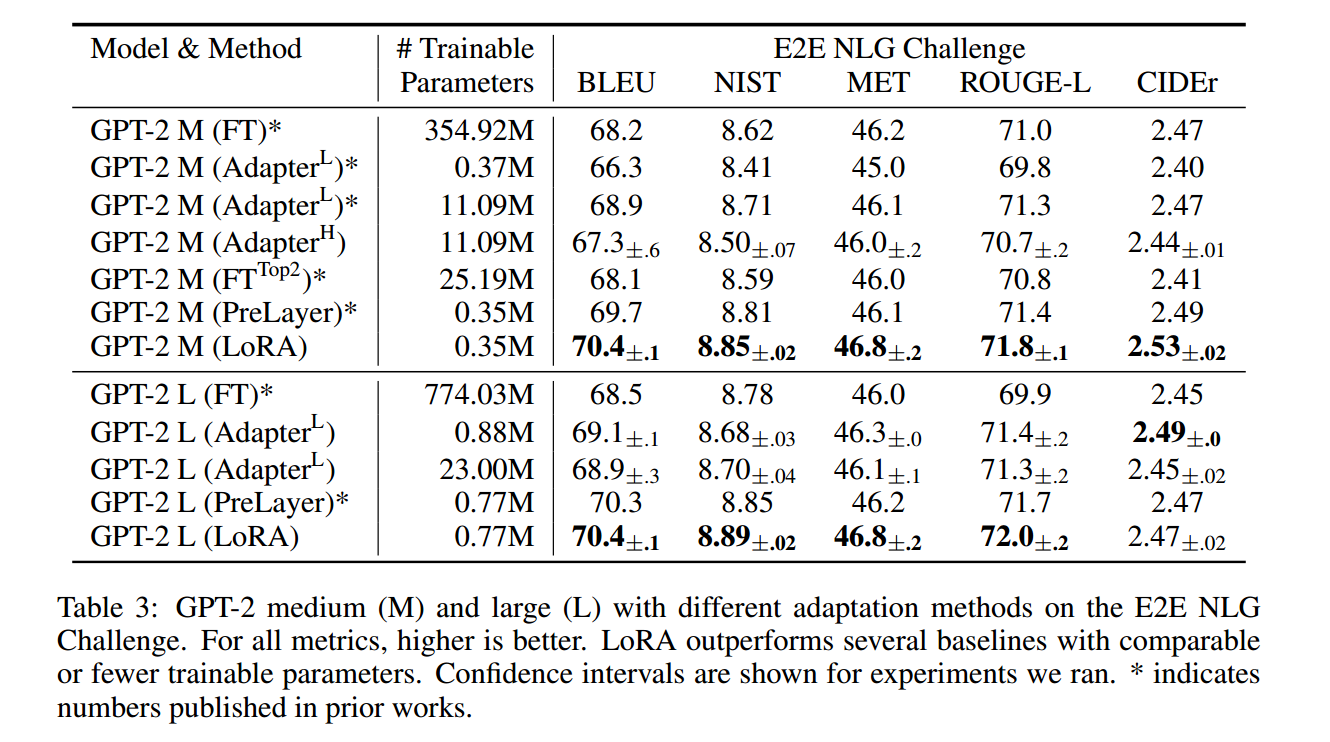
image

GPT-3 模型

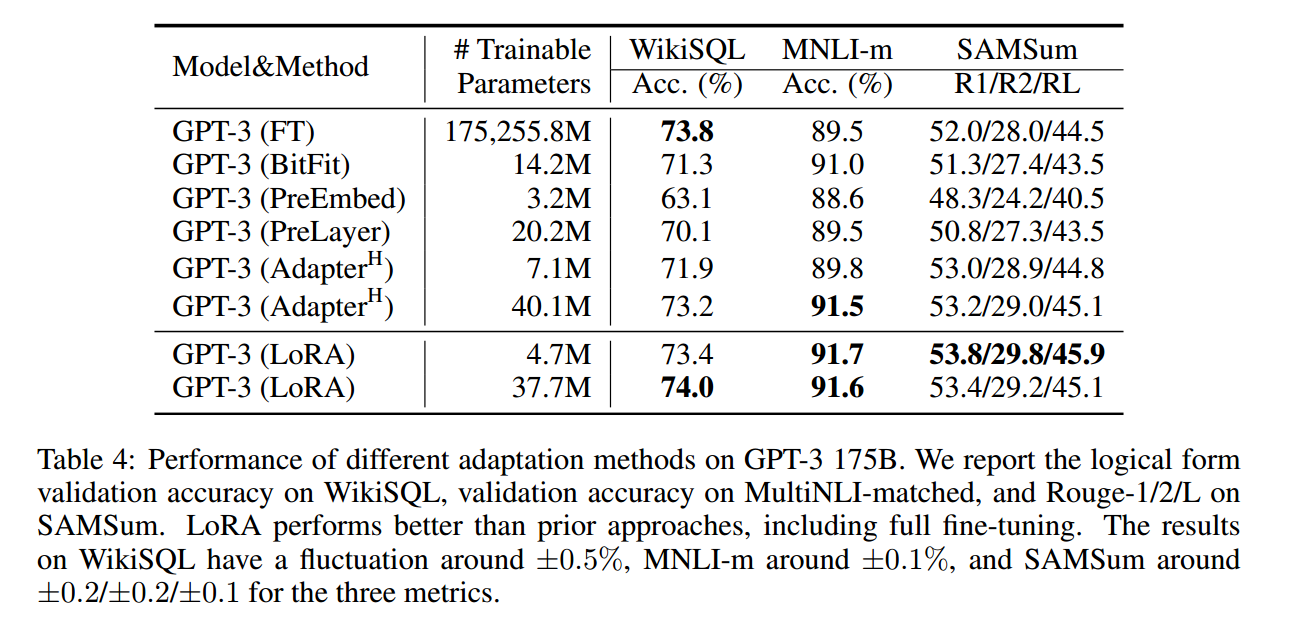
image

讨论

个人认为本篇的精髓所在，能够引用5k+的原因之一

应用到 Transformer 哪里？

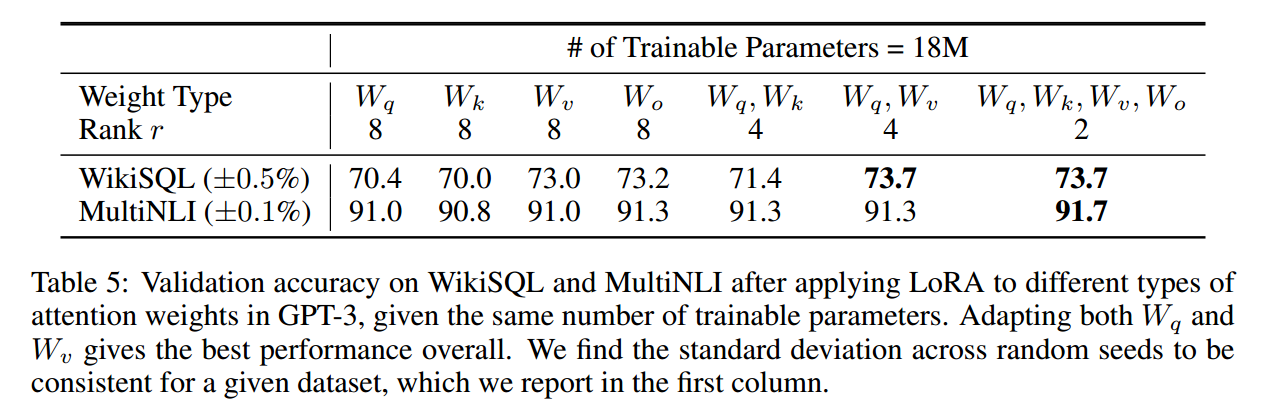
image
更低的秩有可能导致更好的效果。

最好的 \(r\) 是多少？

为了探究这一问题，作者首先利用不同的 \(r\) 进行实验，结果如下图所示：
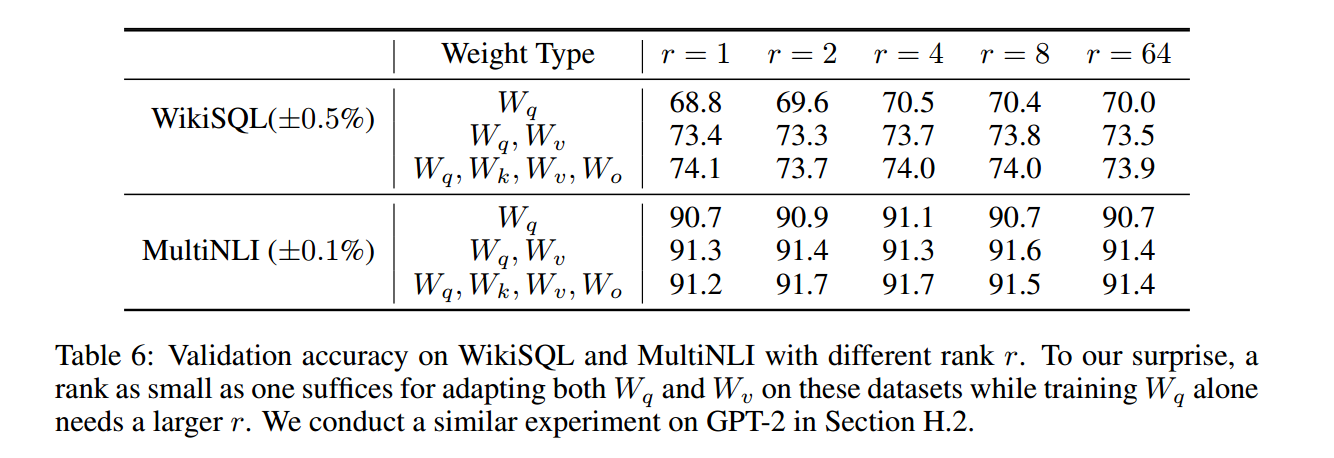
image
可以看到 \(r\) 很低地时候模型效果已经相当不错，为什么导致这一现象呢？作者做了如下的实验进行解释：
对于 \(A_{r=8}\) 和 \(A_{r=64}\) 分别为秩等于 8 和 64 的矩阵 \(A\)，利用奇异值分解得到右奇异酉矩阵 \(U_{A_{r=8}}\) 和 \(U_{A_{r=8}}\)。那么我们希望知道，\(U_{A_{r=8}}(1≤i≤8)\) 中由前 \(i\) 个奇异向量张成的子空间中有多少包含在 \(U_{A_{r=8}}(1≤j≤64)\) 中由前 \(j\) 个奇异向量张成的子空间中？因此定义如下的基于 Grassmann 距离的标准化子空间相似性：

\[\phi(A_{r=8},A_{r=64},i,j)=\frac{||U_{A_{r=8}}^{i\top}U_{A_{r=64}}^j||_F^2}{\min(i,j)}\in[0,1] \]

\(\phi(·)\) 取值为 0 时表示子空间完全不重叠，1 表示完全重叠；对于不同的 \(i\) 和 \(j\) 可以画出如下的图：
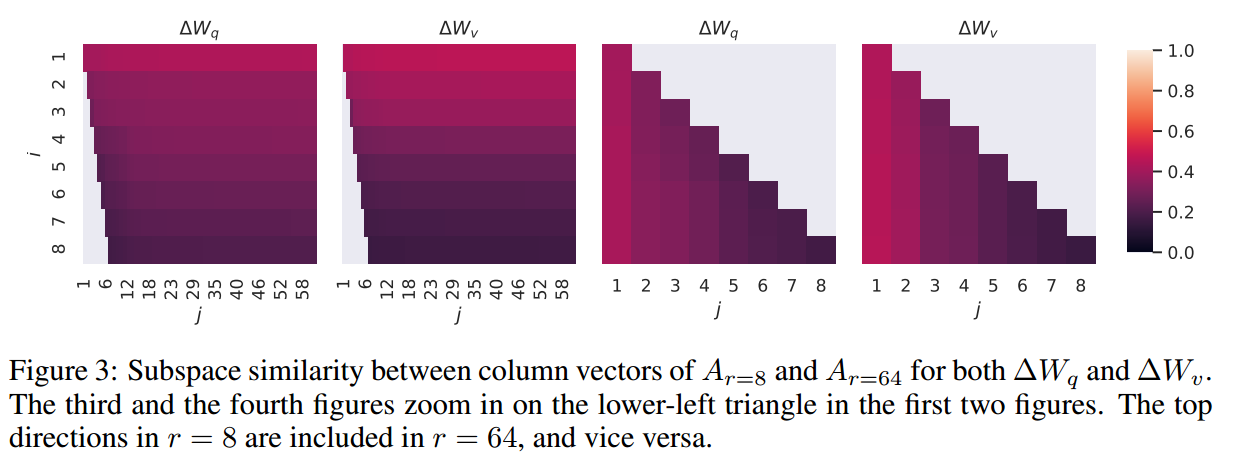
image
这说明了不同的 \(A\) 也会在第一维上共享子空间，证明了为什么 \(r=1\) 也能在 GPT-3 上取得很好的效果。

\(\Delta W\) 和 \(W\) 有什么关系吗？

作者进一步思考了 \(\Delta W\) 和 \(W\) 两者的关系，同样的，利用奇异值分解 + F-范数进行计算可以得到如下结果：
image

  • 首先，与随机矩阵相比，\(∆W\) 与 \(W\) 的相关性更强，说明 \(∆W\) 放大了 \(W\) 中已经存在的一些特征（下图）。
  • 其次，\(∆W\) 并没有重复W的最上面的奇异方向，而是只放大了 \(W\) 中没有强调的方向。
  • 第三，放大系数非常大：当 \(r = 4\) 时，其放大系数为 \(21.5≈6.91/0.32\)。
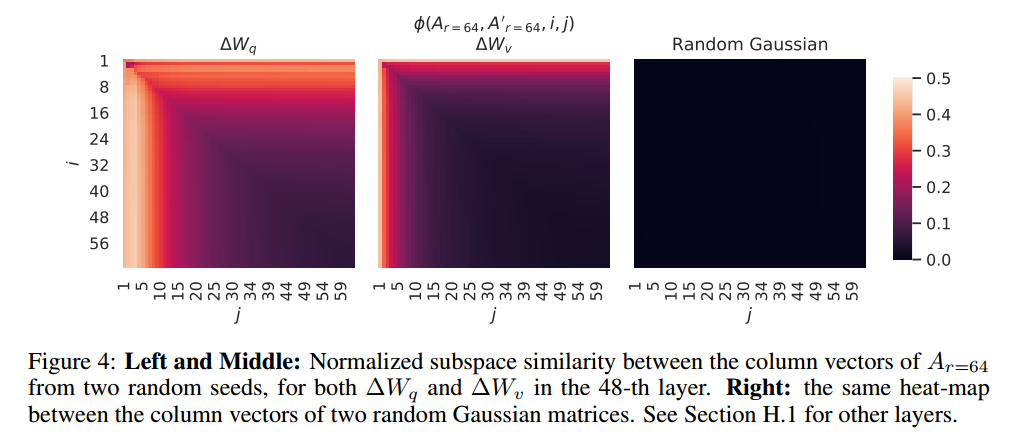
    image

感想

论文方法不难，不涉及复杂的数学原理和模型架构，但是可以对后面的PEFT领域起到很关键的作用，也可以算是里程碑式的作品了；个人认为是其巧妙的idea和论文中完备的实验：

  1. 从 idea 来看，作者第一次在不改变模型架构的基础上进行微调，可以说是开创了一个全新的 PEFT 方法，作者也在文章里挖了很多坑，使得这一算法被后续多次改进；
  2. 作者通过较长篇幅的讨论来验证他们的方法有效性以及可解释性，使得玄学的神经网络能够用数学严谨地证明。

Reference

  1. Chunyuan Li, Heerad Farkhoor, Rosanne Liu, and Jason Yosinski. Measuring the Intrinsic Dimension of Objective Landscapes. arXiv:1804.08838 [cs, stat], April 2018a. URL http://arxiv.org/abs/1804.08838. arXiv: 1804.08838. ↩︎

  2. Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta. Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning. arXiv:2012.13255 [cs], December 2020. URL http://arxiv.org/abs/2012.13255. ↩︎

posted @ 2024-07-21 12:27  KeanShi  阅读(308)  评论(0)  编辑  收藏  举报