【题解】HDOJ 7293 [2023杭电多校] foreverlasting and fried-chicken
题目传送门:HDOJ 7293 [2023杭电多校] foreverlasting and fried-chicken
题意
给一个 \(n\) 个节点的图,找出如下形式的子图有多少个
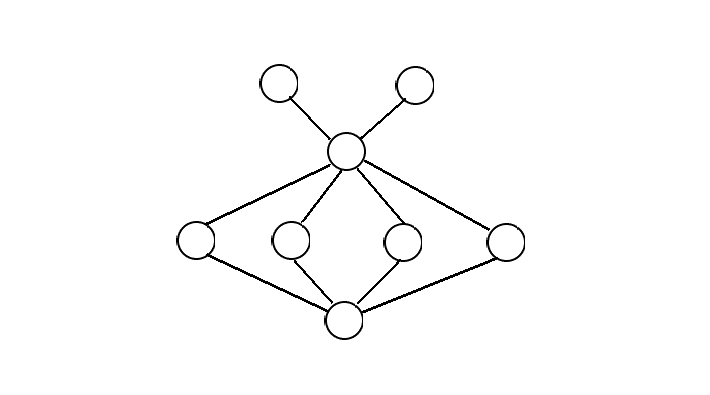
其中 \(n \le 1000\),结果模 \(1e9 + 7\)
分析
可以发现关键就是中间那个度数为6的点,暴力枚举即可,数据量允许 \(O(n^2)\) 的算法,难点在于找到距离为2的点有哪些,并且长度为2的路有几条,这里考虑使用bitset优化
题解
使用bitset存图,(bt[i] & bt[j]).count() 即为 \(i\) 和 \(j\) 点之间有多少距离为2的路;然后暴力求组合数就行,注意这里有个wa点:中心点和最下面的点可能也有一条边相连,因此在枚举上面两个孤立的节点时候记得去掉最下面的点
AC代码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define int long long
#define cin std::cin
#define cout std::cout
#define fastio ios::sync_with_stdio(0), cin.tie(nullptr)
using namespace std;
const int N = 1e3 + 10;
const int mod = 1e9 + 7;
const int inf = 0x3fffffffffffffff;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){
return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;
}
inline int read(){
int ret = 0,f = 0;char ch = getc();
while (!isdigit (ch)){
if (ch == '-') f = 1;
ch = getc();
}
while (isdigit (ch)){
ret = ret * 10 + ch - 48;
ch = getc();
}
return f?-ret:ret;
}
int frac[N], inv[N];
// 快速幂
int qpow(int a, int b) {
a %= mod;
int s = 1;
for (; b; a = 1ll * a * a % mod, b >>= 1) if (b & 1) s = 1ll * s * a % mod;
return s;
}
// 线性求逆元
void set_up() {
frac[0] = inv[0] = 1;
for (int i = 1; i <= N - 1; i++) frac[i] = 1ll * frac[i - 1] * i % mod;
inv[N - 1] = qpow(frac[N - 1], mod - 2);
for (int i = N - 2; i; i--) inv[i] = 1ll * inv[i + 1] * (i + 1) % mod;
}
// O(1)计算组合数
inline int C(int n, int m) {
if (n < m) return 0;
return (1ll * frac[n] % mod * inv[m] % mod * inv[n - m] % mod) % mod;
}
int n, m;
int cnt[N][N], deg[N];
bitset<1005> bt[N];
inline void solve() {
int ans = 0;
n = read(), m = read();
for(int i = 1; i <= n; ++i) {
deg[i] = 0;
bt[i].reset();
for(int j = 1; j <= n; ++j) {
cnt[i][j] = 0;
}
}
for(int i = 1; i <= m; ++i) {
int s, t;
s = read();
t = read();
bt[s][t] = 1;
bt[t][s] = 1;
deg[s] ++;
deg[t] ++;
}
for(int i = 1; i <= n; ++i) {
for(int j = i + 1; j <= n; ++j) {
int num = (bt[i] & bt[j]).count();
cnt[i][j] += num;
cnt[j][i] += num;
}
}
for(int i = 1; i <= n; ++i) {
if(deg[i] < 6) continue;
int num = 0;
for(int j = 1; j <= n; ++j) {
ans = (ans + 1ll * C(cnt[i][j], 4) % mod * C(deg[i] - bt[i][j] - 4, 2) % mod) % mod;
}
}
printf("%lld\n", ans % mod);
}
signed main() {
fastio;
int T;
T = read();
set_up();
while(T --) {
solve();
}
return 0;
}


